Числовые и функциональные ряды
Числовые и функциональные ряды
Числовой ряд. Основные понятия. Знакоположительные ряды
Примеры решения типовых задач
Пример 1. Найти сумму ряда 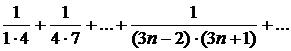 .
.
Решение. Составим частичную сумму:
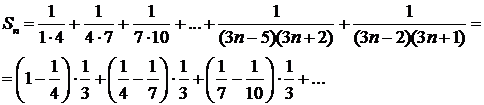
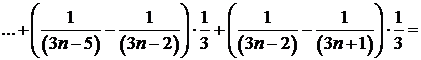
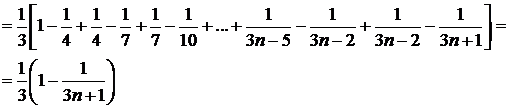
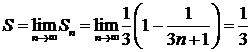 .
.
Пример 2. Найти сумму ряда 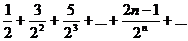
Решение. Составим последовательность частичных сумм:
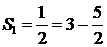 ,
,
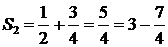 ,
,
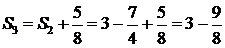 .
.
Если 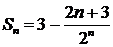 , то
, то 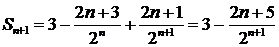 .
.
Следовательно, 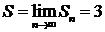 .
.
Пример 3. Найти сумму ряда 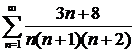 .
.
Решение. Представим общий член ряда в виде суммы простейших дробей:
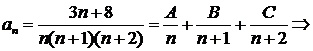
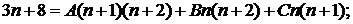
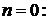
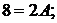
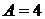
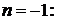
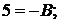
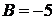
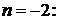
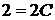 ;
; 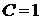
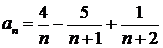
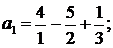
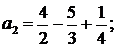
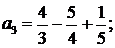
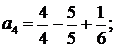
………………
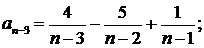
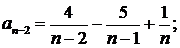
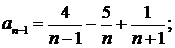
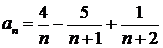 ;
;
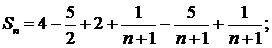
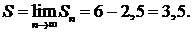
Пример 4.Исследовать на сходимость ряд 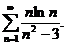
Решение. Проверим выполнение необходимого условия 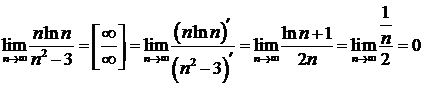 . Необходимое условие выполняется, однако, это не означает, что ряд сходится. Исследуем на сходимость с помощью достаточных признаков. Этот ряд можно исследовать на сходимость с помощью признака сравнения. Сравним исследуемый ряд с гармоническим рядом
. Необходимое условие выполняется, однако, это не означает, что ряд сходится. Исследуем на сходимость с помощью достаточных признаков. Этот ряд можно исследовать на сходимость с помощью признака сравнения. Сравним исследуемый ряд с гармоническим рядом 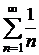 . Начиная с
. Начиная с 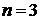 члены нашего ряда больше соответствующих членов гармонического ряда
члены нашего ряда больше соответствующих членов гармонического ряда
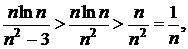 так как при
так как при 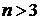 ,
, 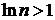 . Гармонический ряд расходится, следовательно, расходится и ряд
. Гармонический ряд расходится, следовательно, расходится и ряд 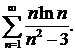
Пример 5.Исследовать на сходимость ряд 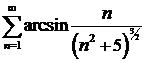 .
.
Решение. 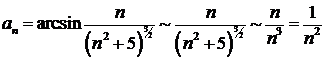 при
при 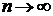 . Ряд
. Ряд 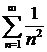 – обобщенный гармонический ряд с показателем
– обобщенный гармонический ряд с показателем 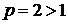 сходится. Значит, данный ряд
сходится. Значит, данный ряд 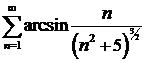 , члены которого эквивалентны членам обобщенного гармонического ряда, сходится.
, члены которого эквивалентны членам обобщенного гармонического ряда, сходится.
Пример 6. Исследовать на сходимость ряд 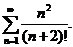
Решение. Используем признак Даламбера. Имеем :
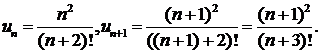
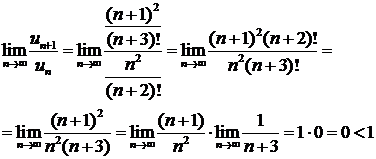
Следовательно, исследуемый ряд сходится.
Пример 7.Исследовать на сходимость ряд 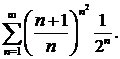
Решение. Здесь удобно применить признак Коши. 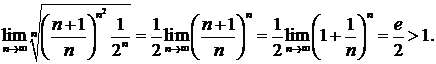 Следовательно, ряд
Следовательно, ряд 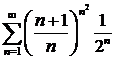 расходится.
расходится.
Пример 8. Исследовать на сходимость ряд 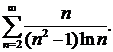
Решение.Воспользуемся предельным признаком сравнения. Вместо ряда 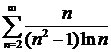 можно исследовать на сходимость более простой ряд
можно исследовать на сходимость более простой ряд 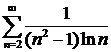 , так как
, так как 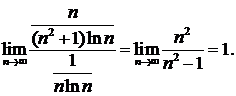 Применим интегральный признак сходимости ряда. Вычислим несобственный интеграл от функции
Применим интегральный признак сходимости ряда. Вычислим несобственный интеграл от функции 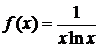 , удовлетворяющей условиям интегрального признака.
, удовлетворяющей условиям интегрального признака.
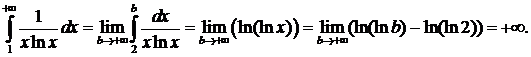
Интеграл расходится, значит будет расходится и ряд.
Пример 9. Доказать справедливость равенства 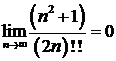 .
.
Решение. Рассмотрим ряд 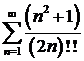 . Исследуем его сходимость по признаку Даламбера:
. Исследуем его сходимость по признаку Даламбера:
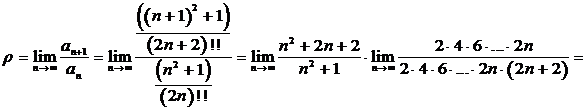
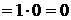
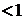 .
.
Ряд сходится. Следовательно, по необходимому признаку предел общего члена равен нулю.
Задания для самостоятельной работы
10.1. Доказать сходимость ряда и найти его сумму:
а) 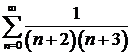 ; ; | б) 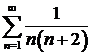 ; ; |
в) 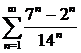 ; ; | г) 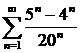 ; ; |
д) 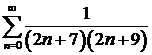 ; ; | е) 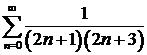 ; ; |
ж) 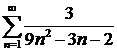 ; ; | з) 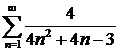 . . |
10.2. Исследовать сходимость ряда с помощью одного из признаков сравнения:
а) 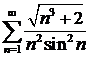 ; ; | б) 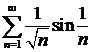 ; ; |
в) 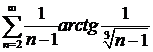 ; ; | г) 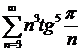 ; ; |
д) 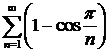 ; ; | е) 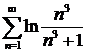 ; ; |
ж) 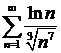 ; ; | з) 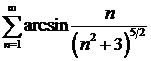 . . |
10.3. Исследовать сходимость ряда с помощью признака Даламбера:
а) 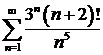 ; ; | б) 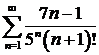 ; ; |
в) 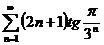 ; ; | г) 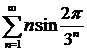 ; ; |
д) 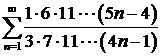 ; ; | е) 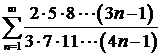 ; ; |
ж) 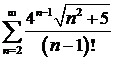 ; ; | з) 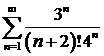 . . |
10.4. Исследовать сходимость ряда с помощью радикального признака Коши:
а) 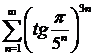 ; ; | б) 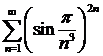 ; ; |
в) 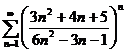 ; ; | г) 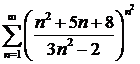 ; ; |
д) 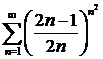 ; ; | е) 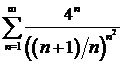 ; ; |
ж) 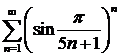 ; ; | з) 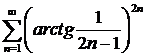 . . |
10.5. Исследовать сходимость ряда с помощью интегрального признака Коши:
а) 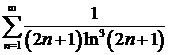 ; ; | б) 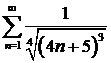 ; ; |
в) 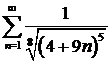 ; ; | г) 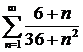 ; ; |
д) 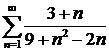 ; ; | е) 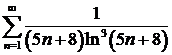 ; ; |
ж) 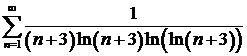 ; ; | з) 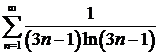 . . |
10.6. Исследовать на сходимость (разные задачи):
а) 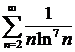 ; ; | б) 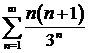 ; ; |
в) 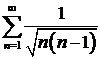 ; ; | г) 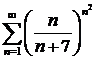 ; ; |
д) 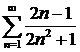 ; ; | е) 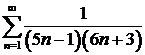 ; ; |
ж) 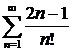 ; ; | з) 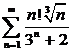 . . |
10.7. Доказать справедливость равенства. (Ответом служит число 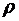 , получаемое при применении признака Даламбера или признака Коши):
, получаемое при применении признака Даламбера или признака Коши):
а); 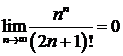 | б) 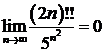 ; ; |
в) 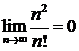 ; ; | г) 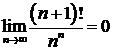 ; ; |
д) 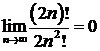 ; ; | е) 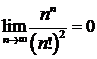 ; ; |
ж) 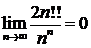 ; ; | з) 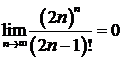 . . |
Ответы
10.1. а) 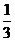 ; б)
; б) 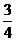 ; в)
; в) 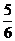 ; г)
; г) 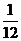 ; д)
; д) 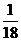 ; е)
; е) 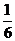 ; ж) 1; з)
; ж) 1; з) 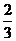 .10.2. а) расходится; б) сходится; в)сходится; г) сходится; д) сходится; е) сходится; ж)расходится; з) сходится. 10.3. а)расходится; б) сходится; в) сходится; г) сходится; д) расходится; е) сходится; ж)сходится; з) сходится. 10.4. а) сходится; б) сходится; в) сходится; г) сходится; д)сходится; е) расходится; ж) сходится; з) сходится. 10.5. а) сходится; б) расходится; в)расходится; г) расходится; д) расходится; е) расходится; ж) расходится; з) расходится. 10.6. а) сходится; б) сходится; в) расходится; г) сходится; д) расходится; е) сходится; ж)сходится; з) расходится.
.10.2. а) расходится; б) сходится; в)сходится; г) сходится; д) сходится; е) сходится; ж)расходится; з) сходится. 10.3. а)расходится; б) сходится; в) сходится; г) сходится; д) расходится; е) сходится; ж)сходится; з) сходится. 10.4. а) сходится; б) сходится; в) сходится; г) сходится; д)сходится; е) расходится; ж) сходится; з) сходится. 10.5. а) сходится; б) расходится; в)расходится; г) расходится; д) расходится; е) расходится; ж) расходится; з) расходится. 10.6. а) сходится; б) сходится; в) расходится; г) сходится; д) расходится; е) сходится; ж)сходится; з) расходится.
Знакопеременные ряды
Примеры решения типовых задач
Пример 1. Исследовать на сходимость ряд 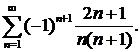
Решение. Этот ряд знакочередующийся. Применим признак Лейбница. Проверим выполнение первого условия.
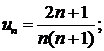
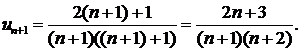
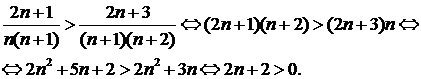
Выполнение второго условия очевидно 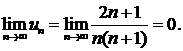
Значит, выполнены оба условия признака Лейбница. Следовательно, данный ряд сходится. Исследуем на сходимость ряд, составленный из абсолютных величин членов первоначального ряда 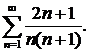 Покажем, что ряд
Покажем, что ряд 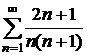 и гармонический ряд ведут себя одинаково.
и гармонический ряд ведут себя одинаково.
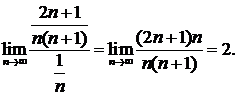 Значит ряд, составленный из абсолютных величин, расходится. Таким образом, что исходный ряд сходится условно.
Значит ряд, составленный из абсолютных величин, расходится. Таким образом, что исходный ряд сходится условно.
Пример 2. Исследовать на сходимость ряд. 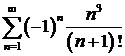 .
.
Решение. В данном примере сначала исследуем знакочередующийся ряд на абсолютную сходимость, т.е. исследуем сходимость ряда, составленного из абсолютных величин членов данного ряда 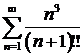 .
.
По признаку Даламбера
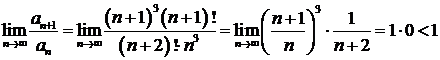 .
.
Ряд из абсолютных величин сходится, следовательно, данный знакочередующийся ряд сходится абсолютно.
Пример 3. Найти сумму ряда 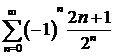 .
.
Решение. Составим последовательность частичных сумм 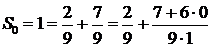 ,
,
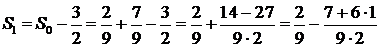 ,
,
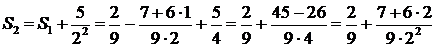 ,
,
т.е. 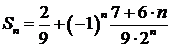 , тогда
, тогда
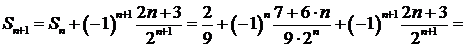
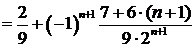 .
.
Следовательно, 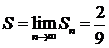 .
.
Пример 4. Сколько членов ряда 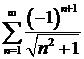 следует взять, чтобы получить сумму ряда с точностью до
следует взять, чтобы получить сумму ряда с точностью до 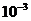 ?
?
Решение. Данный знакочередующийся ряд сходится по признаку Лейбница. Если возьмем 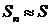 , то ошибка не превосходит
, то ошибка не превосходит 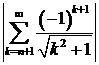 . Но для знакочередующихся рядов остаток ряда по абсолютной величине не превосходит величины своего первого члена, т.е.
. Но для знакочередующихся рядов остаток ряда по абсолютной величине не превосходит величины своего первого члена, т.е. 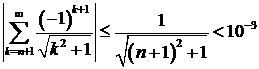 , что верно при
, что верно при 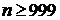 . Отсюда ясно, что достаточно взять 999 членов ряда. Тогда получим требуемую точность.
. Отсюда ясно, что достаточно взять 999 членов ряда. Тогда получим требуемую точность.
Пример 5. Исследовать на сходимость ряд 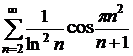 .
.
Решение. 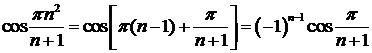 , поэтому данный ряд имеет вид
, поэтому данный ряд имеет вид 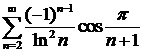 . Но ряд
. Но ряд 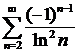 сходится по признаку Лейбница, а
сходится по признаку Лейбница, а 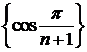 монотонная и ограниченная последовательность. Значит, по признаку Абеля исходный ряд сходится.
монотонная и ограниченная последовательность. Значит, по признаку Абеля исходный ряд сходится.
Рассмотрим ряд из абсолютных величин 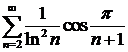 . Так как
. Так как 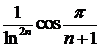 ~
~ 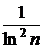 при
при 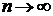 и
и 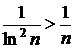 начиная с некоторого n, а
начиная с некоторого n, а 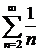 расходится, то
расходится, то 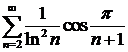 расходится. Значит, данный ряд расходится условно.
расходится. Значит, данный ряд расходится условно.
Пример 6. Вычислить сумму ряда 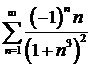 с точностью до
с точностью до 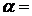 0,001.
0,001.
Решение. Для знакочередующихся рядов погрешность не превышает первого отброшенного члена.
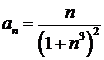 .
.
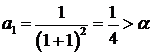 ,
,
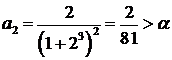 ,
,
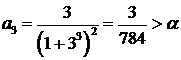 ,
,
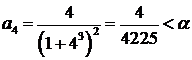 .
.
Поэтому искомая сумма с точностью до 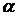 равна
равна
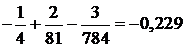 .
.
Задания для самостоятельной работы
10.8. Исследовать ряд на абсолютную и условную сходимость:
а) 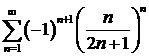 ; ; | б)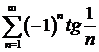 ; ; |
в)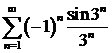 ; ; | г)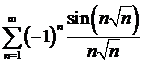 ; ; |
д) 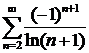 ; ; | е)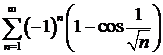 ; ; |
ж) 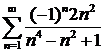 ; ; | з) 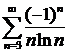 . . |
10.9. Вычислить сумму ряда с точностью 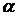 :
:
а) 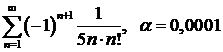 ; ; | б) 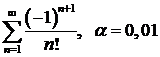 ; ; |
в) 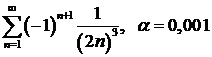 ; ; | г) 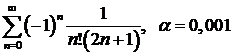 ; ; |
д)  ; ; | е) 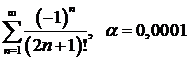 ; ; |
ж) 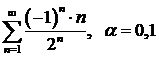 ; ; | з) 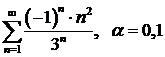 . . |
Ответы
10.8. а) абсолютно сходится; б) сходится условно; в) сходится абсолютно; г) сходится абсолютно; д) сходится условно; е) сходится условно; ж) сходится абсолютно; з) сходится условно. 10.9. а) 0, 18127; б) 0,633; в) 0,112; г) –0,303; з) 0,5.
Функциональные ряды
Примеры решения типовых задач
Пример 1. Найти область сходимости функционального ряда
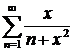 .
.
Решение. При х=0 ряд принимает вид 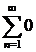 , его частичная сумма
, его частичная сумма 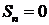 , и, по определению суммы ряда
, и, по определению суммы ряда 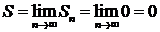 .
.
Пусть 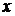 – фиксированное число,
– фиксированное число, 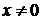 . Исследуем сходимость получившегося числового ряда
. Исследуем сходимость получившегося числового ряда 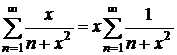 по интегральному признаку Коши:
по интегральному признаку Коши: 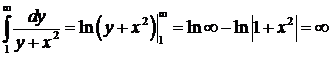 . Интеграл расходится при всех фиксированных значениях
. Интеграл расходится при всех фиксированных значениях 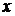 , следовательно, расходится при всех
, следовательно, расходится при всех 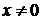 и ряд
и ряд 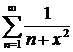 . Данный ряд получается из вспомогательного ряда умножением на число
. Данный ряд получается из вспомогательного ряда умножением на число 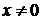 , что не меняет сходимости ряда. Таким образом, область сходимости данного ряда состоит из одной точки
, что не меняет сходимости ряда. Таким образом, область сходимости данного ряда состоит из одной точки 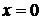 .
.
Пример 2. Найти область сходимости функционального ряда
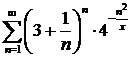 .
.
Решение. Из условия следует, что 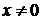 . Пусть
. Пусть 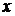 – фиксированное число, отличное от нуля. Исследуем сходимость получившегося числового ряда по радикальному признаку Коши:
– фиксированное число, отличное от нуля. Исследуем сходимость получившегося числового ряда по радикальному признаку Коши:
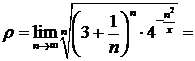
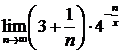
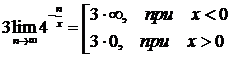 .
.
Итак, 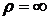 при
при 
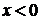 и ряд расходится,
и ряд расходится, 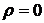 при
при 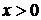 и ряд сходится. Поэтому область сходимости ряда
и ряд сходится. Поэтому область сходимости ряда 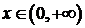 .
.
Пример 3. Исследовать на равномерную сходимость ряд 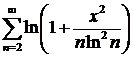 на
на 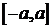 .
.
Решение. На 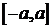 справедливо
справедливо
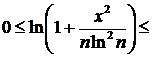
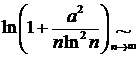
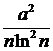 при
при 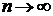 , а
, а 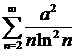 сходится (по интегральному признаку). Тогда
сходится (по интегральному признаку). Тогда 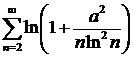 сходится (по теореме сравнения). Значит, по признаку Вейерштрасса данный ряд сходится равномерно на
сходится (по теореме сравнения). Значит, по признаку Вейерштрасса данный ряд сходится равномерно на 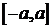 .
.
Пример 4. Исследовать на равномерную сходимость ряд
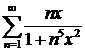 для
для 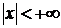 .
.
Решение. 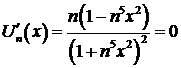 при
при 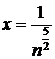 . Значит,
. Значит, 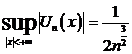 , но
, но 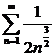 сходится. Тогда по признаку Вейерштрасса данный ряд сходится равномерно на всей числовой оси и абсолютно.
сходится. Тогда по признаку Вейерштрасса данный ряд сходится равномерно на всей числовой оси и абсолютно.
Задания для самостоятельной работы
n10.10. Найти область сходимости функционального ряда:
а) 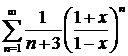 ; ; | б) 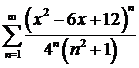 ; ; |
в) 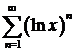 ; ; | г) 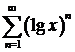 ; ; |
д) 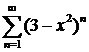 ; ; | е) 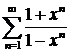 ; ; |
ж) 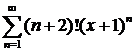 ; ; | з) 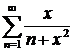 . . |
Ответы
10.10. а) 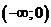 ; б)
; б) 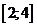 ; в)
; в) 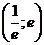 ; г)
; г) 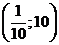 ; д)
; д) 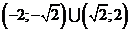 ; ж)
; ж) 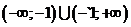 .
.
Степенные ряды
Примеры решения типовых задач
Пример 1. Найти область сходимости степенного ряда 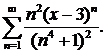
Решение. Интервал сходимости можно найти, применяя признак Даламбера или Коши к ряду, составленному из абсолютных величин членов исходного ряда. Здесь 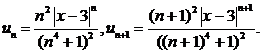
Вычислим предел
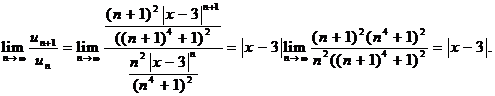
По признаку Даламбера для сходимости ряда предел должен быть меньше 1.
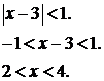
Исследуем сходимость ряда на концах промежутка 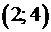 .
.
Если x = 4, то получим ряд 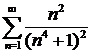 . Он сходится, так как этот ряд ведет себя как ряд
. Он сходится, так как этот ряд ведет себя как ряд 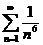 .
.
Если x = 2, то получим ряд 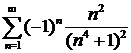 . Он сходится и притом абсолютно, так как сходится ряд из абсолютных величин его членов.
. Он сходится и притом абсолютно, так как сходится ряд из абсолютных величин его членов.
Окончательно получим, что область сходимости исследуемого ряда отрезок [2; 4].
Пример 2. Найти область сходимости функционального ряда
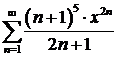 .
.
Решение. Данный ряд является степеннным. Он содержит только четные степени 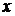 , поэтому искать радиус интервала сходимости по соответствующей формуле нельзя. Зафиксируем
, поэтому искать радиус интервала сходимости по соответствующей формуле нельзя. Зафиксируем 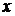 и исследуем сходимость получившегося числового ряда по признаку Даламбера.
и исследуем сходимость получившегося числового ряда по признаку Даламбера.
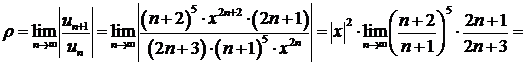
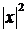 .
.
Ряд сходится, если 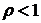 , т.е.
, т.е. 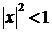 , откуда
, откуда 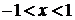 .
.
Исследуем поведение ряда на концах интервала сходимости.
При 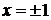 функциональный ряд принимает вид
функциональный ряд принимает вид
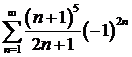 =
= 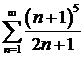 .
.
Этот числовой ряд расходится, так как не выполняется необходимый признак сходимости: 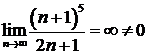 . Поэтому область сходимости данного ряда
. Поэтому область сходимости данного ряда 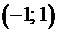 .
.
Пример 3. Найти сумму ряда 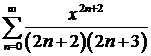 .
.
Решение. Представим коэффициент перед переменной в виде суммы простейших дробей 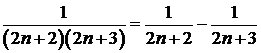 . Теперь данный ряд можно представить в виде алгебраической суммы двух рядов:
. Теперь данный ряд можно представить в виде алгебраической суммы двух рядов:
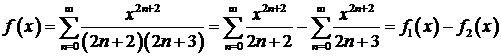 . Степенные ряды почленно интегрируются, поэтому
. Степенные ряды почленно интегрируются, поэтому 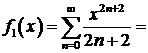
= 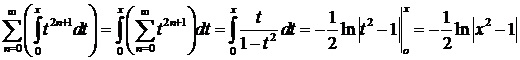 ,
,
при 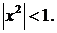 При замене ряда функцией воспользовались известной формулой – суммы бесконечно убывающей прогрессии
При замене ряда функцией воспользовались известной формулой – суммы бесконечно убывающей прогрессии 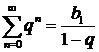 ,
, 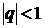 .
.
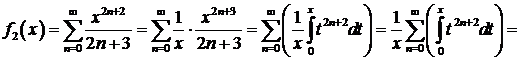
= 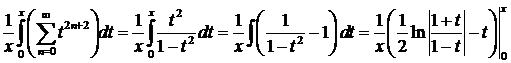 =
=
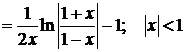 .
.
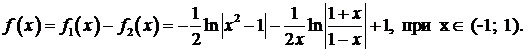
Пример 4. Найти сумму ряда 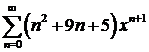 .
.
Решение. Представим коэффициент перед переменной в следующем виде 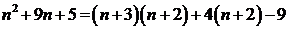 . Тогда данная сумма распадается на три:
. Тогда данная сумма распадается на три:
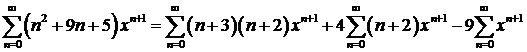
Степенные ряды можно почленно дифференцировать, поэтому
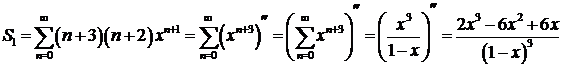 при
при 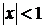 .
.
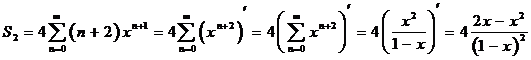
при 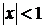 .
.
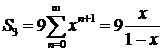 .
.
При замене суммы функцией воспользовались известной формулой суммы бесконечно убывающей геометрической прогрессии: 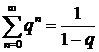 при
при 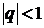 .
.
В итоге: 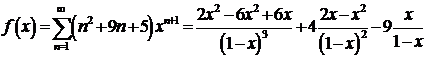
= 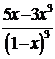 при n
при n 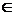 (-1; 1).
(-1; 1).
Задания для самостоятельной работы
10.11. Найти область сходимости степенного ряда:
а) 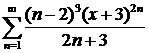 ; ; | б) 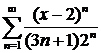 ; ; |
в) 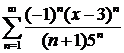 ; ; | г) 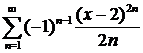 ; ; |
д) 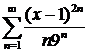 ; ; | е) 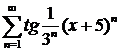 ; ; |
ж) 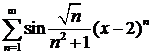 ; ; | з) 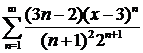 . . |
10.12. Найти сумму ряда:
а) 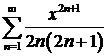 ; ; | б) 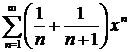 ; ; |
в) 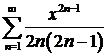 ; ; | г) 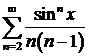 ; ; |
д) 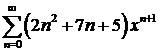 ; ; | е) 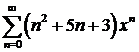 ; ; |
ж) 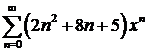 ; ; | з) 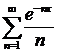 . . |
Ответы
10.11. а) 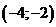 ; б)
; б) 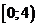 ; в)
; в) 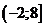 ; г)
; г) 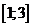 ; д)
; д) 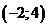 ; е)
; е) 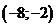 ; ж)
; ж) 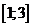 ; з)
; з) 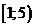 .
.
Разложение функций в ряды
Примеры решения типовых задач
Пример 1. Разложить функцию 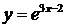 в степенной ряд по степеням (х – а) при а = 1. Определить область сходимости полученного ряда.
в степенной ряд по степеням (х – а) при а = 1. Определить область сходимости полученного ряда.
Решение. Ряд Тейлора для функции имеет вид:
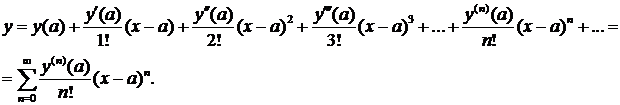 В нашем случае:
В нашем случае: 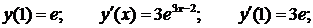
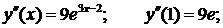
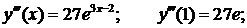
…………………………………..
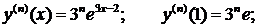
Получаем разложение в ряд:

Для определения области сходимости полученного ряда воспользуемся признаком Даламбера.
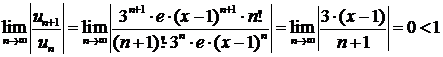 .
.
Следовательно, ряд сходится при любом конечном значении х.
Тот же факт можно доказать, если воспользоваться формулой для нахождения радиуса сходимости:
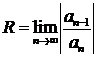 , где ап и ап-1 – коэффициенты ряда.
, где ап и ап-1 – коэффициенты ряда.
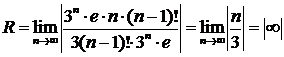 .
.
Полученный результат означает, что областью сходимости ряда является множество действительных чисел (-∞, +∞).
Пример 2. Разложить функцию 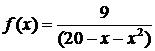 в ряд Тейлора по степеням х.
в ряд Тейлора по степеням х.
Решение. Разложим 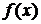 на элементарные дроби:
на элементарные дроби:
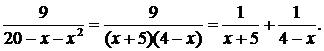
Воспользуемся готовой формулой: 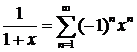 при
при 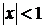 .
.
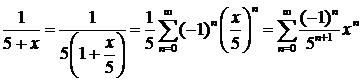 при
при 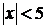 .
.
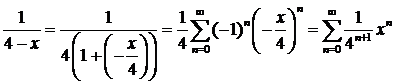 при
при 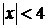 .
.
Сложив эти два выражения, окончательно получим:
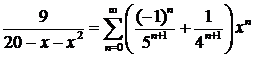 при
при 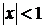 .
.
Пример 3. С точностью до е=0,001 вычислить интеграл 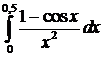 .
.
Решение. Так как интегрирование производится в окрестности точки х=0, то можно воспользоваться для разложения подынтегральной функцией рядом Маклорена (ряд Маклорена – это ряд Тейлора при а = 0).
Разложение функции 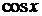 имеет вид:
имеет вид:
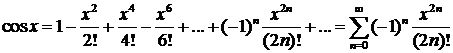 при
при 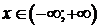 .
.
Зная разложение функции cosх, легко найти разложение функции
1–cosx:
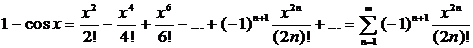 при
при 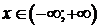 .
.
В этой формуле суммирование производится по п от 1 до бесконечности, а в предыдущей – от 0 до бесконечности. Это – не ошибка, так получается в результате преобразования.
Теперь представим в виде ряда подынтегральное выражение:
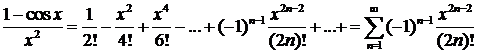
при 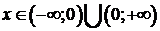 .
.
Тогда интеграл представим в виде:
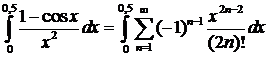 .
.
В предыдущем действии была применена теорема о почленном интегрировании ряда (т.е. интеграл от суммы был представлен в виде суммы интегралов от членов ряда). Для применения этой теоремы необходимо показать, что ряд сходится равномерно на отрезке интегрирования [0, 0,5]. Это требование выполняется, т.к. равномерная сходимость степенного ряда следует (по теореме Абеля) из сходимости ряда 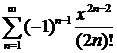 в точке
в точке 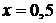 .
.
Радиус сходимости этого ряда равен:
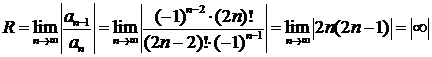 т.е. ряд сходится при любом конечном значении х.
т.е. ряд сходится при любом конечном значении х.
Итак,
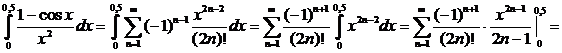
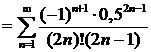 .
.
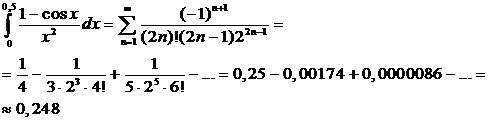
Видим, что абсолютные величины членов ряда очень быстро уменьшаются, и требуемая точность достигается уже при третьем члене разложения.
Для справки: точное (вернее – более точное) значение этого интеграла: 0,2482725418…
Пример 4. Найти 3 первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения:
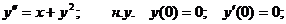
Решение. При данных начальных условиях решение уравнения будем искать в виде разложения в ряд Маклорена:
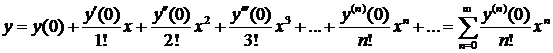 . Осталось только определить коэффициенты ряда. Первые два коэффициента уже известны из начальных условий. Для определения третьего коэффициента подставим начальные условия в дифференциальное уравнение:
. Осталось только определить коэффициенты ряда. Первые два коэффициента уже известны из начальных условий. Для определения третьего коэффициента подставим начальные условия в дифференциальное уравнение: 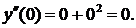
Таким образом, первые три члена разложения равны 0.
Для нахождения следующих членов разложения дифференцируем по х обе части дифференциального уравнения:
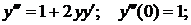
Первый ненулевой член разложения: 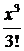 .
.
Для нахождения следующего члена разложения вновь дифференцируем только что полученное выражение по х. Находим значение в нуле и т.д. пока не получим еще два ненулевых члена разложения. При при наших начальных условиях придется дифференцировать 13 раз (!!!):
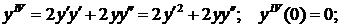
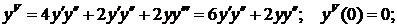
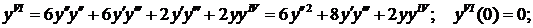
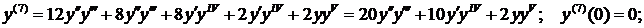
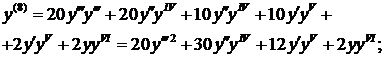
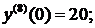
Нашли второй ненулевой член разложения: 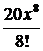 .
.
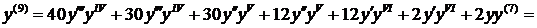
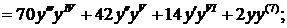
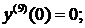
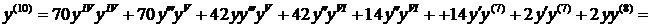
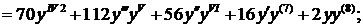
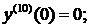
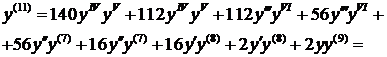
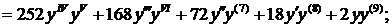
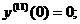
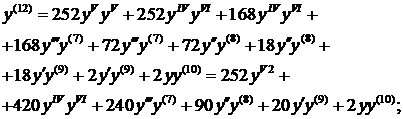
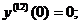
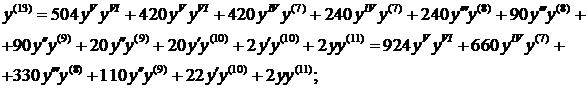
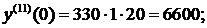
Теперь найден третий ненулевой член разложения: 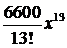 . Таким образом, решение дифференциального уравнения имеет вид:
. Таким образом, решение дифференциального уравнения имеет вид:
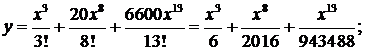
Подставим полученный результат в исходное уравнение:
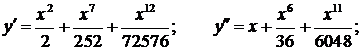
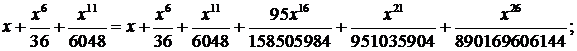
Видим, что при х достаточно близких к начальным условиям, последние три слагаемых практически равны нулю, и равенство выполняется.
Задания для самостоятельной работы
10.13. Разложить функцию в ряд Тейлора по степеням 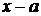 .
.
а) 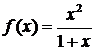 , , 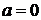 ; ; | б) 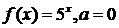 ; ; |
в) 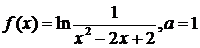 ; ; | г) 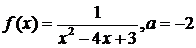 ; ; |
д) 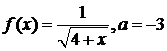 ; ; | е) 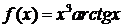 , , 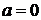 ; ; |
ж) 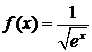 , , 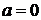 ; ; | з) 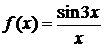 , , 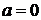 . . |
n10.14. Вычислить интеграл с точностью до 0,001.
а) 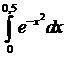 ; ; | б) 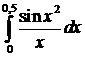 ; ; |
в) 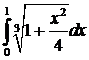 ; ; | г) 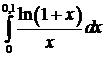 ; ; |
д) 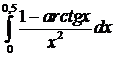 ; ; | е) 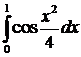 . . |
ж) 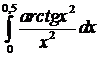 ; ; | з) 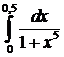 |
10.15. Вычислить указанную величину приближенно с заданной степенью точности 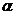 , воспользовавшись разложением в степенной ряд соответствующим образом подобранной функции:
, воспользовавшись разложением в степенной ряд соответствующим образом подобранной функции:
а) 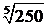 , , 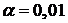 ; ; | б) 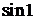 , , 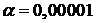 ; ; |
в) 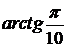 , , 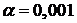 ; ; | г) 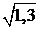 , ,
|
