Строим гистограмму распределения частот отказов по закону Вейбулла и полигон частот исходной выборки

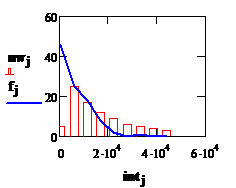
Вычисление критерия Хи-квадрат Пирсона распределения наработок до отказа по гипотезе закона Вейбулла:

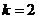
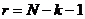Число степеней свободы

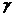Доверительная вероятность

Вычисляем квантиль Хи -квадрат распределения при заданной доверительной вероятности и числе степеней свободы

Вычисляем среднеквадратичное отклонение статистических и вычисленных значений частот отказов

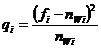
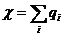
Сравнивая вычисленного значения критерия χ и значения квантили Х делаем вывод о верности гипотезы. Гипотеза экспоненциального закона распределения наработок до отказа может быть принята в случае если вычисленное значение меньше квантили.

Сделать выводы по работе:

1. Какими законами распределения, с какими параметрами, может быть представлена статистическая наработка.

2. Какими причинам отказов может быть описана рассмотренная статистическая наработка.

Контрольные вопросы

1. Как проверяется согласие эмпирического закона распределения случайной величины и выдвинутой гипотезы?

2. Что такое квантиль функции распределения случайной величины?

3. В каких случаях на практике встречается экспоненциальный закон распределения наработок до отказа?

4. Какие отказы чаще всего приводят к распределению наработок по закону Вейбулла?

5. Как по внешнему виду гистограммы можно обоснованно выдвинуть гипотезу о законе распределения случайной величины?

6. Как использовать коэффициент вариации для обоснования гипотезы о характере закона распределения случайной величины?

Лабораторная работа №3

«Определение закона надёжности невосстанавливаемых объектов

По малой случайно цензурированной выборке»

Теоретические основы

Существует большой класс технических объектов, статистическая информация о надежности которых по определению не может быть полной и достаточно определенной. Это, прежде всего, высоконадежные и малосерийные объекты, а также уникальные объекты, для которых нет прототипов (аналогов). Подразумевается, что объекты, для которых решается задача оценки надежности, созданы по единой технологии.

За длительный период наблюдения такие объекты могут иметь ограниченное количество отказов. Наработки неотказавших за этот же период объектов являются дополнительной (и весьма ценной) информацией о надежности всей контролируемой совокупности объектов. Эти наработки называют цензурирующими.

Цензурированием называется событие, приводящее к прекращению наблюдений за изделием до наступления системного события либо к свершению события в неизвестный момент времени в пределах некоторого интервала. Цензурированной выборкой называется выборка, элементами которой являются полные наработки и наработки до цензурирования (неполные наработки) или только значения наработки до цензурирования. Полной наработкой является наработка изделия от начала некоторого этапа его эксплуатации до системного события, например, наработка до отказа. Неполная наработка характеризует наработку изделия: от начала эксплуатации до фиксированного момента времени, но до наступления системного события; от некоторого произвольного момента, не связанного с системным событием, до системного события или до конкретного момента времени.

Интервал, в котором произошло или произойдет системное событие, причем точное значение наработки до системного события неизвестно, называется интервалом неопределенности. Этот интервал может быть ограниченным:

· слева (цензурирование слева). Наблюдения за объектами прекращаются в какой-то момент времени. К моменту окончания наблюдений часть объектов отказала. Другая часть продолжает работать, причем неизвестно, как долго эти объекты проработают без отказа;

· справа (цензурирование справа). К началу наблюдений объекты уже проработали некоторое неизвестное время без отказа. Отказавшие к моменту начала наблюдений объекты во внимание не принимаются;

· слева и справа (цензурирование интервалом). Цензурирование интервалом является наиболее общим случаем цензурирования.

Различают однократно и многократно цензурированные выборки. К однократно цензурированным относят, в частности, цензурированные слева выборки, содержащие полные и неполные наработки, причем все неполные наработки равны друг другу. Если у объектов наблюдения моменты или интервалы цензурирования различаются, то такие выборки являются многократно цензурированными. Применительно к задачам оценки надежности по результатам наблюдений в процессе эксплуатации цензурирование обычно связано с ограниченностью интервалов наблюдения.

Существует несколько типовых вариантов (планов) наблюдений. Краткое обозначение плана включает три элемента. Первый элемент характеризует количество объектов N, предназначенных для наблюдений. Второй – действия с отказавшими объектами: U – отсутствие замены или восстановления отказавших объектов; R – замена отказавших объектов; M – восстановление отказавших объектов. Третий элемент (одна или две буквы) определяет признак окончания наблюдений: T – наблюдения заканчиваются по истечении фиксированного интервала времени; r – наблюдения заканчиваются по достижении фиксированного количества реализаций (отказов, восстановлений); z – наблюдения заканчиваются при наработке каждого объекта, равной t_i.

План [NUT] указывает, что под наблюдением находится N объектов, отказавшие объекты не заменяются и не восстанавливаются U, наблюдения заканчиваются по истечении заданного интервала времени T (однократно цензурированная выборка). В отличие от [NUT] план [NUz] означает, что наблюдение за конкретным объектом заканчивается при возникновении его отказа или при достижении конкретного значения наработки (многократно цензурированная выборка). План [NUT] соответствует цензурированию типа 1, при этом заранее фиксируется время проведения наблюдений, число событий представляет собой случайную величину. При цензурировании по плану [NUr] или при цензурировании типа 2 заранее задается число событий (доля событий), после наступления которых наблюдения прекращаются, время наблюдения заранее не фиксируется, т.е. оно случайно.

Выбор конкретного плана зависит от целей исследования. Далее рассматриваются планы типа [… U …]. Обработка результатов по плану типа [… R …] сводится к предыдущему типу путем переноса начала наблюдений каждого нового объекта к некоторому условному началу испытаний всех объектов. Планы типа [… M …] можно рассматривать как планы типа [… U …], если каждую наработку между отказами трактовать как наработку некоторого невосстанавливаемого объекта (полное восстановление ресурса объекта после отказа). Очевидно, что план типа [NUN] соответствует полной выборке.

Оценка надежности проводится с начала эксплуатации на некоторый (текущий) момент или за определенный интервал времени. В первом случае имеет место цензурирование слева по текущему моменту времени. Для невосстанавливаемых объектов часть из них к этому моменту времени может отказать, а другая часть продолжает работать, что соответствует плану наблюдения [NUT]. Значения наработок исправных объектов неизвестны, но очевидно, что они превышают интервал наблюдения. Во втором случае оценка надежности связана с цензурированием выборки справа (продолжительность работы средств точно неизвестна) и слева, часть средств может отказать к моменту начала наблюдения и не учитывается на текущем интервале, другая часть может отказать на текущем интервале, а третья продолжит работу и по завершении периода наблюдения. В рассмотренных вариантах цензурирование осуществляется по фиксированным моментам времени, и число наблюдений в выборке является случайным.

В некоторых случаях цензурирование осуществляется по конкретным событиям, например, при определенном числе отказов объектов, что характерно при проведении испытаний однотипных изделий в интересах определения показателей надежности, планы типа [NUr]. В планах наблюдения [NU(r,T)] прекращение наблюдений происходит после отказа r объектов или по достижении момента времени Т в зависимости от того, какое из событий происходит ранее. В таких случаях объем выборки не является случайным, случайна продолжительность наблюдений.

Итак, формируемые в ходе эксплуатации выборки по надежности могут иметь: однократное цензурирование слева (например, период наблюдения от начала эксплуатации до текущего момента времени); цензурирование интервалом (период наблюдения определяется календарными сроками); многократное цензурирование слева; многократное цензурирование интервалом. Левая и правая границы цензурирования при этом определяются моментами времени или случайными событиями, например, моментом отказа какого-либо средства.

Для цензурированных выборок необходимо применять свои методы оценки показателей, проверки статистических гипотез. Теория обработки цензурированных выборок сложнее традиционных методов математической статистики и далека от своего завершения.

Следует отметить, что практически все выборки результатов наблюдения за функционированием объектов так или иначе цензурированы. Однако цензурирование следует учитывать только в тех случаях, когда интервал наблюдения соизмерим с наработкой на системное событие и количество неполных наблюдений составляет значительный процент в общем объеме.

Порядок выполнения работы

Исходная информация:

М - матрица случайноцензурированных выборок наработок объектов до отказов и до приостановки наблюдения;

- второй столбец матрицы - это индикаторный массив, единица ставится в случае, если соответствующая наработка является наработкой объекта до отказа, в противном случае в индикаторном массиве ставится нуль.

Используя матрицу выборок, строим статистическую функцию распределения

где N–количество объектов;

F_i-1– предыдущее значение функции распределения;

– значение индикаторного массива.

Сглаживание рассчитанной функции распределения пометоду скользящей медианы (функция medsmoth MathCAD)

и простейшим способом

Построить графики функций F,F1,F2.

Сделать выводы

1. Что такое восстановленная функция распределения наработки до отказа?

2. Вероятность того, что объект проработает время большее, чем ... чравна ....

3. Вероятность того, что объект откажет при наработке не более .... ч равна ....

4. Каким образом получить более полный анализ показателей надёжности?

Контрольные вопросы

1. Что такое цензурированная выборка наработок объекта?

2. Какие виды цензурирований встречаются на практике?

3. Как влияет цензурирование на показатели надёжности технических объектов?

4. Что такое функция надёжности?

5. Что такое функция ненадёжности?

6. Изобразить график плотности распределения наработок до отказа при нормальном законе надёжности?

Лабораторная работа №4

«Расчёт функции готовности и коэффициента готовности энергоблока»

Теоретические основы

При расчете показателей надежности восстанавливаемых объектов и систем наиболее распространено допущение:

• экспоненциальное распределение наработки между отказами;
• экспоненциальное распределение времени восстановления.

Допущение во многом справедливо, поскольку во-первых, экспоненциальное распределение наработки описывает функционирование системы на участке нормальной эксплуатации, во-вторых, экспоненциальное распределение описывает процесс без «предыстории».

Применение экспоненциального распределения для описания процесса восстановления позволяет при ординарных независимых отказах представить анализируемые системы в виде марковских систем.

При экспоненциальном распределении наработки между отказами и времени восстановления, для расчета надежности используют метод дифференциальных уравнений для вероятностей состояний (уравнений Колмогорова-Чепмена).

Случайный процесс в какой либо физической системе S, называется марковским, если он обладает следующим свойством: для любого момента t₀ вероятность состояния системы в будущем (t > t₀) зависит только от состояния в настоящем (t = t₀) и не зависит от того, когда и каким образом система пришла в это состояние (иначе: при фиксированном настоящем будущее не зависит от предыстории процесса - прошлого).

t < t0

t > t0

Для марковского процесса «будущее» зависит от «прошлого» только через «настоящее», т. е. будущее протекание процесса зависит только от тех прошедших событий, которые повлияли на состояние процесса в настоящий момент.

Марковский процесс, как процесс без последействия, не означает полной независимости от прошлого, поскольку оно проявляется в настоящем.

При использовании метода, в общем случае, для системы S, необходимо иметь математическую модель в виде множества состояний системы S₁ , S₂ , … , S_n , в которых она может находиться при отказах и восстановлениях элементов.

Для рассмотрения принципа составления модели введены допущения:

- отказавшие элементы системы (или сам рассматриваемый объект) немедленно восстанавливаются (начало восстановления совпадает с моментом отказа);

- отсутствуют ограничения на число восстановлений;

- если все потоки событий, переводящих систему (объект) из состояния в состояние, являются пуассоновскими (простейшими), то случайный процесс переходов будет марковским процессом с непрерывным временем и дискретными состояниями S₁ , S₂ , … , S_n .

Основные правила составления модели:

1. Математическую модель изображают в виде графа состояний.

Элементы графа:

а) кружки (вершины графа S₁ , S₂ , … , S_n ) – возможные состояния системы S, возникающие при отказах элементов;

б) стрелки – возможные направления переходов из одного состояния S_i в другое S_j .

Над/под стрелками указываются интенсивности переходов.

Примеры графа:

S0 – работоспособное состояние;

S1 – состояние отказа.

«Петлей» обозначаются задержки в том или ином состоянии S0 и S1 соответствующие:

- исправное состояние продолжается;

- состояние отказа продолжается (в дальнейшем петли на графах не рассматриваем).

Граф состояний отражает конечное (дискретное) число возможных состояний системы S₁ , S₂ , … , S_n . Каждая из вершин графа соответствует одному из состояний.

2. Для описания случайного процесса перехода состояний (отказ/ восстановление) применяют вероятности состояний

P1(t), P2(t), … , P_i(t), … , Pn(t),

где P_i(t) – вероятность нахождения системы в момент t в i-м состоянии, т. е.

P_i(t) = P{S(t) = Si}.

Очевидно, что для любого t

(нормировочное условие, поскольку иных состояний, кроме S₁ , S₂ , … , S_n нет).

3. По графу состояний составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова-Чепмена), имеющих вид:

В общем случае, интенсивности потоков _ij и _ij могут зависеть от времени t.

При составлении дифференциальных уравнений пользуются простым мнемоническим правилом:

а) в левой части – производная по времени t от P_i(t);

б) число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;

в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;

г) знак произведения положителен, если стрелка входит (направлена острием) в рассматриваемое состояние, и отрицателен, если стрелка выходит из него.

Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений.

4. Чтобы решить систему дифференциальных уравнений для вероятностей состояний P1(t), P_i(t), … , Pn(t) необходимо задать начальное значение вероятностей

P1(0), P_i(0), … , Pn(0), при t = 0,

сумма которых равна единице:

Если в начальный момент t = 0 состояние системы известно, например, S(t=0) = Si, то P_i(0) = 1, а остальные равны нулю.

В качестве примера вычисления показателей надежности, рассмотрен восстанавливаемый объект, у которого поток отказов простейший (пуассоновский) с параметром потока

= = 1/ T₀,

а распределение времени восстановления подчиняется экспоненциальному распределению с интенсивностью восстановления

= 1/ T_В ,

где T0 – средняя наработка между отказами;

T_В – среднее время восстановления.

P₀(t) – вероятность работоспособного состояния при t;

P₁(t) – вероятность неработоспособного состояния при t.

Система дифференциальных уравнений:

Начальные условия: при t = 0 P₀(t = 0) = P₀(0) = 1; P₁(0) = 0, поскольку состояния S₀ и S₁ представляют полную группу событий, то

P₀(t) + P₁(t) = 1.

Выражая P₀(t) = 1 - P₁(t), получаем одно дифференциальное уравнение относительно P₁(t):

dP₁(t)/dt = (1 – P₁(t)) - P₁(t).

Решив уравнение определим вероятность нахождения объекта в неработоспособном состоянии:

Тогда вероятность нахождения в работоспособном состоянии P0(t) = 1 - P1(t), равна

С помощью полученных выражений можно рассчитать вероятность работоспособного состояния и отказа восстанавливаемого объекта в любой момент t.