Третий этап — книгопечатание

Книгопечатание можно смело назвать первой информационной технологией. Воспроизведение информации было поставлено на поток, на промышленную основу. По сравнению с предыдущим этот этап не столько увеличил возможности по хранению (хотя и здесь был выигрыш: письменный источник — часто один-единственный экземпляр, печатная книга — целый тираж экземпляров, а, следовательно, и малая вероятность потери информации при хранении (вспомним «Слово о полку Игореве»)), сколько повысил доступность информации и точность её воспроизведения.

Четвёртый (последний) этап предыстории

связан с успехами точных наук (прежде всего математики и физики) и начинающейся в то время научно-технической революцией. Этот этап характеризуется возникновением таких мощных средств связи, как радио, телефон и телеграф, к которым по завершению этапа добавилось и телевидение.

Кроме средств связи появились новые возможности по получению и хранению информации — фотография и кино. К ним также очень важно добавить разработку методов записи информации на магнитные носители (магнитные ленты, диски).

Информация перерабатывается не машинными, а рутинными способами!

Начало истории информатики

Связано с разработкой первых ЭВМ. Во-первых, сам термин «информатика» появился на свет благодаря развитию вычислительной техники, и поэтому под ним понималась наука о вычислениях (первые ЭВМ большей частью использовались для проведения числовых расчётов). Во-вторых, выделению информатики в отдельную науку способствовало такое важное свойство вычислительной техники, как единая форма представления обрабатываемой и хранимой информации. Вся информация хранится и обрабатывается на ЭВМ в двоичной форме. Компьютер объединил хранение и обработку числовой, текстовой (символьной) и аудиовизуальной (звук, изображение) информации.

Информатика: ИТ и АИС

В современных понятиях информатика связывается с информационными технологиями (ИТ), и реализующими их автоматизированными информационными системами (АИС).

Информационные технологии

Информационная технология – процесс, использующий совокупность средств и методов сбора, обработки и передачи данных (первичной информации) для получения информации нового качества о состоянии объекта, процесса или явления (информационного продукта).

ИТ включают два основных элемента — машинный и человеческий (социальный) – который выступает главным элементом.

Автоматизированные информационные системы

Автоматизированная информационная система (АИС) представляет собой совокупность информации, экономико-математических методов и моделей, технических, программных, технологических средств и специалистов, предназначенная для обработки информации и принятия управленческих решений.

Структура АИС как совокупность 6-ти обеспечивающих подсистем

технического обеспечения

математического обеспечения

программного обеспечения

информационного телекоммуникационного обеспечения

организационного обеспечения

правового обеспечения

Основные этапы технологического процесса в АИС

Событие->Сбор->Возможное преобразование информации->Передача ->Обработка на ЭВМ ->Хранение ->Передача ->Воспроизведение информации ->Потребитель информации

Классификация АИС

В настоящее время АИС получили широчайшее распространение. Классификация АИС осуществляется по ряду признаков, и в зависимости от решаемой задачи можно выбрать разные признаки классификации. При этом одна и та же АИС может характеризоваться одним или несколькими признаками. В качестве признаков классификации АИС используются:

область применения,

охватываемая территория (от ОГАИС до АИС город),

организация информационных процессов,

направление деятельности,

назначения, структура и др.

Значение информационных технологий

Говорить о воздействии науки на что-либо вне информационного процесса бессмысленно. Научная идея должна превратиться в информацию, т.е. быть закодированной, переданной по каналу связи, принятой адресатом, чтобы её можно было применить на практике. Знания должны определённым образом фиксироваться, трансформироваться, распределяться, приниматься и перерабатываться.

Информационные технологии и выступают новым средством превращения знаний в информационный ресурс (ИР) общества. ИТ стали также средством эффективного использования ИР.

Информационный ресурс общества

Информационные ресурсы – это знания, подготовленные людьми для социального использования в обществе и зафиксированные на материальном носителе. Информационные ресурсы общества (знания) отчуждены от тех людей, которые их создавали, накапливали, анализировали и т.д.

Эти знания материализовались в виде: документов, баз данных, баз знаний, алгоритмов, компьютерных программ, произведений искусства, литературы, науки.

Информационный ресурс страны, общества рассматривается как стратегический ресурс, аналогичный по значимости сырьевому и энергетическим ресурсам.

Предметная область информатики

Информационный ресурс стал основным ресурсом человечества, главной ценностью современной цивилизации.

Таким образом, предметом информатики является информационный ресурс как симбиоз знания и информации

Итак, «оттолкнувшись от ЭВМ», информатика во главу угла ставит новые понятия — ИР и его социальную полезность, отдачу. Поэтому по аналогии с термодинамикой информатику можно назвать информдинамикой — наукой о развитии социальных систем под воздействием ИР (семантической информации).

Раздел 2 (Лекции 2-3)

Термин Информация

Термин информацияимеет множество определений. В «Энциклопедии кибернетики» читаем: «информация ( лат. informatio — разъяснение, изложение, осведомленность ) — одно из наиболее общих понятий науки, обозначающее некоторые сведения, совокупность каких-либо данных, знаний».

«Информация» в широком смысле—отражение реального мира; в узком смысле «информация» — это любые сведения, являющиеся объектом хранения, передачи и преобразования.

Информация – это сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают имеющуюся о них степень неопределенности, неполноты знаний.

С практической точки зрения информация всегда представляется в виде сообщения.

Термин данные

Очень широко используется еще один термин: данные(лат. data). Этот термин применяется к информации, представленной в виде, позволяющем хранить, передавать или обрабатывать ее с помощью технических средств.

Поэтому наряду с терминами ввод информации, обработка информации, хранение информации, поиск информации используются термины ввод данных, обработка данных, хранение данных и т. п.

Общая схема передачи информации

Источник сообщений -> Кодирующее устройство -> Канал связи -> Декодирующее устройство -> Получатель сообщений

Информационное сообщение

Сообщение от источника к получателю (приемнику) передается в материально-энергетической форме (электрический, световой, звуковой сигналы и т. д.). Человек воспринимает сообщения посредством органов чувств.

Приемники информации в технике воспринимают сообщения с помощью различной измерительной и регистрирующей аппаратуры.

В обоих случаях с приемом информации связано изменение во времени какой-либо величины, характеризующей состояние приемника.

Информационное сообщение представим функцией х(t)

Функция х(t), характеризует изменение во времени материально-энергетических параметров физической среды, в которой осуществляются информационные процессы.

Функция х(t) принимает любые вещественные значения в диапазоне изменения времени (t).

Аналоговая и дискретная информация

Если функция х(t) непрерывна, то имеет место непрерывная или аналоговая информация, источником которой обычно являются различные природные объекты (например, температура, давление и влажность воздуха), объекты технологических производственных процессов (например, нейтронный поток в активной зоне, давление и температура теплоносителя в контурах ядерного реактора) и др.

Если функция х(t) дискретна, то информационные сообщения, используемые человеком, имеют характер дискретных сообщений (например, сигналы тревоги, передаваемые посредством световых и звуковых сообщений, языковые сообщения, передаваемые в письменном виде или с помощью звуковых сигналов; сообщения, передаваемые с помощью жестов, и др.).

Термин Вычислительная машина (Компьютер)

В современном мире информация обрабатывается на вычислительных машинах. Поэтому информатика тесно связана с инструментарием — вычислительной машиной (ВМ).

Computer— устройство преобразования информации посредством выполнения управляемой программой последовательности операций.

Синоним компьютера — вычислительная машина, чаще электронная вычислительная машина (ЭВМ).

Классификация вычислительных машин

АВМ и ЦВМ

Аналоговая вычислительная машина (АВМ) — это машина, оперирующая информацией, представленной в виде непрерывных изменений некоторых физических величин.

При этом в качестве физических переменных используются сила тока электрической цепи, угол поворота вала, скорость и ускорение движения тела и т. п.

Используя тот факт, что многие явления в природе математически описываются одними и теми же уравнениями, АВМ позволяют с помощью одного физического процесса моделировать различные процессы.

Цифровая вычислительная машина (ЦВМ) — машина, оперирующая информацией, представленной в дискретном виде.

В настоящее время разработаны методы численного решения многих видов уравнений, что дало возможность решать на ЦВМ различные уравнения и задачи с помощью набора простых арифметических и логических операций.

Поэтому, если АВМ обычно предназначаются для решения определенного класса задач, т.е. являются специализированными, то ЦВМ, как правило, являются универсальным вычислительным средством.

Алфавитный способ Представление дискретной информации в ЭВМ

Алфавитный способ основан на использовании фиксированного конечного набора символов любой природы, называемого алфавитом.

Примерами алфавитов могут служить алфавиты естественных человеческих языков, совокупность десятичных цифр, любая другая упорядоченность знаков, предназначенная для образования и передачи сообщений.

Символы из набора алфавита называются буквами, а любая конечная последовательность букв — словомв этом алфавите. При этом не требуется, чтобы слово обязательно имело языковое смысловое значение.

Процессы кодирования и декодирования информации

Все процессы, происходящие в вычислительной системе, связаны непосредственно с различными физическими носителями информационных сообщений, а все узлы и блоки этой системы являются физической сферой, в которой осуществляются информационные процессы.

Процесс преобразования информации часто требует представлять буквы одного алфавита средствами (буквами, словами) другого алфавита. Такое представление называется кодированием.

Процесс обратного преобразования информации относительно ранее выполненного кодирования называется декодированием.

Классификация информации

Рассмотрим следующий перечень: генетическая информация; геологическая информация; синоптическая информация; ложная информация (дезинформация); полная информация; экономическая информация; техническая информация и т. д.

Действительно, что в этом перечне приведены не все виды информации, кроме того, от этого перечня мало проку.

Этот перечень не систематизирован. Для того чтобы классификация по видам была полезной, она должна быть основана на некоторой системе. Обычно в качестве базы для классификации используется то или иное свойство (может быть наборсвойств) объектов.

Свойства информации: внутренние и внешние

Как правило, свойства объектов можно разделить на два больших
класса: внешние и внутренние свойства.

Внешние свойства — это свойства, характеризующие поведение объекта при взаимодействии с другими объектами.

Внутренние свойства — это свойства, органически присущие объекту. Они обычно «скрыты» от изучающего объект и проявляют себя косвенным образом при взаимодействии данного объекта с другими.

Качество информации

Качество информации — обобщённая положительная характеристика информации, отражающая степень её полезности для потребителя.

Показатель качества— одно из важных положительных свойств информации (с позиции потребителя).

Чаще всего рассматривают показатели качества, которые можно выразить числом, и такие показатели являются количественными характеристиками положительных свойств информации.

При этом, любое отрицательное свойство
может быть заменено обратным ему, положительным

Показатели качества

Релевантность— способность информации соответствовать нуждам (запросам) потребителя.

Полнота— свойство информации исчерпывающе (для данного потребителя) характеризовать отображаемый объект или процесс.

Своевременность— способность информации соответствовать нуждам потребителя в нужный момент времени.

Достоверность— свойство информации не иметь скрытых ошибок.

Набор важнейших показателей качества информации

Релевантность— способность информации соответствовать нуждам (запросам) потребителя.

Полнота— свойство информации исчерпывающе (для данного потребителя) характеризовать отображаемый объект или процесс.

Своевременность— способность информации соответствовать нуждам потребителя в нужный момент времени.

Достоверность— свойство информации не иметь скрытых ошибок.

Доступность— свойство информации, характеризующее возможность ее получения данным потребителем.

Защищённость— свойство, характеризующее невозможность несанкционированного использования или изменения информации.

Эргономичность— свойство, характеризующее удобство формы или объема информации с точки зрения данного потребителя.

Конфиденциальность – свойство информации быть известной только допущенным и прошедшим проверку (авторизацию) субъектам (пользователям, процессам, программам)

Адекватность информации

Адекватность – это свойство информации однозначно соответствоватьотображаемому объекту или явлению.

Это вторая группа внешних свойств информации с точки зрения: информация – отображаемый объект.

Адекватность также является для потребителя внутренним свойством информации, проявляющим себя через релевантность и достоверность

Внутренние свойства информации

Среди внутренних свойств информации важнейшими являются два:

объем (количество) информации и её внутренняя организация – структура.

Об объёме и количестве информации речь пойдёт позднее, а по способу ее внутренней организации информацию делят на две группы:

1. Данные или простой, логически неупорядоченный набор сведений.

2. Логически упорядоченные, организованные наборы данных.

Упорядоченность достигается наложением на данные некоторой структуры (отсюда часто используемый термин — структура данных).

Знания и их свойства

Во второй группе выделяют особым образом организованную информацию — знания.

Знания (в отличие от данных) представляют информацию не о каком-то единичном и конкретном факте, а о том, как устроены все факты определённого типа.

Знания обладают свойствами:

Внутренняя интерпретируемость

Структурированность

Связанность

Активность
Все эти свойства знаний в конечном итоге обеспечивают возможность моделировать рассуждения человека в системах искусственного интеллекта.

Методы и модели оценки количества информации

Как и для характеристик вещества (вспомним массу, заряд, объем и т.д.), так и для характеристик информации имеются единицы измерения, что позволяет некоторой порции информации приписывать числа — количественные характеристики информации.

Способы измерения информации

На сегодняшний день наиболее известны следующие способы измерения информации:

Объёмный (самый простой и грубый),

Энтропийный (принят в теории информации и кодировании),

Алгоритмический (оценка сложности и размера соответствующей программы).

Объёмный способ измерения информации

Объем информации в сообщении — это количество символов в сообщении.

Поскольку, например, одно и то же число может быть записано многими разными способами (с использованием разных алфавитов), то этот способ чувствителен к форме представления (записи) сообщения.

Единицы измерения объёма

В вычислительной технике вся обрабатываемая и хранимая информация представлена в двоичной форме (с использованием алфавита, состоящего всего из двух символов 0 и 1).

Такая стандартизация позволила ввести две стандартные единицы измерения: бит и байт.

Бит— количество информации, которое может помещаться в один элемент памяти.

Байт — это восемь бит.

Энтропийный способ измерения количества информации

Этот способ измерения исходит из следующей модели. Получатель информации (сообщения) имеет определённые представления о возможных наступлениях некоторых событий. Эти представления в общем случае недостоверны и выражаются вероятностями P_i, с которыми он ожидает то или иное событие.

Общая мера неопределённости (энтропия) характеризуется некоторой математической зависимостью от совокупности этих вероятностей.

Количество информации в сообщении определяется тем, насколько уменьшится эта мера неопределённости после получения сообщения.

Формула Шеннона

Количество информации в сообщении, состоящем из N символов
H= - SP_ilog₂ P_i, где i изменяется от 1 до N,

P_i - это вероятность i-ого символа.

P_i= 1/Nпри равновероятных символах.

H=log₂N, где N - число возможных равновероятных символов в сообщении.

Формула Хартли

Используется для оценки количества информации H в сообщении, передаваемого по каналу связи числовым кодом.

Пусть m – основание системы счисления (число букв алфавита)

Пусть n – число разрядов в сообщении.

Тогда N = mⁿ - число всевозможных кодовых комбинаций сообщения.

При равновероятном появлении любой кодовой комбинации количество информации, приобретённое получателем:

H=log₂ N = log₂ mⁿ = n log₂ m

Информативность сообщения

При условии полного априорного незнания получателем сообщения, передаваемого по каналу связи двоичным кодом, количество информации равно количеству символов в сообщении (числу разрядов), т.е. объёмный (V) и энтропийный (H) способ измерения дают один и тот же результат: H=V=n, бит

При наличии некоторой априорной информации, т.е. при не равновероятных символах в сообщении, всегда H<V=n.

K_инф = H/V, [0, 1] Для увеличения K_инф разрабатываются методы оптимального кодирования информации.

Алгоритмический способ измерения информации

Этот метод кратко можно охарактеризовать следующими рассуждениями.

Каждый согласится, что слово 0101…01 сложнее слова 00...0, а слово, где 0 и 1 выбираются из эксперимента — бросания монеты (где 0 — герб, 1 — решка), сложнее обоих предыдущих.

Понятие Машины Тьюринга

Так как имеется много разных вычислительных машин и разных языков программирования (разных способов задания алгоритма), то для определенности задаются некоторой конкретной вычислительной машиной, например, абстрактной машиной Тьюринга.

А предполагаемая количественная характеристика — сложность слова (сообщения) определяется как минимальное число внутренних состояний машины Тьюринга, требующиеся для его воспроизведения.

Основные понятия теории алгоритмов

В информатике алгоритмы рассматриваются в двух аспектах: теоретическом и прагматическом, тесно связанным с программированием.

Теория алгоритмов — раздел математики, изучающий общие свойства алгоритмов.

Понятие «алгоритм» сформировалось в математике в 20-х годах XX в. Началом систематической разработки теории алгоритмов можно считать 1936 г. и связывают это начало с публикацией работы А.А. Черча.

Алгоритмическая модель и её составляющие

Составляющими такой модели должны быть конкретный набор элементарных шагов, способы определения следующего шага. Каждый шаг должен быть элементарным и выполнимым, чтобы алгоритм понимался однозначно.

От модели также требуется простота и универсальность. Универсальность необходима для того, чтобы модель позволяла описать любой алгоритм.

Требование простоты важно для того, чтобы выделить необходимые элементы и свойства алгоритма и облегчить доказательства общих утверждений об этих свойствах.

Три основных класса алгоритмических моделей

Первый класс моделей основан на арифметизации алгоритмов.

Второй класс моделей основан на идее машинизации алгоритмов: он должен быть представлен так, чтобы его могла выполнять вычислительная машина.

Третий класс моделей алгоритмов оперирует конкретными алфавитами, здесь наиболее известная алгоритмическая модель— нормальные алгоритмы Маркова.

Первый. Предполагается, что любые данные можно закодировать числами, и как следствие — всякое их преобразование становится в этом случае арифметическим вычислением, алгоритмом в таких моделях является вычисление значения некоторой числовой функции, а его элементарные шаги — арифметические операции.

Последовательность шагов определяется двумя способами. Первый способ — суперпозиция, т.е. подстановка функции в функцию, а второй — рекурсия, т.е. определение значения функции через «ранее» вычисленные значения этой же функции. Функции, которые можно построить из целых чисел и арифметических операций с помощью суперпозиций и рекурсивных определений, называются рекурсивными функциями. Например: n! (n+1)

Второй. Основные составные части машины Тьюринга: (УУ) — управляющееустройство, 1 — лента, 2 - головка;
А = {а₁... а_m}— алфавитмашины; Q= {q₁… q_n} — множество состояний машины (точнее, головки), среди которых выделяют начальное q₁и конечное q_z

Третий. Для нормального алгоритма задается алфавит, над которым он работает, конечное множество допустимых подстановок и правила их применения:

1) проверить возможность подстановок в порядке возрастания их номеров, и если она возможна (левая часть подстановки обнаружена в исходном слове), произвести подстановку (заменив левую часть на правую);

2) если в примененной подстановке имеется символ «!», то
преобразования прекращаются, а если нет, то текущее состояние становится исходным и весь процесс начинается заново;

3) если ни одна подстановка не применима, то процесс преобразования завершен.

Описание машины Тьюринга

Машина Тьюринга состоит из трех частей: ленты, головки и управляющего устройства. Лента бесконечна в обе стороны и разбита на ячейки. В каждой ячейке может быть записан только один символ. Отсутствие символа в ячейке обозначается специальным «пустым» символом, например, « ».

Головка всегда располагается над некоторой ячейкой ленты. Она может читать и писать символы, стирать их и перемещаться вдоль ленты как вправо так и влево.

Пример машинной модели (алгоритм сложения)

Пусть m и n неотрицательные целые числа произвольной длины.

Числа представляются счётно-импульсным кодом, т.е. количеством 1, равныхmили, соответственно,n.

Необходимо построить алгоритм вычисления m+n.

Зададим алфавит машины Тьюринга:

А = { #,1,0 } , где

# - отсутствие символа в ячейке ленты

1 - символ кода числа

0 – символ разделения двух чисел

Начальная конфигурация q₁ a₁

Конечная конфигурация a₂ q_k

Покажем, что число 4 характеризует сложность алгоритма сложения и не зависит от длины входных данных. Для этого запишем набор команд машины Тьюринга и найдем необходимое число внутренних состояний машины.

Команды машины: q_ia_k>q_ja_ld_p

q₁# >q₁# RR – Right

q₁1 > q₁1 R

q₁0 > q₂1 R

q₂1 > q₂1 R

q₂# > q₃# L L – Left

q₃1 > q₄# S S- Stop

АлгоритмыМаркова

зададим алгоритм преобразования исходного слова «СЛОН»
в слово «МУХА» по следующей цепочке:

«СЛОН» —» «СУОН» —>«МУОН» —>«МУХН» —» «МУХА».
Используя множество подстановок

1. Я-У2. Л-У3. С - М 4. В- Б 5. Р-Т6. Т-Р! 7. О-Х8. Н -А

Понятие алгоритмически неразрешимой задачи

Появление точного понятия алгоритма позволило сформулировать алгоритмически не разрешимые проблемы, т.е. задачи, для решения которых невозможно построить алгоритм. Задача называется алгоритмически неразрешимой, если не существует машины Тьюринга (или рекурсивной функции, или нормального алгоритма Маркова), которая её решает. Например, неразрешимой оказалась проблема распознавания эквивалентности алгоритмов: нельзя построить алгоритм, который по любым двум алгоритмам (программам) выяснял бы, вычисляют они одну и ту же функцию или нет. Знание основных неразрешимостей теории алгоритмов необходимо для специалиста по информатике. Оно предостережёт его от увлечения глобальными прожектами всеобщей алгоритмизации точно так же, как знание основных законов физики предостерегает от попыток создания вечного двигателя.

Раздел 3 (Лекции 4-5)

Системы счисления

В вопросах организации обработки информации на ЦВМ важное место занимают системы счисления, формы представления данных, специальное кодирование чисел.

Системой счисления называется совокупность приемов наименования и записи чисел.

Системы счисления различаются выбором алфавита, базисных чисел и правилами образования из них остальных чисел.

Алфавит систем счисления

Напомним, что алфавитом называется фиксированный конечный (упорядоченный) набор символов любой природы.

В современных системах счисления используется алфавит, включающий как арабские цифры 0, 1, 2, …9., так и буквы латинского алфавита, например, I, V, X, L, C, D, M и т.д.

Базисные числа систем счисления

В любой системе счисления каждому символу из набора алфавита – букве - приписывается базисное число. Например, в римской системе используются буквы I, V, X, L, С, D, М, которым соответствуют базисные числа 1, 5, 10, 50, 100, 500, 1000.

В 16-чной системе счисления используется алфавит, состоящий из 9 арабских цифр и 6 латинских букв: 0, 1, 2, 3, …9, A, B, C, D, E, F. Базисные числа 0, 1, 2, 3, …9, 10, 11, 12,…15.

Аддитивно-мультипликативные системы счисления

Системы счисления, в которых любое число получается путем умножения и сложения базисных чисел, называются аддитивно-мультипликативными.

Все известные позиционные системы счисления являются аддитивно-мультипликативными. Особенно отчетливо аддитивно-мультипликативный способ образования чисел из базисных выражен в числительных русского языка, например пятьсот шестьдесят восемь (т.е. пять сотен плюс шесть десятков плюс восемь).

Позиционные системы счисления

Для изображения (или представления) чисел в настоящее время используются в основном позиционные системы счисления.

Система называется позиционной, если числовое значение каждой буквы алфавита зависит не только от приписанного ей базисного числа, но и от ее положения (позиции) в слове, изображающем число.

Основание позиционной системы счисления

ЧислоКединиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления, а сама система счисления называется К-ичной.

Например, основанием десятичной СС является числоК=10, троичной – число К=3, двоичной – число К=2, шестнадцатеричной – число К=16. В Древнем Вавилоне широко использовалась система счисления с основаниемК=60.

Запись и изображение произвольного числа Xв К-ичной позиционной системе счисления

Запись произвольного числа X в К-ичной позиционной системе счисления основывается на представлении этого числа в виде полинома:

где каждый коэффициент а_iможет быть одной из букв алфавита данной СС и изображается одним знаком.

Число X, представленное в К-ичной системе счисления, можно кратко записать писать в виде

а_nа_n-1...а₁а₀.а_-1...а_-т...

т.е. путем перечисления всех коэффициентов полинома с указанием позиционной точки.

Изображением числа X в К-ичной системе счисления является запись вида:

а_nа_n-1...а₁а₀.а_-1...а _-т... _-к

где а_i- любая буква алфавита данной системы счисления,

количество букв в К-ичной системе счисления равно К.

Упорядоченной последовательности букв алфавита приписываются базисные числа: последовательные целые числаот нуля до К-1 включительно, 0 ≤ |а_i| ≤ К-1, поскольку только в этом случае любое число Х может быть представлено в виде полинома.

Двоичная система счисления

В современной вычислительной технике, в устройствах автоматики и связи широко используется двоичная система счисления. Это система счисления с наименьшим возможным основанием. В ней для изображения числа используются только две цифры: 0и 1.

Двоичная система удобна потому, что:

простота технической реализации

простота арифметических операций

простота шифрования.

Система неудобна из-за громоздкости записи чисел. Однако для ЭВМ этот факт не имеет существенного значения

Арифметические операции в двоичной системе счисления

Постановка задачи перевода чисел из одной системы счисления в другую

При решении задач с помощью ЭВМ исходные данные обычно задаются в десятичной системе счисления; в этой же системе, как правило, нужно получить и окончательные результаты.

При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только такими системами счисления, у которых базисными числами являются последовательные целые числа от 0 до Р-1 включительно, где Р— основание системы счисления.

Пусть известна запись числа Х в системе счисления с каким-либо основанием Р:
p_np_n-1...p₁p₀.p_-1...p_-т...

где p_i – известные буквы, 0 ≤ |p_i| ≤ P-1.

Требуется найти запись этого же числа X в системе счисления с основанием Q:
q_nq_n-1...q₁q₀.q_-1...q_-т...

где q_i– искомые буквы, 0 ≤ |q_i| ≤ Q-1

Перевод целых чисел

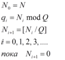
Перевод дробных чисел

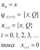
Понятие смешанной системы счисления

В ряде случаев числа, заданные в СС с основанием P, приходится изображать с помощью цифр другой СС с основанием Q, где Q<P.

Такая ситуация возникает, например, когда в ЭВМ, способной непосредственно воспринимать только двоичные числа, необходимо изобразить десятичные числа, с которыми мы привыкли работать.

В этих случаях используются смешанные системы счисления, в которых каждый коэффициент Р-ичного разложения числа записывается в Q-ичной системе.

В такой системе P называется старшим основанием, Q – младшим, а сама система называется
(Q-P)-ичной.

Условие однозначности записи чисел в смешанной системе счисления

Для того чтобы запись числа в смешанной системе счисления была однозначной, для представления любой Р-ичной цифры отводится одно и то же количество Q-ичных разрядов, достаточное для представления любого базисного числа Р-ичной системы.

Условимся изображать принадлежность числа к (Q - Р)-ичной системе счисления с помощью нижнего индекса (Q - Р) при данном числе, например
925₁₀ = 1001 0010 0101_{(2 – 10)}

Двоично-десятичная система

В смешанной двоично-десятичной системе счисления для изображения каждой десятичной цифры отводится 4 двоичных разряда.

Например, десятичное число х =729 в двоично-десятичной системе запишется в виде 0111 0010 1001. Здесь последовательные четверки (тетрады) двоичных разрядов изображают цифры
7, 2, 9 записи числа в десятичной системе.

Еще пример: 925₁₀ = 1001 0010 0101_{(2 – 10)}

Заметим, что 100100100101₂ = 2341₁₀

Двоично-шестнадцатеричная система

Двоично-шестнадцатеричная система: 2E.9₁₆ = 0010 1110.1001_(2-16)

Свойство смешанных систем и использование его в практических целях

Особого внимания заслуживает случай, когда Р = Q^l, где / — целое положительное число.

В этом случае запись какого-либо числа в смешанной системе тождественно совпадает с изображением этого числа в системе счисления с основанием Q(что не имеет места в двоично-десятичной системе в общем случае).

Двоично-восьмеричная система 57.5₈ =101 111.101 _(2-8) = 101111.101 ₂

Двоично-шестнадцатеричная система 2E.9₁₆ = 0010 1110.1001_(2-16) = 101110.1001₂

Двоично-четверичная система 232.3₄= 10 11 10. 11 _(2-4) = 101110.11 ₂

Рассмотренное выше свойство используется на практике для сокращенной записи чисел, заданных в системе счисления с небольшим основанием.

Для этого в исходной записи числа разряды объединяются вправо и влево от точки в группы длиной l (добавляя в случае необходимости левее старшей или правее младшей значащих цифр соответствующее количество нулей), и каждая такая группа записывается одной цифрой другой системы, основание которой равно соответствующей степени l исходного основания.

Цели кодирования информации

Цели кодирования информации

Формирование представления информации называется еекодированием. В более узком смысле под кодированием понимается

переход от исходного представления информации, удобного для восприятия человеком, к представлению, удобному для хранения, передачи и обработки. В этом случае обратный переход к исходному представлению называется декодированием.

При кодировании информации ставятся следующие цели:

удобство физической реализации;

удобство восприятия;

высокая скорость передачи и обработки;

экономичность, т.е. уменьшение избыточности сообщения;

надёжность, т.е. защита от случайных искажений;

сохранность, т.е. защита от нежелательного доступа к информации.
Эти цели часто противореч<