Распределение F Фишера-Снедекора.

Если U V – независимые случайные величины, распределённые по закону 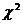со степенями свободы k₁ и k₂ , то величина имеет распределение, которое называют распределением F Фишера-Снедекора со степенями свободы k₁ и k₂ (иногда его обозначают через )

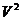Показательное распределение.

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X которое описывается плотностью при где 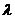- постоянная положительная величина.

Гамма-распределение.

Неотрицательная случайная величина X имеет гамма-распределение, если её плотность распределения выражается формулой 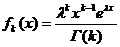где 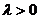и k>0, Г(k) – гамма-функция:

Таким образом, гамма-распределение является двухпараметрическим распределением, оно занимает важное место в математической статистике и теории надёжности. Это распределение имеет ограничение с одной стороны

60. Распределение Эрланага k-го порядка.

(x>0;k=1,2,3…)

Функция надёжности.

Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы элемента за время t: R(t)=P(T>t)=1-F(t)

Показательным законом надёжности называют функцию надёжности определяемую равенством 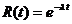где 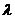- интенсивность отказов.

Система двух случайных величин.

Совокупность двух случайных величин (X,Y), рассматриваемых совместно, называется системой двух случайных величин, геометрически интерпретируется как случайная точка с координатами (X,Y) на плоскости xOy или как случайный вектор, направленный из начала координат.

Величины, возможные значения которых определяются двумя, тремя, …, n числами, называют соответственно двумерными, трехмерными, … n-мерными.

Закон распределения вероятностей дискретной двумерной случайной величины.

Называют перечень возможных значений этой величины, то есть пар чисел x­_i,y_j и их вероятностей p(x_i,y_i)(i=1,2,…,n; j=1,2,…m). Обычно закон распределения задают в виде таблицы СС двойным входом.

Первая строка таблицы содержит все возможные значении составляющей X, а первый столбец – все возможные составляющей Y. В клетке, стоящей на пересечении «столбца x_i» и «строки y_i», указана вероятность p(x_i,y_i) того, что двумерная случайная величина примет значение (x_i­,y_i)

64. Функция распределения двумерной случайной величины(X,Y).

Называют функцию F(x,y), определяющую для каждой пары чисел x,y вероятность того, что X примет значение , меньшее x, и при этом , Y примет значение, меньшее y: F(x,y)=P(X<x,Y<y).

65. Плотность совместного распределения вероятностей f(x,y).

Двумерной непрерывной случайной величины (X,Y) называют вторую смешанную частную производную от функции распределения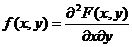

Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.