Функция одного случайного аргумента

Функция Y называется функцией случайного аргумента X, если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то есть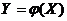

Если X – дискретная случайная величина, то

1. Если различным значения аргумента X соответствуют различные возможные значения функции Y, то вероятности соответствующих значений X и Y равны между собой.
2. Если различным возможным значениям X соответствуютзначения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.

Если аргумент X – непрерывная случайная величина, тогда если 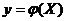- дифференцируемая строго возрастающая или строго убывающая функция которой 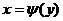, то плотность распределения 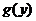случайной величины Y находится с помощью равенства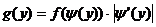

Функция двух случайных аргументов

Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z , то Z называют функцией случайных аргументов X и Y: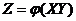

Для дискретных независимых случайных величин, чтобы составит закон распределения Z=X+Y­, надо найти все возможные значения Z и их вероятности.

Для непрерывных случайных величин плотность распределения может быть найдена с помощью равенства 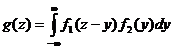либо с помощью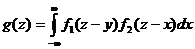

f₁ и f₂ - плотности распределения аргументов.

53. Закон равномерного распределения вероятностей.!!!

Распределении вероятностей равномерное , если на интервале, которому принадлежат все возможные значения случайной величины плотность распределения сохраняет постоянно значение

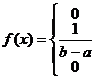при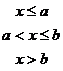

Нормальное распределение вероятностей.

Нормальным называют распределение вероятностей непрерывной случайной величины, которая описывается плотностью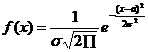

Нормальное распределение определяется двумя параметрами:

a – математическое ожидание

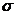- среднее квадратическое отклонение нормального распределения

Если a=0 и 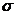=1, то нормальное распределение называют нормированным.

Функция распределения Ф(x) общего нормального распределения равна: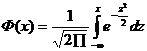

Распределение «хи-квадрат».

Пусть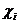(i=1,2,…n) – нормальные независимые случайные величины, причём математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение - единице. Тогда сумма квадратов этих величин распределена по закону 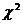«хи-квадрат» с k=n степенями свободы; если же эти величины связаны одним линейным соотношением, например 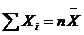то число степеней свободы k=n-1

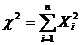
Распределение Стьюдента.

Пусть Z –нормальная случайная величина, приём M(Z)=0, 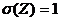а V –независимая от Z величина, которая распределена по закону 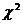с k степенями свободы. Тогда величина 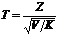имеет распределение, которое называют t-распределением или распределением Стьюдента с k степенями свободы.