Произведение нескольких событий.

Произведением нескольких событий называют событие, состоящее в совместном появлении этих

событий.

Испытания независимые относительно одного события.

Пусть вероятность события B не зависит от появления события A.

Событие B называют независимым от события A, если появление события A не изменят вероятности события B, то есть если условная вероятность события B равна его безусловной вероятности:

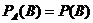
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противоположном случае события называют зависимыми

Теорема умножения событий.

Для независимых событий теорема умножения P(АВ) = P(А)*PA(B) имеет вид P(AB) = P(A)*Р(B), т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Условная вероятность.

Условной вероятностью 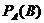называют вероятность события B, вычисленную в предположении, что событие A уже наступило.

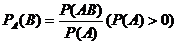
Вероятность совместного появления двух событий.

Теорема Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого вычисленную в предположении, что первое событие уже наступило:

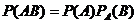
Вероятность появления хотя бы одного события.

Вероятность появления хотя бы одного из событий A_1,A₂,…,A_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий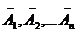

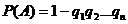
Сложное событие.

Это совмещение нескольких отдельных событий, которые называются простыми

Простое событие – это результат испытания

Дискретная случайная величина.

Случайной называю величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайная величина называется дискретной, если она может принимать только конечное или счётное множество возможных значений. Дискретные случайные величины, которые могут принимать лишь целые неотрицательные значения, называются целочисленными и возникают при каких-то подсчётах.

Непрерывная случайная величина.

Случайная величина называется непрерывной, если она может принимать любое значение из некоторого интервала, причём этот интервал может быть ограниченным или неограниченным. Непрерывная случайная величина имеет несчётное множество значений, которые сплошь заполняют некоторый интервал числовой оси или всю ось. Возникает при изменении отклонения контрольного параметра изделия массового производства от её номинального значения, при изменении расстояния от центра цели до точки падения снаряда.