Программа сложения столбцов определителя
Контрольный пример:
Сложение 2-го и 3-го столбцов с помещением результата на место 2-го
Исходный определитель Результат



 6 3 0 3 6 3 0 3
6 3 0 3 6 3 0 3
4 2 2 1 4 4 2 1
0 0 4 2 0 4 4 2
7 -1 8 5 7 7 8 5
Вариант 22
Программа вычитания строк определителя
Контрольный пример:
Вычитание из 1-ой строки 2-ой строки с помещением результата на место
2-ой строки
Исходный определитель Результат



 6 3 0 3 6 3 0 3
6 3 0 3 6 3 0 3
4 2 2 1 2 1 -2 2
0 0 4 2 0 0 4 2
7 -1 8 5 7 -1 8 5
Вариант 23
Программа вычитания столбцов определителя с умножением
Контрольный пример:
Вычитание из 2-го столбца 3-го, умноженного на –1, с помещением результата на место 2-го
Исходный определитель Результат



 6 3 0 3 6 3 0 3
6 3 0 3 6 3 0 3
4 2 2 1 4 4 2 1
0 0 4 2 0 4 4 2
7 -1 8 5 7 7 8 5
Вариант 24
Программа сложения строк определителя с умножением
Контрольный пример:
Сложение 1-ой и 2-ой строки, умноженной на –1, с помещением результата на место 2-ой строки
Исходный определитель Результат



 6 3 0 3 6 3 0 3
6 3 0 3 6 3 0 3
4 2 2 1 2 1 -2 2
0 0 4 2 0 0 4 2
7 -1 8 5 7 -1 8 5
Варианты 21-24.
Размерность определителя n вводится посредством оператора INPUT. Для ввода определителя и вывода его на экран организуется двойной (вложенный) цикл FOR…NEXT. Следует предусмотреть ввод элементов определителя с клавиатуры (INPUT) и с помощью генератора случайных чисел RND(1) – автоматический ввод. Вывод на экран организовать следующим образом (вариант 24):
6 3 0 3
4 2 2 1
0 0 4 2
7 –1 8 5
Какую строку сложить (номер) = 1
С какой строкой (номер) = 2
Введите множитель = -1
6 3 0 3
2 1–2 2
0 0 4 2
7 –1 8 5
После указания номеров строк и ввода множителя организуется перезапись определителя с заменой элементов 2-й строки (для данного контрольного примера) на соответствующую сумму элемента 1-й строки и элемента 2-й, умноженного на множитель. Очевидно, что для помещения результата на 1-у строку необходимо было ввести сначала номер 2, а затем 1. Следует предусмотреть возможность продолжения работы, чтобы складывать другие строки с другим множителем. Например, INPUT "Продолжить работу, да – Enter, нет – 1 ", v
IF v = 0 THEN 90 ELSE 600 'на END
где 90 – номер строки с вопросом о номере слагаемой строки определителя.
Вариант 25
Программа поиска целочисленных решений уравнения ax + by = c
Пусть c = 100
Вариант 26
Программа поиска целочисленных решений уравнения ax + by + cz = d
Пусть d = 100
Вариант 27
Программа поиска целочисленных решений уравнения x2 + y2 = z2.
(программа поиска пифагоровых чисел)
Пусть граница перебора = 30.
Варианты 25-27
После ввода коэффициентов уравнения (a, b, c, d – для варианта 26) посредством оператора INPUT, определяются границы перебора. Например, граница перебора по x будет nx = INT(1 + (d – b – c) / a). Аналогично определяются другие границы перебора в варианте 26 и 25. А для варианта 27 граница перебора задается с помощью оператора INPUT. Затем для перебора значений x, y, z в заданных пределах организуется тройной (вложенный) цикл, а для варианта 25 – двойной. При выполнении соответствующего условия значения переменных (вариант 26) выводятся на экран в следующем виде:
Целочисленные решения уравнения 5x + 11y +17z = 100
x = 1 y = 4 z = 3
x = 2 y = 2 z = 4
x = 10 y = 3 z = 1
x = 11 y = 1 z = 2
В соответствующих случаях выводится сообщение: Решений нет.
Вариант 28
Программа перевода 10-тичного числа в 2-ичную систему
Пример. Найти двоичное представление для числа А(10) = 43(10) =
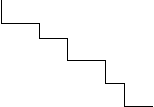
|
Вариант 29
Программа перевода 10-тичного числа в 8-ричную систему
Пример. Найти 8-ричное представление для числа А(10) = 43(10) =
= к1к0 - искомое 8-ричное представление 43(10) = 53(8)
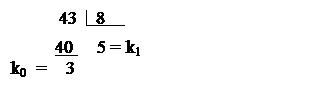
Вариант 30
Программа перевода 10-тичного числа в 16-ричную систему
Пример. Найти 16-ричное представление для числа А(10) = 540(10) =
= к2к1к0 - искомое 16-ричное представление 540(10) = 21С(16)
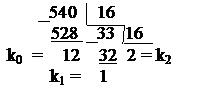 10 – А 13 – D
10 – А 13 – D
11 – В 14 – E
12 – С 15 – F
Варианты 28-30
Десятичное число и основание счисления вводятся посредством оператора INPUT. В основе процедуры перевода числа из одной системы счисления в другую лежит процедура целочисленного деления переводимого числа на основание счисления p. При этом определяется остаток от деления, дающий цифры искомого числа (его удобно получать с помощью функции a MOD p) и частное, для последующего деления на основание счисления. Рекомендуется использовать целочисленное деление посредством обратного слеша \. Процедура заканчивается когда делимое станет меньше делителя (дает первую цифру искомого числа). Для организации цикла лучше использовать циклический оператор DO…LOOP. Вывод на экран осуществлять, используя PRINT USING "#"; a(i). Для вариантов 29-30 предусмотреть проверку с помощью операторов OCT$(n) и HEX$(n), соответственно. Вывод на экран:
765(10) = 2FD(16)
Вариант 31
