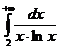Л.Н. Ларина, Р.П. Лазарева, Г.Е. Юдина.
«Контрольные задания с методическими рекомендациями» по курсу высшей математики: Методическое пособие. – Альметьевск: Альметьевский государственный нефтяной институт, 2009. – 124 с.
Методическое пособие «Контрольные задания с методическими рекомендациями» по курсу высшей математики. Часть II предназначенное для изучения соответствующих разделов высшей математики для студентов всех специальностей заочной формы обучения. Пособие содержит решённые примеры, 30 вариантов контрольных работ.
Печатается по решению учебно-методического совета АГНИ.
Рецензенты:
Декан ФИМ, зав кафедрой «ТХНГ», д.т.н., профессор М.М. Алиев
Зав. кафедрой информатики, к.п.н., доцент Иванов А.Ф.
© Альметьевский государственный
нефтяной институт, 2009
Оглавление.
1. Введение. Правила выполнения и оформления контрольных работ.
2. Контрольная работа №5. Интегральное исчисление функции одной действительной переменной.
3. Контрольная работа №6. Дифференциальные уравнения.
4. Контрольная работа №7. Ряды. Кратные интегралы.
5. Контрольная работа №8. Теория функций комплексного переменного.
6. Контрольная работа №9. Криволинейные и поверхностные интегралы. Элементы теории поля.
7. Контрольная работа №10. Теория вероятностей.
ВВЕДЕНИЕ
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4-5 см для замечаний рецензента.
2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента. В конце работы следует поставить дату ее выполнения и подпись студента.
3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.
4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые рисунки.
7. После получения прорецензированной работы, как незачтенной так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Контрольная работа №5
Интегральное исчисление функции одной действительной переменной.
I. Вычислить неопределенный интеграл (а – ж).
II. Вычислить определенный интеграл.
III. Решить задачу на приложения определенного интеграла.
IV. Показать расходимость или вычислить несобственный интеграл.
Вариант 1
I.a) 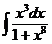 б)
б) 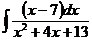 в)
в) 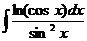
г) 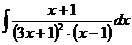 д)
д) 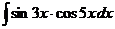 е)
е) 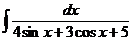
ж) 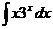
II. 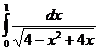
III.Найти площадь фигуры, ограниченной линиями y = x2; y = 6 - x; y = 0.
IV. 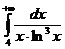
Вариант 2
I.а) 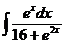 б)
б) 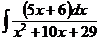 в)
в) 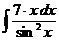 г)
г) 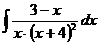
д) 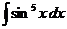 е)
е) 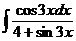 ж)
ж) 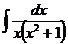
II. 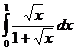
III.Найти площадь фигуры, ограниченной линией r = 4cos2 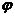 .
.
IV. 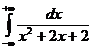
Вариант 3
I.а) 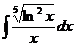 б)
б) 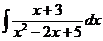 в)
в) 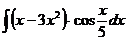 г)
г) 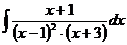
д) 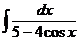 е)
е)  ж)
ж) 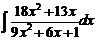
II. 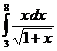
III.Найти объем тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: y = 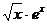 ; x = 1; y = 0.
; x = 1; y = 0.
IV. 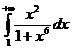
Вариант 4
I.a) 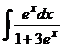 б)
б) 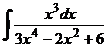 в)
в) 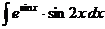 г)
г) 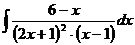
д) 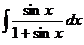 е)
е) 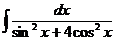 ж)
ж) 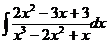
II. 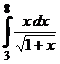
III.Найти длину дуги линии: y=lnsin x 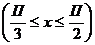
IV. 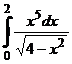
Вариант 5
I.a) 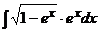 б)
б) 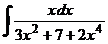 в)
в) 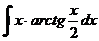 г)
г) 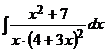
д) 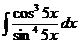 е)
е) 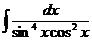 ж)
ж) 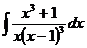
II. 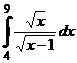
III.Найти площадь фигуры, ограниченной линиями y = 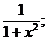 y =
y = 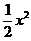 .
.
IV. 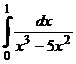
Вариант 6
I.a) 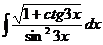 б)
б)  в)
в) 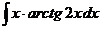 г)
г) 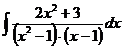
д) 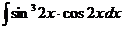 е)
е) 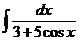 ж)
ж) 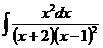
II. 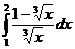
III.Найти длину кардиоиды r = 3(1 - cosj).
IV. 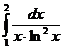
Вариант 7
I.a) 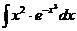 б)
б) 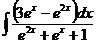 в)
в)  г)
г) 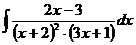
д) 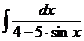 е)
е) 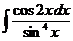 ж)
ж) 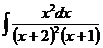
II. 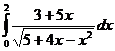
III.Окружность х2 + у2 = 8 разделена параболой 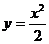 на две части. Найти площадь «внутри» параболы.
на две части. Найти площадь «внутри» параболы.
IV. 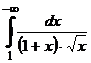
Вариант 8
I.a) 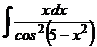 б)
б) 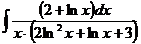 в)
в) 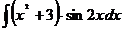
г) 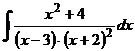 д)
д) 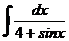 е)
е) 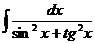
ж) 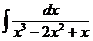
II. 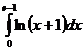
III.Найти длину дуги линии 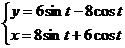 от t = 0 до t =
от t = 0 до t = 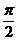
IV. 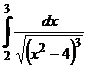
Вариант 9
I.a) 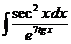 б)
б) 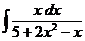 в)
в)  г)
г) 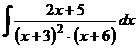
д) 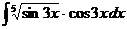 е)
е) 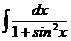 ж)
ж) 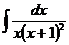
II. 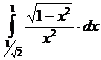
III.Найти объем тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями у = 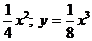
IV. 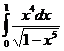
Вариант 10
I.а) 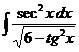 б)
б) 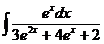 в)
в) 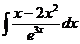 г)
г) 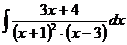
д) 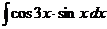 е)
е) 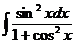 ж)
ж) 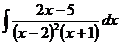
II. 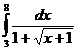
III.Вычислить площадь фигуры, ограниченной параболами у = 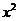 и у =
и у = 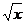 .
.
IV. 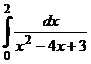
Вариант 11
I.а) 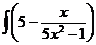
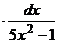 б)
б) 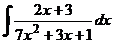 в)
в) 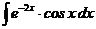 г)
г) 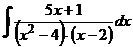
д) 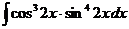 е)
е) 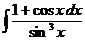 ж)
ж) 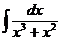
II. 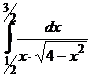
III.Вычислить площадь фигуры, ограниченной осью ординат и линиями у = sinx; y = cosx.
IV. 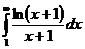
Вариант 12
I.а) 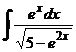 б)
б) 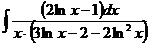 в)
в) 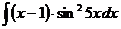
г) 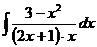 д)
д) 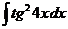 е)
е) 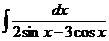 ж)
ж) 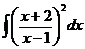
II. 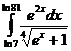
III.Найти длину дуги линии y = 1 - ln 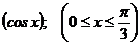 .
.
IV. 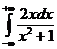
Вариант 13
I.а) 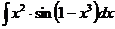 б)
б) 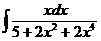 в)
в) 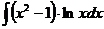
г) 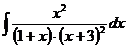 д)
д) 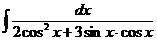 е)
е) 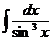 ж)
ж) 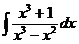
II. 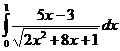
III.Найти объем тела вращения вокруг оси ох линии у = хex, ограниченной прямыми у = 0; х = 1.
IV. 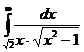
Вариант 14
I.а) 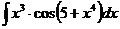 б)
б) 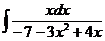 в)
в) 
г) 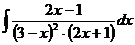 д)
д) 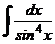 е)
е) 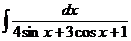 ж)
ж) 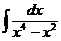 7
7
II. 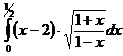
III.Вычислить площадь фигуры ограниченной линиями: 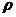 =5сos
=5сos 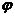
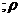 =10 cos
=10 cos 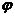 .
.
IV. 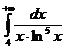
Вариант 15
I.а) 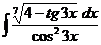 б)
б) 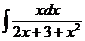 в)
в) 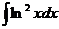 г)
г) 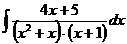
д) 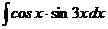 е)
е) 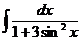 ж)
ж) 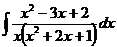
II. 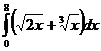
III.Найти площадь фигуры, ограниченной улиткой Паскаля r = 2а 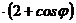 .
.
IV. 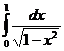
Вариант 16
I.а) 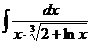 б)
б) 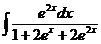 в)
в) 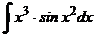 г)
г) 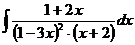
д) 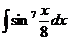 е)
е) 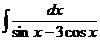 ж)
ж) 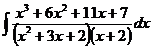
II. 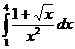
III.Найти площадь, ограниченную трехлепестковой розой r = acos3 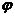 .
.
IV. 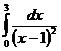
Вариант 17
I.а) 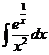 б)
б) 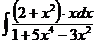 в)
в) 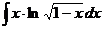 г)
г) 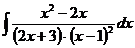
д) 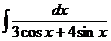 е)
е) 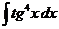 ж)
ж) 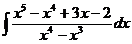
II. 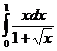
III.Вычислить длину астроиды x = аcos 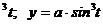 .
.
IV. 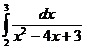
Вариант 18
I.а) 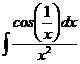 б)
б) 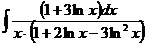 в)
в) 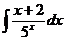
г) 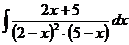 д)
д) 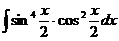 е)
е) 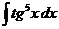
ж) 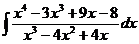
II. 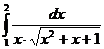
III.Найти длину дуги кривой y = 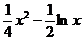 , 1
, 1 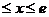 .
.
IV. 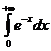
Вариант 19
а) 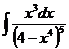 б)
б) 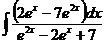 в)
в) 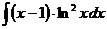 г)
г) 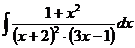

д) 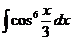 е)
е) 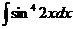 ж)
ж) 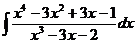
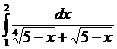
Найти длину дуги полукубической параболы y = 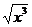 от начала координат до точки В(4,8).
от начала координат до точки В(4,8).
Вариант 20
I.а) 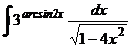 б)
б) 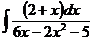 в)
в) 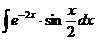 г)
г) 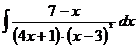 д)
д) 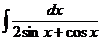 е)
е) 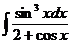 ж)
ж) 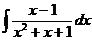
II. 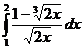
III.Найти площадь одного лепестка кривой r = 4sin 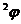 .
.
IV. 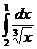
Вариант 21
I.а) 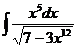
 б)
б) 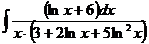 в)
в) 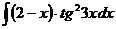
г) 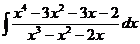 д)
д) 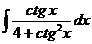 е)
е) 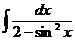 ж)
ж) 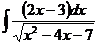
II. 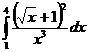
III.Вычислить площадь, ограниченную одной полуволной синусоиды y = sinx и осью оx.
IV. 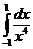
Вариант 22
I.а) 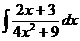 б)
б) 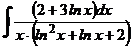 в)
в)  г)
г) 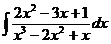
д) 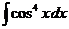 е)
е) 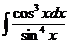 ж)
ж) 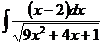
II. 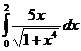
III.Найти площадь, ограниченную параболой y = 4x – x2 и прямой у = х+2.
IV. 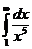
Вариант 23
I.а) 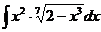 б)
б) 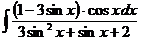 в)
в)  г)
г) 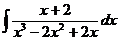
д) 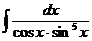 е)
е) 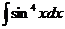 ж)
ж) 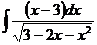
II. 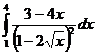
III.Найти площадь, ограниченную кривыми y = e 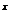 и y = e
и y = e 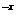 и прямой x = 1.
и прямой x = 1.
IV. 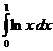
Вариант 24
I.а) 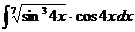 б)
б) 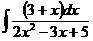 в)
в) 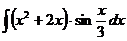 г)
г) 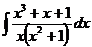
д) 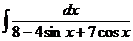 е)
е) 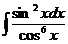 ж)
ж) 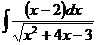
II. 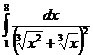
III.Найти площадь, ограниченную кривой у = 4x – x2 и осью оx.
IV. 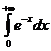
Вариант 25
I.а) 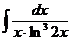 б)
б) 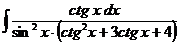 в)
в) 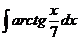 г)
г) 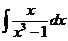
д) 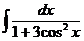 е)
е)  ж)
ж) 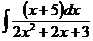
II. 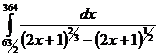
III.Найти площадь эллипса, используя его параметрические уравнения x = acost, y = вsint.
IV. 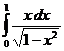
Вариант 26
I.а) 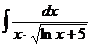 б)
б) 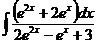 в)
в) 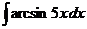 г)
г) 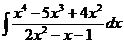
д) 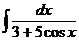 е)
е) 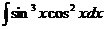 ж)
ж) 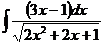
II. 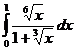
III.Найти площадь, ограниченную параболой y = x2 и прямой y = –2x +3.
IV. 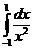
Вариант 27
I.а) 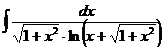 б)
б) 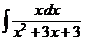 в)
в) 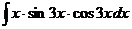
г) 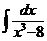 д)
д) 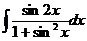 е)
е) 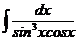
ж) 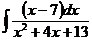
II. 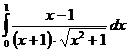
III.Найти длину дуги кривой y = lnx от x = 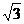 до x =
до x = 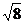 .
.
IV. 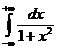
Вариант 28
I.а) 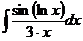 б)
б) 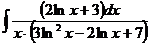 в)
в) 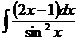 г)
г) 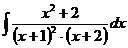
д) 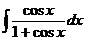 е)
е) 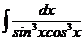 ж)
ж) 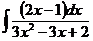
II. 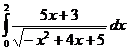
III.Найти объем тела, образованного вращением вокруг оси ox фигуры, ограниченной параболой y = x2 , осью oy и прямой y = 1.
IV. 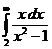
Вариант 29
I.а) 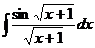 б)
б) 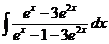 в)
в) 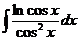 г)
г) 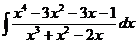
д) 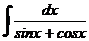 е)
е) 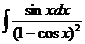 ж)
ж) 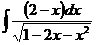
II. 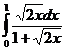
III.Вычислить объем тела вращения вокруг оси ох одной полуволны синусоиды у = sin2x ( 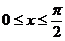 ).
).
IV. 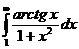
Вариант 30
I.а) 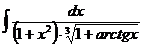 б)
б) 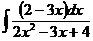 в)
в) 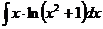 г)
г) 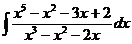
д) 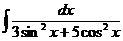 е)
е) 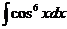 ж)
ж) 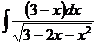
II. 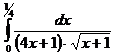
III.Найти площадь фигуры, ограниченной первой аркой циклоиды x = a(t - sint), y = a(1 - cost), (tÎ[0;2π]) и осью абсцисс.
IV.