Образец выполнения контрольной работы №1.

Задание 1. Найти матрицу, обратную к матрице

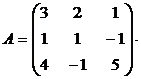
Решение:

1) Вычислим определитель матрицы А:

.

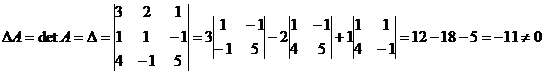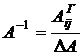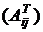2) Обратная матрица А^-1 вычисляется по формуле , где – транспонированная матрица, составленная из алгебраических дополнений.

а) Найдем алгебраические дополнения всех элементов матрицы

; ;

; ;

; ; .

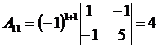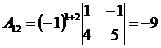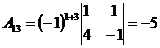
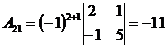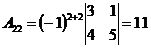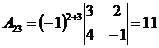
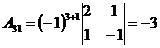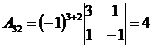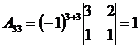б) Составим матрицу алгебраических дополнений

.

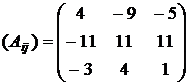в) Транспонируем матрицу 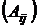, получим .

.

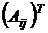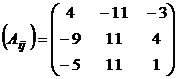г) Вычисляем обратную матрицу

.

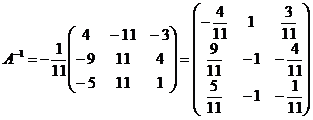д) Для проверки умножим А^-1 на А,

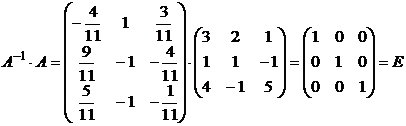
Ответ: .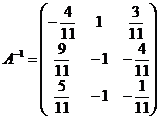

Задание 2. Дана система линейных алгебраических уравнений (СЛАУ)

.

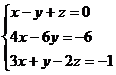Доказать ее совместимость и решить тремя способами:

1. методом Гаусса;

2. по формулам Крамера;

3. средствами матричного исчисления.

Решение:

1. Метод Гаусса заключается в последовательном исключении неизвестных и осуществляется в два этапа:

а) прямой ход заключается в приведении системы к ступенчатому (треугольному) виду (при этом последнее уравнение системы имеет одну неизвестную); б) Обратный ход заключается в последовательном определении неизвестных из уравнений системы.

С помощью элементарных преобразований над строками расширенной матрицы системы сведем ее к треугольному виду. Если в процессе СЛАУ методом Гаусса какая-либо строка примет вид 0=0, это будет свидетельствовать о том, что СЛАУ имеет бесконечное множество решений, если же возникает строка 0 = const, то система несовместна.

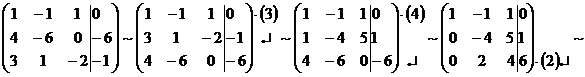
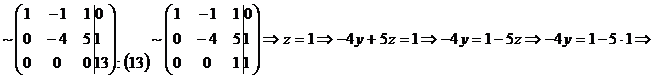
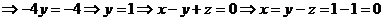. Ответ: (0,1,1).

2. Формулы Крамера.

При 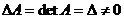СЛАУ совместна и имеет единственное решение, которое может быть найдено по формулам Крамера 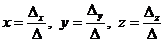, где ∆ - определитель матрицы А системы, а ∆_х, ∆_у, ∆_z – определители для неизвестных (х,у,z), полученные заменой соответствующего столбца, составленного из коэффициентов при неизвестных, на столбец свободных членов.

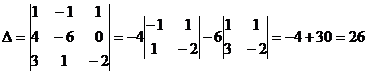
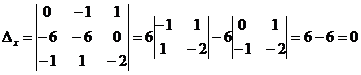
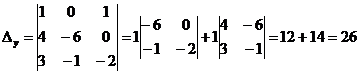
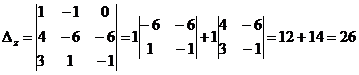
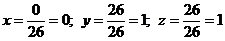. Ответ: (0,1,1).

3. Матричный метод.

СЛАУ удобно записать в матричной форме А·Х=С, где А – матрица системы, Х – столбец неизвестных членов, С – столбец свободных членов.

Из матричного уравнения следует Х = А^-1С, (*) где А^-1 – обратная матрица, которая вычисляется по формул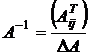е , где 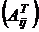– транспонированная матрица, составленная из алгебраических дополнений.

Вычислим определитель матрицы А (смотрите выше)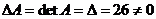

а) Найдем алгебраические дополнения всех элементов матрицы

; ;

; ;

; ;

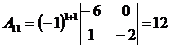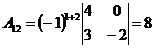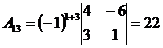
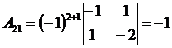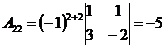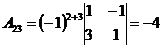
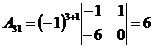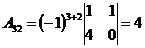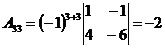
б) Составим матрицу алгебраических дополнений

.

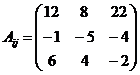в) Транспонируем матрицу А_ij и получим А_ij^Т

.

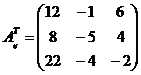г) Вычисляем обратную матрицу

.

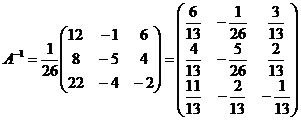Согласно формуле (*) столбец решений

.

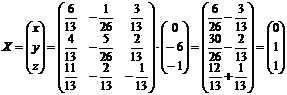Таким образом, СЛАУ: х = 0, у = 1, z = 1, что подтверждается в ходе проверки (подстановки полученных значений в каждое уравнение системы).

Задание 3. Даны вершины треугольника АВС: А(1;-1;2), B(5;-6;2), С(1;3;-1). Найти длину его высоты, опущенной из вершины В на сторону АС.

Решение: Площадь S треугольника АВС равна половине площади параллелограмма, построенного на векторах 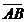и 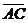, то есть 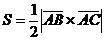. Имеем: 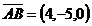, 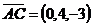. Тогда векторное произведение этих векторов равно .

(*).

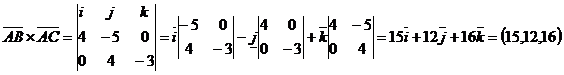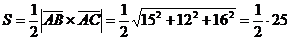Известно, что площадь треугольника равна (**).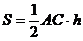

Из равенств (*) и (**) и определим высоту h

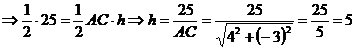. Ответ: h = 5.

Задание 4. Даны координаты вершин пирамиды А₁А₂А₃А₄

А₁ (2; -1; 1), А₂ (5; 5; 4), А₃ (3; 2; 3), А₄ (4; 1; 3). Найти:

1) длину ребер A₁A₂; A₁A₃; A₁A₄;

2) угол между ребрами: A₁A₂ и A₁A₄;

3) площадь грани A₁A₂А₃;

4) объем пирамиды;

5) длину высоты, опущенной из вершины А₄ на грань A₁A₂А₃.

Решение:

1) ,

,

,

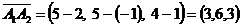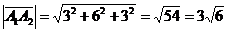
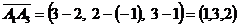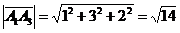
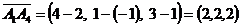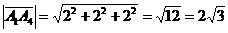
2) Пусть α угол между ребрами A₁A₂ и A₁A₄. Скалярное произведение векторов 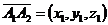и 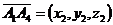запишется в следующем виде:

.

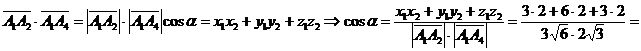
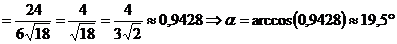3) Площадь грани A₁A₂А₃ вычислим, исходя из геометрического смысла векторного произведения векторов. Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах. Площадь треугольника A₁A₂А₃ равна половине площади треугольника .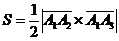

.

.

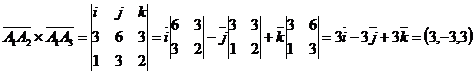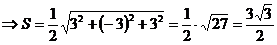4) Объем пирамиды численно равен 1/6 модуля смешанного произведения векторов, образующих данную пирамиду, то есть 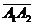, 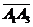и .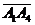

.

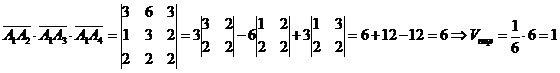5) Известно, что 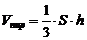, где S – площадь основания (грань A₁A₂А₃) пирамиды, а h – высота пирамиды, проведенная из вершины А₄ на грань A₁A₂А₃. .

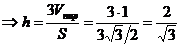Контрольная работа №2