Коэффициент удельного скольжения l.

Характеризует износостойкость зубчатой передачи в высшей КП.

4.5.3 Определение коэффициента перекрытия графическим способом.

B₁B₂ рабочий участок линии зацепления N₁N₂.

В точке В₁ пара эвольвент входит в зацепление, при повороте на угол t₁=360^о/z₁ первая пара эвольвент касается в т. К, а в т.В₁ в зацепление вошла следующая пара эвольвент, и участок КВ₂ обе пары эвольвент проходят вместе, т.е. вторая пара эвольвент перекрывает работу первой пары. Тогда e_a равен

e_a = ,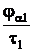

где j_a1 – угол перекрытия первого колеса.

j_a1 = r_b1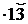

e_a =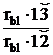

Т.к. линия зацепления перекатывается по основной окружности без скольжения, то

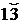= B₁B₂ , =B₁K

e_a =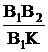

§4.6 Способы изготовления зубчатых колес

Существуют два основных способа изготовления зубчатых колес:

1. копирование: профиль зуба инструмента (протяжка) переносится, и он оставляет след. Способ очень неточный, малопроизводительный и требует наличие инструмента в большом ассортименте, различаемых по модулю и количеству зубьев. Применяется в мелко серийном производстве.

2. огибание (см. лаб.раб. №8): инструменту и заготовке сообщают такое относительное движение, при котором огибающая к положению режущей кромке инструмента очерчивает эвольвенту. Инструмент может быть различным: рейки (гребенки), долбяки и фрезы.

4.6.1 Понятие о производящем исходном контуре реечного инструмента.

Производящий исходный контур – проекция режущей грани инструмента на плоскость, перпендикулярную оси вращения заготовки.

Рейка – зубчатое колесо с теоретически бесконечно большим количеством зубьев. Как привило, их бывает 8.

r_b à , поэтому все окружности и эвольвента – прямые.

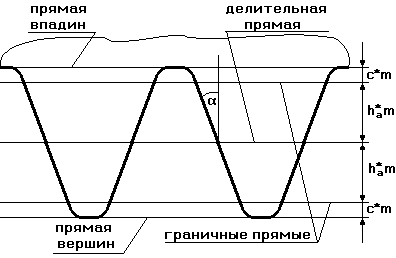
Все параметры по делительной прямой и по прямым, параллельным делительной прямой, стандартизированы.

a=20^о ;h_a* - коэффициент высоты зуба (по ГОСТ h_a*=1).

4.6.2 Станочное зацепление.

Станочное зацепление – зацепление заготовки и инструмента (см. рис. 10-86).

Параметры, относящиеся к инструменту, имеют индекс ‘_o’

e_o – ширина впадины инструмента по делительной прямой,

s_о – толщина зуба инструмента по делительной прямой.

У инструмента всегда e_o = s_o, r_wo = r.

В станочном зацеплении начальная окружность всегда совпадает с делительной окружностью, т.к. необходимо перенести с инструмента стандартные параметры: шаг р, модуль m и угол профиля a. Эти стандартные параметры имеют место на делительной окружности или на прямой, параллельной делительной прямой.

По отношению к делительной окружности заготовки, делительная прямая может занимать следующие положения:

1. инструмент отодвигается от центра заготовки и между делительной окружностью заготовки и делительной прямой инструмента имеет место смещение х^.m, где х – коэффициент смещения инструмента, который имеет знак.

В рассматриваемом случае x>0, xm>0 – нарезается положительное зубчатое колесо.

Прямая инструмента, касательная к делительной окружности заготовки – станочно-начальная прямая.

2. делительная прямая инструмента является станочно-начальной прямой, т.е. касается делительной окружности. х=0, хm=0 – нулевое зубчатое колесо.

3. при смещении инструмента к центру заготовки, между делительной прямой и делительной окружностью смещение xm<0, x<0 – отрицательное зубчатое колесо.

Коэффициент изменения толщины зуба Δ:

Δ=2^.x^.tga

Вопрос: в каком диапазоне может перемещаться инструмент?

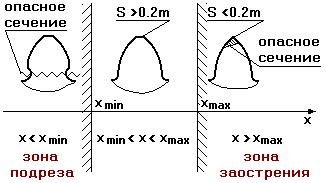
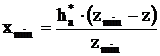
где x_min – минимальный коэффициент смещения инструмента, при котором наступает подрез зуба.

Если В₁ выйдет за N, то будет подрез ( В₁ – точка пересечения граничной прямой рейки с линией зацепления, а N – точка касания линии зацепления с основной окружностью).

ЛЕКЦИЯ 10.

z_min – минимальное количество зубьев нулевого зубчатого колеса, которое можно нарезать без подреза.

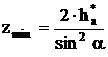
где a = 20^о , h_a^* = 1.

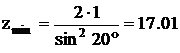
Т.к. z должно быть целым, при z_min = 18 гарантировано, что подреза не будет.

4.6.3 Основные расчетные зависимости для определения параметров зубчатого колеса, исходя из схемы станочного зацепления.

1. Радиус окружности вершин r_a.

r_a = r + xm + h_a^*m – Δуm (1)

Δуm – уравнительное смещение инструмента (расстояние между граничной прямой инструмента и окружностью вершин заготовки).

Δу вводится в расчет для того, чтобы при создании зубчатой передачи с колесами z₁ и z₂ было бы обеспечено зацепление этих колес без бокового зазора при стандартном радиальном зазоре.

2. Радиус окружности впадин r_f.

r_f = r – h_a^*m – c^*m + xm (2)

3. Определение высоты зуба.

h = r_a – r_f = 2 h_a^*m + c^*m – Δуm (3)

4. Определение коэффициента изменения толщины зуба.

Δ=2^.x^.tga

Глава 5. Специальные передаточные (планетарные) механизмы.

Планетарным называется механизм, имеющий в своем составе хотя бы одно звено с подвижной геометрической осью в пространстве.

Звено, имеющее подвижную геометрическую ось в пространстве, называется сателит.

Звено, на которое устанавливают ось сателитов, называется водило (Н).

Зубчатые колеса, имеющие неподвижную геометрическую ось в пространстве, называются центральными.

Центральное колесо, имеющее внешние зубья, называется солнечное колесо.

Центральное колесо, имеющие внутренние зубья, называется коронная шестерня (опорное колесо).

Достоинства планетарных передач:

1. имеют малые габариты и вес из-за того, что поток мощности, подводимый к центральному колесу, распределяется по к сателитам (к – количество сателитов). Затем поток мощности собирается на выходном звене. На одной планетарной передаче можно поставить до 24 сателитов.

2. очень высокий КПД, в среднем 0.99.

Недостатки:

Если число сателитов неравно 3, то необходим специальный механизм, который бы выравнивал нагрузку между сателитами. Этот механизм утяжеляет и удорожает конструкцию.

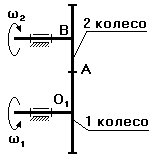
§5.1 Сравнительный анализ передачи с неподвижными осями планетарной передачи.

На первое колесо подается крутящий момент, а со второго снимают.

Ось В неподвижна Ось В подвижна

u_1-2 = 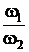= 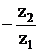u_1-Н =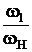

Через число зубьев u_1-Н записать нельзя, т.к. ось В – подвижная ось.

Чтобы записать передаточное отношение через число зубьев, применим метод обращения движения:

мысленно сообщим всем звеньям механизма, включая стойку, дополнительное движение с угловой скоростью -w_н. Получим обращенный планетарный механизм с неподвижными осями зубчатых колес.

В обращенном движении звенья этого механизма будут иметь следующие угловые скорости:

w₁^* = w₁ – w_Н

w₂^* = w₂ + (– w_Н) = w₂ – w_Н

w_Н^* = w_Н – w_Н = 0

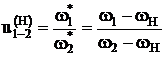- формула Виллиса

§5.2 Определение передаточного отношения планетарных механизмов различных схем.

5.2.1 Планетарный однорядный механизм (механизм Джеймса).

КПД в одном ряду – 0.99

Передаточное отношение можно определить:

1. графическим способом по чертежу;

2. аналитическим способом, используя формулу Виллиса.

Графический способ определения передаточного отношения.

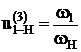
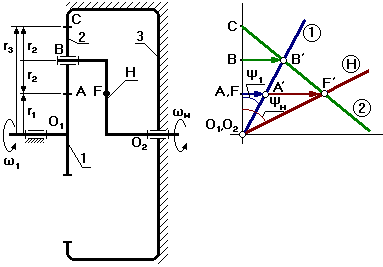
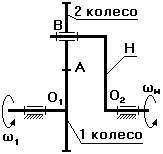
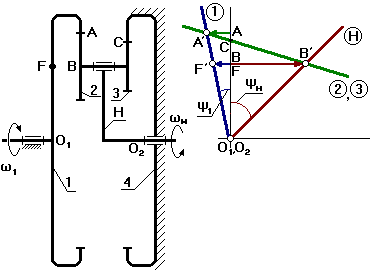
Выберем на водиле Н точку F которая расположена на том же расстоянии от оси О₂, что и точка А.

Оси О₁ и О₂ расположены на одном уровне.

Для данной схемы входное звено – звено 1 (солнечное колесо), выходным является водило Н.

Зададимся отрезком АА’, который изображает линейную скорость колеса 1 в точке А. Т.к. колесо 1 вращается вокруг О₁, то закон распределения линейной скорости по первому звену изображается прямой линией О₁А’. Сателит 2 в т.А имеет такую же линейную скорость, что и колесо 1. В т.С сателит 2 имеет МЦС в абсолютном движении, т.к. идет контакт с неподвижным колесом 3. Закон распределения линейной скорости по второму колесу изображается прямой линией СА’. В т.В сателит имеет линейную скорость, которая изображается отрезком ВВ’, однако т.В является также и осью водила Н, которое вращается вокруг О₂. Следовательно, закон распределения линейной скорости по водилу изобразиться прямой линией О₂В’. Для точки F водила линейная скорость изображается отрезком FF’.

От вертикали до линии распределения скоростей по водилу измеряем угол ψ_н, а от вертикали до линии распределения скоростей по колесу 1 измеряем угол ψ₁. Т.к. углы ψ₁ и ψ_н отложены от вертикали в одном направлении, то это показывает, что входное звено 1 и выходное звено вращаются в одном направлении.

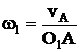
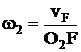
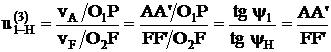
Аналитический способ определения передаточного отношения.

Применим метод обращения движения, обратив планетарный механизм в непланетарный.

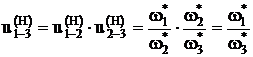
w₁^* = w₁ – w_Н

w₃^* = w₃ – w_Н = – w_Н

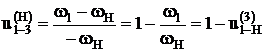
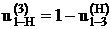
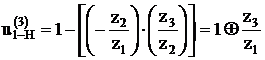– плюсовой механизм.

Лекция 11.

5.2.2 Планетарный механизм со смешанным зацеплением

(с одним внешним и одним внутренним зацеплением).

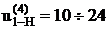при η= 0,99

Входное звено – первое звено;

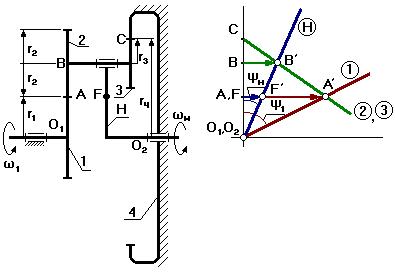Выходное – водило.

1– солнечное колесо;

2,3 – блок сателлитов;

4 – коронная шестерня;

Н – водило.

Выберем на выходном звене (на водиле) точку F так, чтобы O₁A=O₂F (O₁ и O₂ соосны).

1. Графический способ определения передаточного отношения

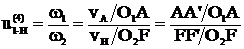
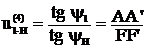
Отрезок АА' берем произвольно.

2. Аналитический способ определения передаточного отношения.

Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).

В обращенном движении каждое из звеньев будет иметь:

1 звено: ω^*₁ = ω₁ + (–ω_н)

2 звено: ω^*₂ = ω^*₃ = ω₂ + (–ω_н)

3 звено: ω^*₃ = ω^*₂ = ω₃ + (–ω_н)

4 звено: ω^*₄ = ω₄ + (–ω_н) = –ω_н

5 звено: ω^*_н = ω_н + (–ω_н) = 0

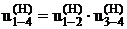(1)

если (1) переписать через количество зубьев, то

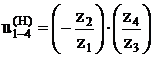
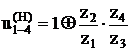
плюсовой механизм

5.2.3 Механизм с двумя внешними зацеплениями.

u⁽⁴⁾_1–Н = 20 ÷ 50 при η = 0.99

Входное звено – водило;

Выходное – первое колесо.

u⁽⁴⁾_1–Н = 1 / u⁽⁴⁾_Н–1

Например, если u⁽⁴⁾_Н–1= 20, то u⁽⁴⁾_1–Н = 1 /20 .

Графический способ.

Выберем точку F на входном звене так, чтобы O₁F = O₂B.

Точка С для данной схемы может располагаться как выше, так и ниже точки А. В зависимости от положения точки С план скоростей будет разный.

ψ₁ и φ₂ – направлены в разные стороны от вертикали. Следовательно, водило и колесо 1 вращаются в разные стороны.

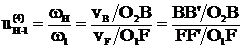
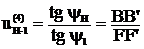
Аналитический способ.

Применим метод обращения движения.

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4

Запишем передаточное отношение через число зубьев:

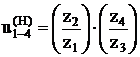
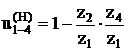
Минусовой механизм

5.2.4 Планетарный механизм с двумя внешними

зацеплениями.

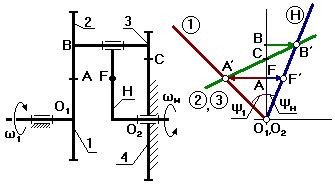
Механизм Давида

Применяется в приборных устройствах, так как u⁽⁴⁾_Н–1 до 10 000.

Недостаток – низкий К.П.Д

Графический способ.

Выберем на водиле Н точку F так, чтобы O₂F=O₁A (валы O₁ и O₂ соосны). Точка С может быть выше или ниже точки А.

FF' – произвольный отрезок (линейная скорость точки F).

Для колес 2 и 3 точка С – МЦС.

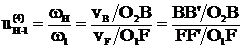
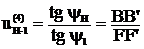
Аналитический способ.

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4

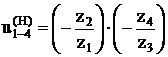
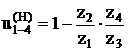
Минусовой механизм.

§5.3 Синтез (проектирование) планетарных механизмов.

Под синтезом в этом курсе будем понимать подбор (определение) чисел зубьев планетарных механизмов при условии, что зубчатые колеса нулевые, а радиальный габарит механизма минимальный.

Расчет на прочность не проводим, но он обязательно должен быть проведен при проектировании.

При проектировании конструктор обязан выполнить ряд условий:

1. Отклонение от заданного передаточного отношения не должно превышать 10% (5%).

2. Обеспечить отсутствие подреза у нулевых зубчатых колес:

У колес с внешними зубьями z₁, z₂, z₃ ≥18 ;

У колес с внутренними зубьями z ≥85.

Если колеса не нулевые, то z_min до 7 илидо 56.

3. Обеспечить отсутствие заклинивания в зацеплении сателлит – коронная шестерня.

Заклинивания нет, если z_кш – z_сат ≥ 8

4. Обеспечить выполнение условия соосности входного и выходного звеньев.

5. Необходимо обеспечить выполнение условие соседства (окружности вершин соседних сателлитов не должны касаться друг друга).

6. Обеспечить выполнение условия сборки. Определить условие сборки, исходя из чертежа невозможно, необходимо проверить выполнение этого условия по уравнению (см. далее).

5.3.1 Проектирование однорядного планетарного механизма.

Дано:

u⁽⁴⁾_1–Н = 6

m = 1 мм

k = 3 – количество сателлитов

Определить:

z₁, z₂, z₃ – ?

при минимальном радиальном габарите;

колеса – нулевые.

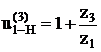à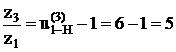

Зададимся числом зубьев z₁ так, чтобы выполнялось условие 2, тогда z₁ = 18, z₃ = 5 ^. 18 = 90 ≥ 85.

Условие соосности записывается в виде

О₁В = О₂В

r₁ + r₂ = r₃ – r₂

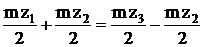
z₁ + z₂ = z₃ – z₂

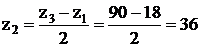
Лекция 12.

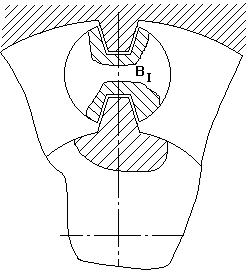
Получим условие соседства.

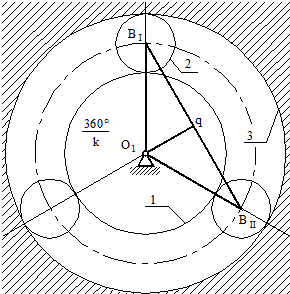Условие соседства: окружности вершин соседних сателлитов не касаются друг друга

В_IB_II > 2 r_a2 (1)

Рассмотрим треугольник O₁B_Iq :

B_IB_II = 2B_Iq

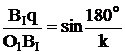
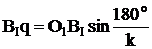
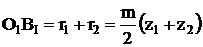
2B_Iq = B_IB_II = m(z₁ + z₂) (2)

r_a2 = r₂ + xm + h_a*m – ∆ym

Т.к. колеса нулевые, то xm = 0 и ∆ym = 0

r_a2 = r₂ + h_a*m

r_a2= 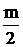(z₂+2h_a*)

2r_a2 = m(z₂ + 2h_a*) (3)

Подставим (3), (2) в (1)

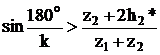(4)

Уравнение соседства справедливо для всех схем, только для схем 2, 3 и 4 в знаменателе стоит правая или левая часть условия соосности, а в числителе вместо z₂ ставят число зубьев наибольшего из сателлитов.

Условие сборки:

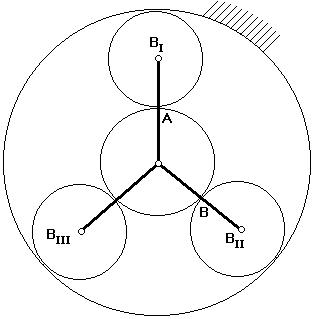Будем считать, что каждый последующий блок сателлитов устанавливается в позиции В_I.

Чтобы освободить место, нужно повернуть водило на угол (360^о / k).

При установке 1–го сателлита зубья центральных колес ориентированы относительно оси симметрии.

Если на дуге АВ укладывается целое число шагов, то при повороте водила на угол (360^о/k) зубья центральных колес будут ориентированы относительно оси симметрии точно так же, как и при установке первого сателлита.

Если на указанной дуге не укладывается целое число шагов, то при повороте водила на угол (360^о / k) зуб 1–го колеса не встанет на то же место и тогда, чтобы установить следующий сателлит, нужно от позиции В_II сделать р дополнительных оборотов водила, чтобы за счет выборки углового шага правильно ориентировать зубья центральных колес.

Уравнение сборки имеет вид:

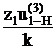= (1 + kp) = γ ,где γ – целое число.

Для нашего случая: 18^.6 (1+ 3р) / 3 = 36 (1+3р)

Условие сборки выполняется при р = 0.

После подбора чисел зубьев определяют радиусы делительных окружностей колес:

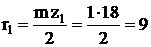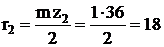мм

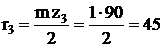мм

мм

По полученным данным строится схема механизма в масштабе и проверяется выполнение передаточного отношения.

5.3.2 Проектирование планетарного механизма со смешанным зацеплением.

Дано:

m=1 мм

Определить:

z1, z2, z3, z4

при условии:

k=3

радиальные габариты – min

колеса – нулевые.

Исходная формула:

u⁽⁴⁾_1–Н = 1 – u^(Н)_1–4= 1 +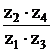

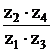= u⁽⁴⁾_1–Н – 1 = 21 – 1 = 20

Представим число (20/1) в виде произведений сомножителей:

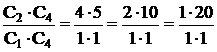
Где С₁~z₁ при этом С₁, С₂, С₃, С₄ – взаимно

С₂~z₂ простые числа, то есть не имеют

С₃~z₃ общих делителей.

С₄~z₄

Указываются все возможные разложения

1: С₁= 4 С₂= 1 С₃= 1 С₄= 5

Запишем условие соосности данного редуктора

О₁В=О₂В

r₁ + r₂ = r₄ – r₃

m ( z₁ + z₂ ) = m ( z₄ – z₃ )

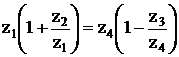
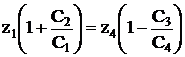
В результате преобразований

z₁ = C₁ ( C₄ – C₃ ) q

z₄ = C₄ ( C₁ + C₂ ) q

где q – коэффициент пропорциональности – любое число но такое, чтобы z было целым.

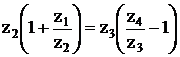
тогда

z₂ = C₂ ( C₄ – C₃ ) q

z₃ = C₃ ( C₁ + C₂ ) q

z₁ = 1 ( 5 – 1 ) q = 4q z₁ = 20

z₂ = 4 ( 5 – 1 ) q = 16q z₂ = 80

z₃ = 1 ( 1 + 4 ) q = 5q z₃ = 25

z₄ = 5 ( 1 + 4 ) q =25q z₄ = 125

q назначается так, чтобы не было подреза, например q = 5.

Проверяем выполнение условия соседства:

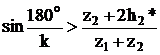
0,87 > 0,82

Условие соседства выполняется.

Проверяем выполнение условия сборки:

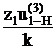= (1 + kp) = γ (a)

20 ^. 21( 1+3p) / 3 = 140 при p = 0

Для передач со сдвоенными сателлитами формула (а) не является общей. Общей формулой является:

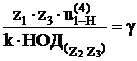
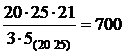– целое

Условие сборки выполняется.

Если хотя бы одно из условий не выполняется, то необходимо рассмотреть следующий вариант разложения на простые множители.

Если, перебрав все возможные варианты разложения, не удалось подобрать числа зубьев, то допускается изменить заданное передаточное отношение в пределах 10 %.

Для других схем числа зубьев подбираются по формулам, представленным в таблице:

	2 внутренних зацепления Схема 3	2 внешних зацепления Схема 4
Условие соосности	z1 – z2 = z4 – z3	z1 + z2 = z4 + z3
z1	C1 ( C4 – C3 ) q	C1 ( C4 + C3 ) q
z2	C2 ( C4 – C3 ) q	C2 ( C4 + C3 ) q
z3	C3 ( C1 – C2 ) q	C3 ( C1 + C2 ) q
z4	C4 ( C1 – C2 ) q	C4 ( C1 + C2 ) q

Глава 6. Кулачковые механизмы.

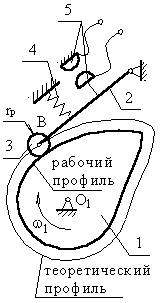
Кулачковым называется механизм, который содержит два основных звена: кулачок и толкатель, образующих высшую кинематическую пару.

Кулачковые механизмы нашли широкое применение в системах газораспределения ДВС, в системах управления электроцепей в вагонах метрополитена (контроллеры).

Достоинства кулачковых механизмов:

1. возможность воспроизведения практически любого закона движения выходного звена;

2. малое количество деталей (кулачок и толкатель), что позволяет просто изготавливать и обслуживать.

Недостаток:

наличие высшей кинематической пары, в которой могут возникать повышенные удельные давления, что может привести к разрушению поверхности кулачка.

Кулачок

Толкатель

Ролик

Пружина

Контакты

Поверхность кулачка, с которой взаимодействует толкатель – рабочий профиль кулачка (действительный).

Поверхность, проходящая через точку В и отстоящая от действительного профиля на расстоянии радиуса ролика – теоретический профиль.

§6.1 Основные схемы кулачковых механизмов.

6.1.1 Кулачковый механизм с поступательно движущимся толкателем.

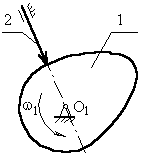а) с центральным толкателем (ось толкателя проходит через ось вращения кулачка);

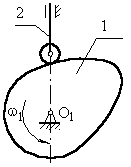
С заостренным

Толкателем

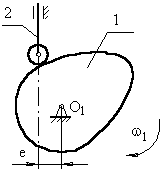б) с внеосным толкателем.

е – эксцентриситет

внеосность левая, т.к. ось толкателя проходит справа оси вращения кулачка.

6.1.2 Кулачковый механизм с поступательно движущимся

толкателем.

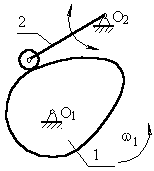
звено 2 (толкатель) совершает возвратно­­–вращающееся движение с центром вращения в точке О₂.

Лекция 13.

§6.2 Основные параметры кулачковых механизмов.

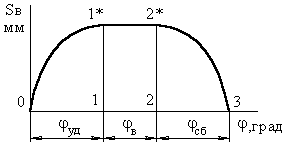
В процессе работы толкатель совершает в соответствии с рисунком 3 движения:

1. поступательно вверх – в этом случае толкатель взаимодействует с участком 01;

2. стоит на месте (выстой) –

контакт с участком 12.

Здесь постоянный радиус кривизны.

3. толкатель опускается (сближение) – контакт с участком 23.

В первой фазе подъему толкателя (фаза удаления) на профиле кулачка соответствует угол ψ_удал;

в фазе выстоя – ψ_выс;

в фазе сближения – ψ_сб.ψ_удал + ψ_выс + ψ_сб = ψ_раб – рабочий угол профиля кулачка.

Угол профилякулачка можно показать только на кулачке.

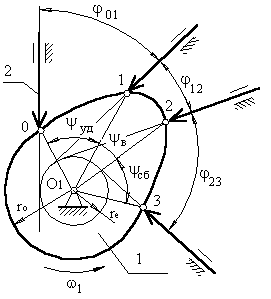Угол поворота кулачка, соответствующий выше указанным фазам перемещения толкателя, определяют, используя метод обращения движения, в соответствии с которым всей системе, включая стойку, мысленно сообщают движение с угловой скоростью (ω₁).Тогда в обращенном движении кулачек становится неподвижным:

ω*₁ = ω₁ + (–ω₁) = 0,

а ось толкателя вместе со стойкой будут перемещаться в направлении (–ω₁). И угол поворота кулачка, соответствующий той или иной фазе движения, определяется по углу поворота оси толкателя в обращенном движении на соответствующем участке. Ось толкателя в обращенном движении в любом положении будет касаться окружности радиуса r_е.

Поворот кулачка на участке :

01 – φ₀₁ 12 – φ₁₂ 23 – φ₂₃

рабочий угол поворота кулачка φ_раб:

φ_раб = φ₀₁ + φ₁₂ + φ₂₃

(уб) (выс) (сб)

Всегда независимо от схемы механизма φ_раб = ψ_раб, а

φ_уд ≠ ψ_уд, φ_выс ≠ ψ_выс, φ_сб ≠ ψ_сб,

для всех схем, кроме кулачкового механизма с центральным толкателем.

§6.3 Построение графика перемещений толкателя при заданном профиле кулачка.

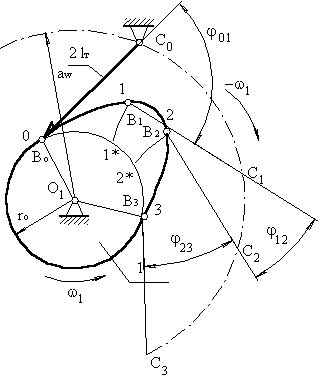Перемещения отсчитываются от начальной окружности радиуса r_o.

Точка В принадлежит толкателю, который повора - чивается вокруг оси С, т.е. т.В перемещается по дуге окружности радиусом r = l_т. Из точки 1 проводим окружность r = l_т до пересечения с окружностью, радиус которой равен расстоянию между тО₁ и тС: r = a_w. Точка пере ­сечения т.С₁ – положение оси вращения толкателя в обращенном движении, когда толкатель контактирует с поверхностью кулачка в

точке 1. Из т.С₁ проводим дугу окружности r = l_т до пресечения с начальной окружностью. Тогда перемещение точки В будет равным длине дуги 11*. На участке 12 толкатель не перемещается. На участке 23 перемещение точки В ищется аналогично перемещению на участке 01.

№
SB,мм

§6.4 Понятие об угле давления.

Угол давления – угол между вектором линейной скорости выходного звена (толкателя) и реакцией, действующей с ведущего звена (кулачка) на выходное звено. Эта реакция без учета сил трения направлена по общей нормали к взаимодействующим поверхностям. Угол давления определяется экспериментально. Для кулачкового механизма с поступательно движущимся толкателем допустимый угол давления равен: [θ] = 25º÷35º.

Для кулачкового механизма с качающимся толкателем допустимый угол давления равен: [θ] = 35º÷40º.

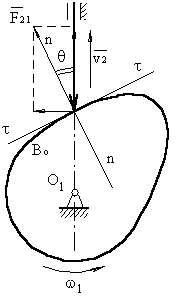
Реакцию можно разложить на две составляющие: 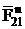и .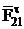

Если, в силу каких‑либо ­­причин, угол давления будет увеличиваться, то 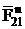будет уменьшаться, а 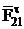– увеличиваться.

При достижении углов больше допустимого, возможен перекос оси толкателя в направляющей.

6.4.1 Вывод формулы для определения угла давления в кулачковом механизме.

Из треугольника ΔКВР:

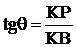(1)

КР = О₁Р – О₁К = О₁ – е

КВ = s_o + s_B

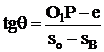(2)

Треугольник ΔО₁ВР подобен треугольнику ΔАВС. Тогда

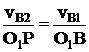­ à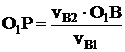

v_B1= ω₁·O₁B

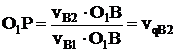
Подставим это выражение в (2):

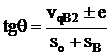
Знак “ – ” – для правой внеосности;

знак “ + ” – для левой внеосности.

Угол давления в кулачковом механизме зависит от размеров кулачковой шайбы: чем она больше, тем угол давления меньше.

6.4.2 Понятие об отрезке кинематических отношений.

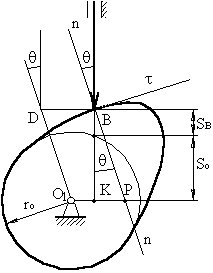
Если из точки В для какого­­‑то текущего положения толкателя проведем линию, параллельную О₁Р, а из центра – || nn, то при их пересечении получим точку D:

BD = O₁P = v_B2 / v_B1 =v_qB2

Из рисунка следует, что перемещение точки В толкателя и, найдя максимальный отрезок кинематического отношения, можно определить положение центра вращения кулачка, отложив внешним образом от точки D допустимый угол давления.

Лекция 14.

§6.5 Синтез (проектирование) кулачковых механизмов по заданному закону движения толкателя.

Под синтезом кулачкового механизма будем понимать построение профиля кулачка, в каждой точке которого угол давления не превышал бы допустимого, а размеры самого профиля были бы минимальны.

Данная задача решается в 3 этапа:

1. Строится график заданного закона движения (как правило либо график ускорения точки В толкателя как функция угла положения – a_B = f(φ₁), либо график линейной скорости точки В – v_B= f(φ₁)). Требуется построить график перемещения точки В как функцию от угла поворота кулачка s_B= f(φ₁).

2. Определение минимального размера кулачковой шайбы при условии, что угол давления в любой точке профиля не превышает допустимого.

3. Построение профиля кулачка.

6.5.1 Построение закона движения оси толкателя.

Дано: Надо построить:

вид графика a_B = f(φ₁), 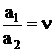графики a_B = f(φ₁)

максимальный ход v_B= f(φ₁)

толкателя h_т s_B= f(φ₁)

b – база графика (сколько отводиться на график по оси φ_1­).

Порядок построения:

1. Произвольно выбирается база графика.

2. Считаем масштаб по оси φ₁:

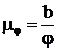, мм/град

3. Если задан симметричный вид графика, то:

φ_уд = φ_сб à b_уд = b_сб

В общем случае закон движения может быть несимметричным.

4. Зададимся произвольным образом а₁= 40 ÷ 50 мм. Тогда

а₂= а₁/ν

Возникает вопрос: каким должно быть расстояние х ?

Его находят из условия равенства площадей под и над осью φ₁.

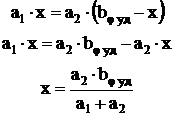
Почему надо выдерживать равенство площадей?

Физический смысл площади под кривой ускорения на площадке х – скорость толкателя на данном участке.

Физический смысл площади под кривой скорости на участке φ_уд – максимальное удаление (перемещение т.В толкателя). Если площади не будут равновеликими, то толкатель, поднявшись на одну величину, опустится на другую.

Построив график ускорения, строим график скорости методом графического интегрирования, выбрав отрезок интегрирования ОК₁. Интегрируя график скорости (с отрезком интегрирования ОК₂, обычно ОК₁=ОК₂), получаем график перемещения т.В толкателя. Полученную ломаную линию заменяют плавной кривой.

Расчет масштаба:

(уS_В)_max на графике перемещений получается автоматически, и его величина зависит от отрезка ОК₂. Тогда, зная ход толкателя, масштаб перемещения будет:

μ=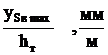

Затем в первом приближении принимаем, что кулачок вращается равномерно, тогда угол поворота кулачка пропорционален времени поворота, и оси φ и t совпадают, но каждая ось имеет свой масштаб.

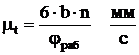
где b – в [мм]; частота вращения кулачка n – [об/мин]; φ_раб – [град].

Масштаб скорости:

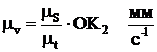
Масштаб ускорения:

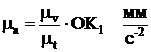
6.5.2 Определение минимального радиуса кулачковой шайбы по известному закону движения толкателя.

6.5.2 а) для кулачка с поступательно движущимся толкателем:

Дано: s_B=f(φ₁); v_B= f(φ₁); [θ]

Определить: r_{o min}

при условии, что угол давления в любой точке профиля кулачка не превышает допустимый.

Порядок построения графика кинематических отношений:

1. проводится вертикальная ось s_B,мм вдоль которой от произвольно выбранной точки В_о (начало отсчета) откладываются отрезки перемещения т.В, взятые с графика s_B=f(φ₁). Масштаб по оси μ_s* перемещений может быть равен масштабу графика перемещений μ_s.

2. 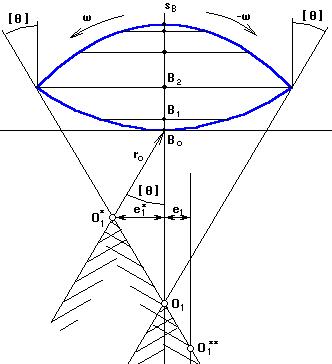в каждой из полученных точек определяют отрезки кинематических отношений, посчитанные в масштабе μ_s*, и откладывают их под углом в 90º по направлению вращения кулачка.

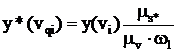мм

Там, где отрезок имеет максимальное значение, восстанавливается перпендикуляр, и под углом [θ] проводится луч.

3. Если учитывать реверс, то второй луч проводят под углом [θ] через отрезок кинематических отношений, отложенный под углом в 90º по направлению реверса и имеющий максимальное значение.

Если реверс не учитывать, второй луч проводят через т.Во под углом [θ]. Если допускается внеосность, то она будет равна е₁*. Если внеосность равна нулю, то центр кулачка будет в т.О₁:

r_o = O₁B_o

Если внеосность задана в техническом задании, например левая, то проводят пряму