Нахождение законов распределения случайных величин, их числовых характеристик, функций и плотностей распределения

Задача 2.5.1

Известен закон распределения дискретной случайной величины (табл. 7).

Таблица 7 – Закон распределения случайной величины Х

Хi	-1
pi	0,1	0,1	0,1	p4

Необходимо:

а) найти вероятности Р(Х = 6), Р(0 < X < 5), P(X ≤ 0);

б) вычислить математическое ожидание и дисперсию случайной величины Х;

в) построить график функции распределения.

Решение:

а) Т.к. все события Х = х_i (i =1, 2, 3, 4) образуют полную группу, будет выполняться:

.

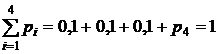Тогда получим: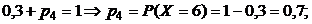

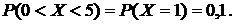
Так как события 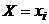несовместны 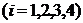, то

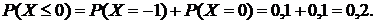
б) Математическое ожидание случайной величины Х находят по формуле (31):

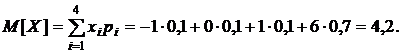
По свойствам дисперсии (35) 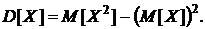При этом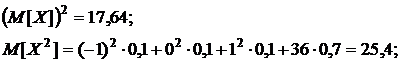

тогда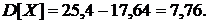

в) Построим график функции распределения случайной величины Х. Значения F(x) можно найти, согласно формуле (24). В таблице 8 представлены значения функции распределения F(x), найденные по условию данной задачи.

Таблица 8 - Значения функции распределения случайной величины Х

Значения
х	F(x) = P(X < x)
x ≤ -1	F(x) = P(X < -1) = 0
-1 < x ≤ 0	F(x) = P(X = -1) = 0,1
0 < x ≤ 1	F(x) = P(X = -1) + P(X = 0) = 0,1 + 0,1 = 0, 2
1 < x ≤ 6	F(x) = P(X = -1) + P(X = 0) + P(X = 1) = 0,1 + 0,1 + 0,1 = 0, 3
x > 6	F(x) = P(X = -1) + P(X = 0) + P(X = 1) + P(X = 6) = 0,1 + 0,1 + 0,1 + 0,7 = 1

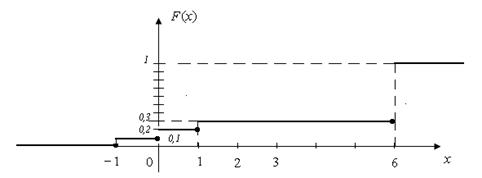
Рисунок 2 – График F(x) к задаче 2.5.1.

Ответ:

а) Р(Х = 6)=0,7; Р(0 < X < 5)= 0,1; P(X ≤ 0) = 0,2;

б) М[Х] = 4,2; D[X]= 7,76;

в) график функции распределения случайной величины Х представлен на рисунке 2.

Задача 2.5.2

На заводе работают три автоматические линии. В течение рабочей смены первая линия не потребует регулировки с вероятностью 0,9, вторая - с вероятностью 0,8, а третья - с вероятностью 0,75. Составить закон распределения числа линий, которые в течение смены потребуют регулировки. Найти среднее квадратическое отклонение этой случайной величины.

Решение:

Случайная величина Х, равная числу линий, которые в течение смены потребуют регулировки, может принимать значения х_i : 0, 1, 2, 3. Все события Х = х_i можно выразить через события А₁, А₂ и А₃. Событие А₁ – первая линия потребовала регулировки, А₂ – вторая и А₃ – третья. По условию,

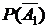= 0,9,

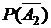= 0,8,

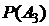= 0,75.

Тогда Р(А₁) = 1- 0,9 = 0,1; Р(А₂) = 1- 0,8 = 0,2; Р(А₃) = 1 - 0,75 = 0,25.

Найдём вероятности событий:

1) Р(Х=0). Выразим событие Х=0 (ни одна линия не потребовала регулировки) через события А₁, А₂ и А₃. Это событие равно произведению 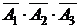. Так как множители в нём – независимые события, то по теореме умножения вероятностей (13) получим:

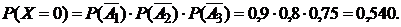
2) Р(Х=1). Событие Х=1 (одна линия потребовала регулировки) можно представить в виде: 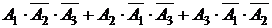. Так как слагаемые в получившейся сумме – несовместные события, а множители в произведениях – независимы, то по основным теоремам теории вероятностей (10) и (13) получим:

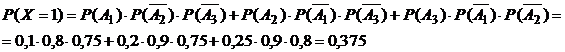
3) Р(Х=2). Событие Х=2 (две линии потребовали регулировки) можно представить в виде: 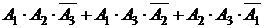. Аналогично пункту 2), получим:

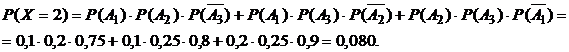
4) Р(Х = 3). Событие Х = 3 (все линии потребовали регулировки) представим в виде: 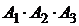. Так как множители – независимые события, то по теореме умножения вероятностей (13) получим:

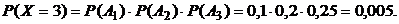
Закон распределения случайной величины Х запишем в виде таблицы (табл. 9).

Таблица 9 - Закон распределения случайной величины Х (к задаче 2.5.2)

Хi
pi = P(X=xi)	0,540	0,375	0,080	0,005

Проверка:

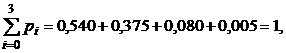(выполняется, т.к. все события X = x_i (i=0, 1, 2, 3) образуют полную группу).

Найдём (по формуле (36)) среднее квадратическое отклонение случайной величины Х: .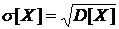

Используя свойство дисперсии (35), вычислим:

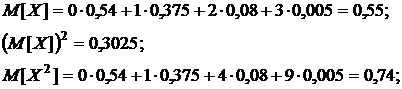
тогда 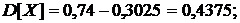следовательно,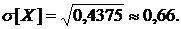

Получили, что в среднем значения случайной величины Х отклоняются от математического ожидания на 0,66.

Ответ:

1) закон распределения случайной величины Х представлен таблицей 9.

2) среднее квадратическое отклонение случайной величины, равной числу линий, которые в течение смены потребуют регулировки, .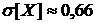

Задача 2.5.3

Плотность вероятности случайной величины Х имеет вид:

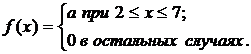
Требуется

а) найти параметр а;

б) вычислить математическое ожидание М[X];

в) найти вероятность Р(1 ≤ Х < 5);

г) построить график функции распределения и плотности вероятности случайной величины Х.

Решение:

а) Из условия следует, что случайная величина Х распределена равномерно, поэтому по свойствам равномерного распределения (26) получим:

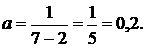
То же значение можно получить по свойствам функции плотности вероятности (25):

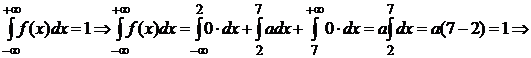
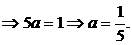
Тогда плотность вероятности случайной величины Х примет вид:

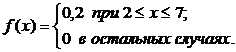
б) Так как математическое ожидание непрерывной случайной величины можно найти по формуле (32), получим:

.

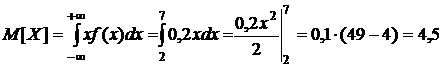в) Для непрерывной случайной величины так же выполняется: Р(Х = х_i) = 0, поэтому, по свойствам плотности распределения случайной величины (стр. 15), получим:

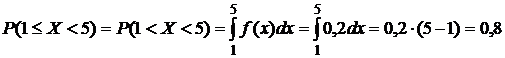
г) Построим графики функции распределения и плотности вероятности случайной величины Х (рис. 3, 4). Значения 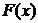найдены в таблице 10.

Таблица 10 - Значения функции распределения случайной величины Х (к задаче 2.5.3).

Значения х	Значения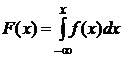
х ≤ 2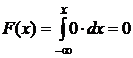
2< х ≤ 7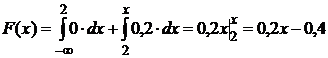
х > 7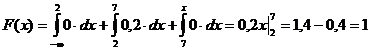

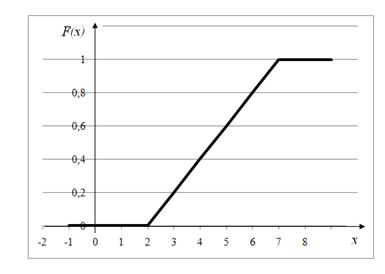
Рисунок 3 - График функции распределения величины Х (к задаче 2.5.3)

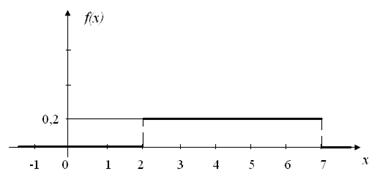
Рисунок 4 - График плотности вероятности

случайной величины Х (к задаче 2.5.3)

Ответ:

а) а = 3; б) М[Х]=4,5; в) Р(1 ≤ Х < 5)=0,8; г) графики функции распределения и плотности вероятности случайной величины Х представлены соответственно на рисунках 3 и 4.