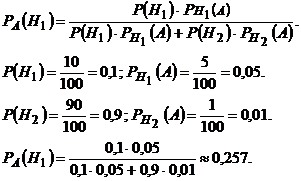Теоремы сложения вероятностей. Теоремы умножения вероятностей. Вероятность появления хотя бы одного события. Формулы полной вероятности и Бейеса

Пример.Стрелок производит два выстрела по мишени. Вероятность попадания при каждом выстреле 0,8. Составить полную группу событий и найти их вероятности.

Решение.

Испытание - Производится два выстрела по мишени.

Событие А - оба раза промахнулся.

Событие В - попал один раз.

Событие С - оба раза попал.

.

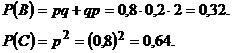
Контроль: P(A) + P(B) + P(C) = 1.

Пример.Согласно прогнозу метеорологов Р(дождь)=0,4; Р(ветер)=0,7; Р(дождь и ветер)=0,2. Какова вероятность того, что будет дождь или ветер?

Решение. По теореме сложения вероятностей и в силу совместности предложенных событий имеем:

Р(дождь или ветер или то и другое)=Р(дождь) +Р(ветер) –Р(дождь и ветер)=0,4+0,7-0,2=0,9.

Пример.На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны?

Решение. Событие А – первый взятый наугад заказ – внутри страны. Событие В – второй тоже предназначен для внутреннего потребления. Нам необходимо найти вероятность 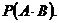Тогда по теореме об умножении вероятностей зависимых событий имеем .

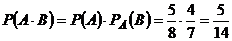Пример.Из партии изделий товаровед наудачу отбирает изделия высшего сорта. Вероятность того, что выбранная вещь окажется высшего сорта равна, 0,8; первого сорта – 0,7; второго сорта – 0,5. Найти вероятность того, что из трех наудачу отобранных изделий будут:

а) только два высшего сорта;

б) все разные.

Решение. Пусть событие 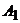- изделие высшего сорта; событие 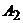- изделие первого сорта; событие 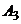- изделие второго сорта.

По условию задачи 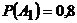; ; 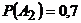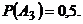События 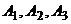- независимы.

а) Событие А – только два изделия высшего сорта будет выглядеть так 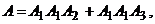тогда

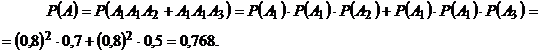
б) Событие В – все три изделия различны - выразим так: 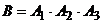, тогда .

Пример.Вероятности попадания в цель при стрельбе из трех орудий таковы: p₁=0,8; p₂=0,7; p₃=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события 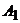(попадание первого орудия), 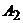(попадание второго орудия) и 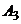(попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям 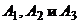(т.е. вероятности промахов), соответственно равны:

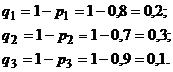
Искомая вероятность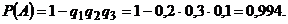

Пример.В типографии имеется 4 печатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События «машина работает» и «машина не работает» (в данный момент) – противоположные, поэтому сумма их вероятностей равна единице: .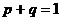

Отсюда вероятность того, что машина в данный момент не работает, равна .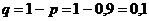

Искомая вероятность .

Пример.Фирма имеет три источника поставки комплектующих – фирмы А,В,С. На долю фирмы А приходится 50 % общего объема поставок, В – 30 % и С – 20 %. Из практики известно, что 10 % поставляемых фирмой А деталей – бракованные, фирмой В – 5 % и С – 6 %. Найти вероятность того, что наудачу выбранная деталь будет бракованной.

Решение. Производится испытание – извлекается одна деталь.

Событие А – появилась бракованная деталь.

Гипотеза Н₁ – деталь фирмы А.

Гипотеза Н₂ – деталь фирмы В.

Гипотеза Н₃ – деталь фирмы С.

Тогда, согласно формуле полной вероятности, искомая вероятность равна:

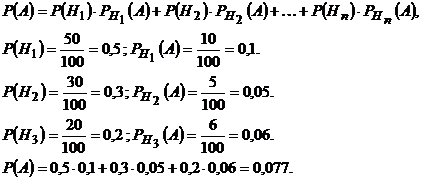
Пример.В центральную бухгалтерию корпорации поступили пачки накладных для проверки и обработки. 90 % пачек были признаны удовлетворительными: они содержали только 1 % неправильно заполненных накладных. Остальные 10 % пачек были признаны неудовлетворительными, так как содержали 5 % неверно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неверно. Учитывая это, какова вероятность того, что вся пачка накладных будет признана несоответствующей стандарту?

Решение. Испытание – проверяется пачка накладных.

Событие А – взятая наугад накладная оказалась неверной.

Гипотеза Н₁ – пачка не соответствует стандарту.

Гипотеза Н₂ – пачка соответствует стандарту.

Необходимо узнать вероятность гипотезы Н₁ при условии, что событие А произошло. Согласно формуле Бейеса имеем: