Расчет цилиндрических передач на выносливость по контактным напряжениям

Основным критерием работоспособности закрытых передач является контактная прочность рабочих поверхностей зубьев. Поэтому основные размеры этих передач определяются из проектного расчета по контактным напряжениям. Цель расчета: предупредить выкрошивание рабочих поверхностей зубьев. При расчете контактных напряжений рассматривают соприкосновение зубьев в полюсе, где происходит их зацепление. Напряжения в высшей кинематической паре распределены по эллиптическому закону аналогично контакту двух цилиндров радиусами r₁и r₂(рисунок 3.27).

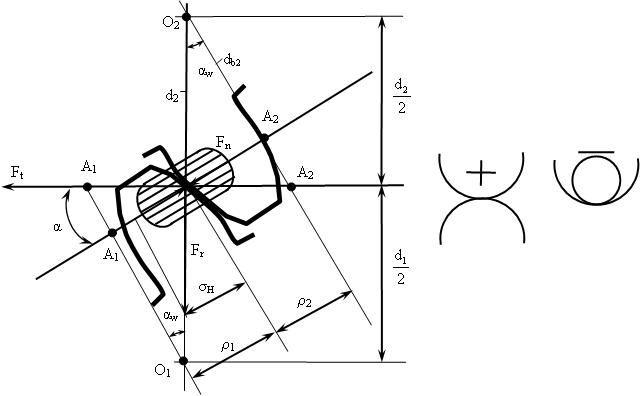
Рисунок 3.27

Максимальные контактные напряжения 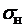для цилиндрических поверхностей определяются по формуле Герца-Беляева:

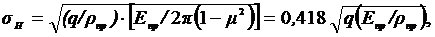
где m = 0,3 - коэффициент Пуассона для стали.

q = (F_n/l_К) К_Н- интенсивность нормальной силы (удельная нагрузка на единицу длины).

Сила нормального давления: F_n= F_t/cos a.

L_К- суммарная длина контактных линий; l_К= b₂ × К_ε × e_α ,

b₂ - длина зуба; К_ε - коэффициент, учитывающий форму сопряженных поверхностей; e_α - коэффициент торцевого перекрытия.

Е_пр= (2E₁× E₂)/(E₁+ E₂) - приведенный модуль упругости, учитывающий материал обоих колес.

r_пр= (r₁× r₂)/(r₁± r₂) - приведенный радиус кривизны. Подставив в формулу Герца выражение, определяющее интенсивность нормальной силы, а также коэффициенты, учитывающие форму сопряженных поверхностей зубьев, коэффициенты, учитывающие механические свойства материала и суммарную длину контактных линий для стальных цилиндрических зубчатых колес, получим формулу проверочного расчета передач на выносливость по контактным напряжениям:

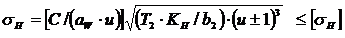
где С = 310 - для прямозубых колес, и С = 270 для косозубых колес.

К_Н- коэффициент нагрузки, учитывающий реальные условия работы колес: К_Н= К_Нa× К_Нb× К_Нv;

К_Нa- коэффициент, учитывающий неравномерность распределения нагрузки между зубьями, зависит от точности изготовления; для прямозубых колес К_Нa= 1, для косозубых выбирают по таблицам;

К_Нb- коэффициент неравномерности нагрузки по ширине колеса, зависит от прогиба валов и перекоса зубчатых колес;

К_Нb= 1,05 - 2,5 из таблиц или графиков;

К_Нv- коэффициент динамической нагрузки, выбирают из таблицы 4.14 в зависимости от окружной скорости, точности изготовления и твердости колес: К_Нv= 1,02 ¸ 1,32.

Для предварительных расчетов принимают К_Н= 1,2...1,5.

Величина расчетных контактных напряжений одинакова для шестерни и колеса. Расчет выполняется для того из колес, у которого меньше допускаемое напряжение [s]_Н(в большинстве случаев для колеса)

[s]_Н2= (s_{Нlim b2}/S_Н) × K_НL,

K_НL- коэффициент долговечности = 1 для общего редукторостроения;

S_Н- коэффициент безопасности = 1,1...1,2;

s_{Н lim b2}= 2 НВ₂ + 70 - предел контактной выносливости при базовом числе циклов.

При проектном расчете необходимо определить межосевое расстояние a_w. Исключим из формулы линейный параметр b .

Обозначим b/a_w= y_ba- коэффициент ширины колеса относительно межосевого расстояния, для редукторов y_ba= 0,2...0,4, тогда b = a_wy_ba, возведем в квадрат вышеприведенное неравенство

[C/(a_w× u)]² (T₂× K_Н/a_w× y_ba) (u ± 1)³ £ [ s_Н]²,

отсюда межосевое расстояние a_w равно:

_{3 ­}______________________

a_w³ (u ± 1) Ö[C/(u × [s]_Н)]²(T₂× K_Н/y_ba), мм

-­ формула для проектного расчета цилиндрических передач на выносливость по контактным напряжениям. Величина a_wуточняется по ГОСТ 2185. Знак «+» для внешнего зацепления, «-» для внутреннего.

Основной параметр m_n - для зубчатых колес выбирается:

m_n = (0,01...0,02) × a_w, мм и уточняется по ГОСТ 9563, для редукторов

m ³ 2...1,5 мм.

Суммарное число зубьев колес: z_S= 2 a_w. соs b/m_n;

число зубьев шестерни: z₁= z_S/(u + 1),

число зубьев колеса: z₂= z_S- z₁; z_S< 200.

3.6.7 Расчет цилиндрических передач на выносливость по напряжениям изгиба

Если расчет зубчатых закрытых передач на контактную прочность выполняется как проектный, то расчет на выносливость зубьев по напряжениям изгиба выполняется как проверочный. Для открытых зубчатых передач расчет зубьев на изгиб является основным. Цель - предотвращение усталостных поломок зубьев.

1) Примем, что в зацеплении находится одна пара зубьев.

2) Сила нормального давления приложена к вершине зуба.

3) Силами трения пренебрегают, т.к. они малы. В этом случае зуб можно представить как балку, защемленную по дуге АВ впадины зуба. От силы F_tволокна в точке В растягиваются. В точке А - сжимаются.

От силы F_r- волокна во всех точках сжимаются (рисунок 3.28).

Усталостные трещины возникают на растянутой стороне - у точки В. Зубья рассчитываются по результирующему напряжению s_F, возникающему на рабочей грани зуба, и равному разности между изгибающим и сжимающим напряжениями:

s_F= s_из- s_сж£ [s_F].

Напряжения изгиба:

s_из= М_из/W = (F_t× h)/W = (2T₂/d₂) × (6/bS²),

где F_t= 2T₂/d_w2; W =bS²/6.

Напряжения сжатия можно не учитывать, s_cж< s_из.

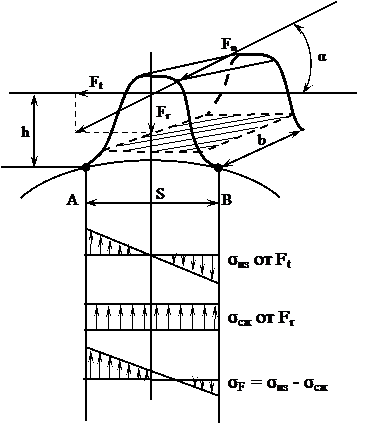
Рисунок 3.28

Тогда результирующее напряжение:

s_F= s_из= (2T₂h 6 K_F)/(d _w2b S²) £ [ s_F].

s_{Flim b}= (1,7 ¸ 1,8)НВ₂; [s_F] = (s_{Flim b}/S_F) K_FL× K_FC,

где К_FL= 1, К_FC= 1, S_F= 1,7 ¸ 1,8;

S_F- коэффициент безопасности;

К_F- коэффициент нагрузки, учитывающий реальные условия работы колес. По аналогии с расчетом на контактную прочность

К_F= К_Fa× К_Fb× К_Fv.

Размеры и форма зубьев зависят от модуля и числа зубьев. Размерные величины h и S неудобны для расчетов. Их удобнее выразить через безразмерные коэффициенты и модуль:

h = h'× m_n; S = S'× m_n;

s_F= (2T₂K_F6h' m_n)/[d_w2b(S'm_n)²] = [2T₂K_F/d_w2b₂m_n] Y_F£ [ s_F];

;

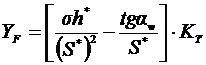K_T – теорет. коэффициент концентрации напряжений;

Y_F= 6h'/(S')²- коэффициент формы зуба.

Учитывая, что d_w2= m × z₂ получается:

для прямозубых колес s_F= [(2T₂K_F)/(z₂b₂m²_n)] Y_F£ [s_F];

для косозубых колес s_F= [(2T₂K_F)/(z₂b₂ m²_n)] Y_F× Y_b£ [s_F].

Формулы для проверочного расчета зубчатых передач.

Величина коэффициента формы зуба Y_Fвыбирается из таблицы в зависимости от числа зубьев прямозубого зубчатого колеса или по эквивалентному числу зубьев z_v= z /cos³b для косозубых и шевронных колес.

Y_b- коэффициент, учитывающий наклон зубьев: Y_b» cos b .

При проектном расчете открытых передач на прочность определяется модуль передачи, т.к. модуль является основным параметром, определяющим размеры зуба и, следовательно, его прочность.

Примем y_bm= b/m_n - коэффициент ширины зуба по модулю.

Для открытых передач y_bm= 6...10 (для прямозубых).

Тогда для прямозубых колес:

[(2T₂K_F)/(z₂y_bmm³_n)] Y_F£ [s_F],

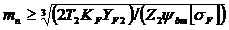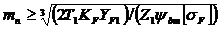откуда или , мм

- формулы для проектного расчета открытых зубчатых передач.

При определении модуля сначала определяют отношение

[s_F1]/Y_F1и [s_F2]/Y_F2и меньшее из значений подставляют в формулу. Полученный расчетный модуль округляют до стандартного.

Число зубьев фактически выбирается в пределах:

z₁= 20...24 - тихоходные передачи, z₁= 26...30 - быстроходные.

z₂= z₁× u. Модуль m_n ³ 2...3 мм.

В открытых передачах зубья изнашиваются более интенсивно, чем в закрытых. Поэтому в формулы вводится коэффициент износа

g = 1,25...1,5, тогда

₃ _____________________

m _n ³ Ö(2T K_Fg Y_F)/(z y_bm [s_F]) , мм.

3.7 Конические зубчатые передачи

Применяются для передачи движения между валами с пересекающимися осями. Угол пересечения осей может изменяться от 10^o< S < 170^o. Конические колеса дороже в изготовлении и сложнее в монтаже. Несмотря на это, имеют широкое применение.

3.7.1 Геометрия конических зубчатых колес

При построении проводим оси 1 и 2 валов. Строим d₁ и d₂ – углы наклона образующих I и II конусов. Длина образующей ограничивается так называемым внешним конусным расстоянием (рисунок 3.29)

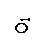
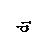
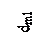
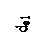
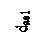
Рисунок 3.29

_________ _______

ОЕ = R_e= 0,5 Öd_e1²+d_e2²= 0,5 m_te× Öz₁²+z₂²,

где m_te- внешний окружной модуль, являющийся стандартным. Конусы ОЕЕ₁и ОЕ₁Е₂- называются основными или начальными конусами.

При вращении зубчатых колес эти конусы перекатываются друг по другу без скольжения аналогично начальным окружностям цилиндрических зубчатых колес.

От точки Е отложим точку С, отношение

b/R_e= y_bRe

- называется коэффициентом ширины зуба по конусному расстоянию. По ГОСТ 12289 y_bRe= 0,285, тогда b = 0,285R_e. Из точек Е и Е₁опустим перпендикуляры к образующим до пересечения с осями валов и получим новые конусы ЕЕ₁О₂и Е₁Е₂О₁.

Конус О₂ЕЕ₁называется наружным дополнительным конусом. Он строится таким образом, что его образующие перпендикулярны образующим основного конуса, основание совпадает с основанием основного конуса, а вершина лежит на оси вращения. Размеры, относящиеся к внешнему торцевому сечению, сопровождают индексом «е» - R_e; d_e:

R_e= R_m+ 0,5b.

Продолжим образующую О₂Е и отложим значение внешнего окружного модуля m_te, т.е. получим высоту головки зуба - точку К.

h_ae= m_te,

Так же на продолжении О₂Е₁получим точку К₁, точки К и К₁соединим с точкой О. ОК и ОК₁- называются образующими конуса выступов. Отложим по ЕО₂отрезок ЕК₂= 1,25 m_teи на Е₁О₂отрезок Е₁К₃= h_fe=1,25 m_te.

ОК₂и ОК₃- называются образующими конуса впадин. Соединим точки С и С₁с точкой О₃. Получим О₃С₁С - внутренний дополнительный конус.

В результате построения получим зуб конического колеса, который ограничивается по длине образующими наружного и внутреннего дополнительных конусов, по высоте - образующими конуса выступов и конуса впадин.

Дополнительные конусы ЕЕ₁О₂и Е₁Е₂О₁характеризуются тем, что в плоскости их образующей зубья перекатываются без скольжения и имеют стандартный параметр. Т.к. зубья конических колес имеют разную высоту по длине, то проектирование их ведется по одному заранее обусловленному показателю.

У прямозубых конических колес это размер на внешнем (большем) торце, где удобнее производить измерения. У непрямозубых - в средней точке, точке М.

Передаточное число:

u = n₁/n₂= z₂/z₁= d_e2/d_e1= tg d₂= ctg d₁,

где d₁и d₂- половины углов при вершинах начальных конусов.

Диаметры окружностей внешних начальных конусов:

d_e1= m_te× z₁; d_e2= m_te× z₂;

Диаметры окружностей конусов выступов:

d_ae1= d_e1+ 2h_ae1× cos d₁; d_ae2= d_e2+ 2h_ae2× cos d₂.

Диаметры окружности конусов впадин:

d_fe1= d_e1- 2h_fe1× cos d₁; d_fe2= d_e2- 2h_fe2× cos d₂.

Средние диаметры:

d_m1= 2 (R_e- 0,5 b) sin d₁; d_m2= 2(R_e- 0,5b) sin d₂.

Понятие о приведенном (эквивалентном) зубчатом колесе (рисунок 3.30).

Действительные профили зубьев конических колес весьма близки к профилям зубьев воображаемых приведенных цилиндрических колес с радиусами начальных окружностей, равным длинам образующих дополнительных конусов.

d_e1= ЕЕ₁; d_m1= MM₁; d_f1= CC₁; d_v1= 2MO₃; d_v1= d_m1/cos d₁.

d_v1- диаметр приведенного (эквивалентного) колеса.

Определим диаметр окружности среднего конуса через d_e1

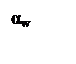
Рисунок 3.30

d_m1/d_e1= (R_e- b/2)/R_e; d_m1= (1 - 0,5 b/R_e) d_e1.

Так как b/R_e= y_bRe, d_m1= (1 - 0,5 y_bRe) d_e1.

Модуль в среднем сечении

m_tm= d_m1/z₁= (1 - 0,5 y_bRe)×d_e1/z₁= (1 - 0,5 y_bRe) m_te.

Параметры приведенного колеса

d_v1= d_m1/cos d₁; z_v1=z₁/cos d₁; z_v2= z₂/cos d₂.

3.7.2 Силы, действующие в зацеплении

В зацеплении действуют три силы (рисунок 3.31):

Окружные силы F_t1= F_t2= 2T₁/d_m1= 2T₂/d_m2.

Сила нормального давления F_n1= F_n2= F_t/cos a.

Радиальная сила приведенного колеса F_rv1= F_rv2= F_t× tg a. Радиальная

сила первого колеса уравновешивается осевой силой второго колеса

F_r1= F_a2= F_rv1× cos d₁= F_ttg a × cos d₁.

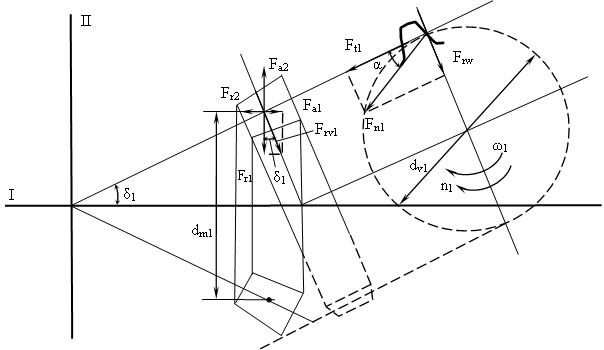Рисунок 3.31

Осевая сила первого колеса уравновешивается радиальной силой второго колеса F_a1= F_r2= F_rv1× sin d₁= F_ttg a × sin d₁.

3.7.3 Особенности расчета конических передач на выносливость по контактным напряжениям

Цель расчета: предупредить выкрошивание рабочих поверхностей зубьев. Исходная формула Герца-Беляева

___________________

s_Н= Ö(q/r_пр) [E_пр/2 p(1 - m²)] £ 0,85 [s_Н].

Учитывая консольное расположение колес, допускаемые контактные напряжения принимают на 15% меньше.

Для закрытых передач расчет выполняется для колеса как проектный, то есть определяется d_e2- диаметр окружности внешнего начального конуса колеса.

q = (F_n/l_К) К_Н- интенсивность нормальной силы (удельная нагрузка на единицу длины).

Сила нормального давления

F_n= F_t2/cos a = 2T₂/d_m2cos a = 2T₂/[d_e2(1 - 0,5 y_bRe) cos a].

К_Н= К_Нa× К_Нb× К_Нv- коэффициент нагрузки, учитывающий реальные условия работы (аналогично цилиндрическим передачам).

y_bRe= b/R_e- коэффициент длины зуба по конусному расстоянию = 0,285;

l_К- длина контактных линий; l_К= b × К_Σ× e_a;

К_Σ- коэффициент, учитывающий суммарную длину контактных линий;

e_a- коэффициент торцевого перекрытия для косозубых колес.

Итак, q = (2T₂K_н)/[b d_e2(1 - 0,5 y_bRe) cos a × K_Σ× e_a];

Е_пр= 2E₁E₂/(E₁+ E₂) - приведенный модуль упругости, учитывающий материал обоих колес,

при Е₁= E₂; Е_пр= Е₁= Е₂; для стали Е = 2,15 × 10⁵Н/мм².

r_пр= (r₁× r₂)/(r₁+ r₂) - приведенный радиус кривизны профиля. Подставим в формулу Герца выражение, определяющее интенсивность нормальной силы, а также коэффициенты нагрузки, формы зуба, коэффициент, учитывающий механические свойства материала и коэффициент, учитывающий суммарную длину контактных линий, после преобразования получим при
S = 90^o: _________________

s_Н= [(2.z_Н.z_Е.z_Σ)/ (0,85 (1-0,5y_bRe))] ×Ö(T₂K_Нu)/(d³_е2y_bRe) £ [s_Н],

где z_Н, z_Е, z_Σ- коэффициенты, учитывающие соответственно форму сопряженных поверхностей, механические свойства материалов колес и суммарную длину контактных линий.

Частный вид формулы для стальных зубчатых колес:

Е = 2,15 × 10⁵Н/мм², при a = 20^o;

С = (2. z_Н× z_E× z_Σ)/0,85 = 950.

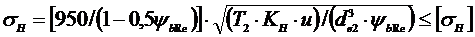- формула для проверочного расчета стальных конических зубчатых колес на выносливость по контактным напряжениям.

При проектном расчете определяется d_е2- диаметр окружности внешнего начального конуса колеса, чтобы освободиться от радикала, возведем в квадрат вышеприведенное неравенство:

[950/(1 - 0,5 y_bRe]²× [(T₂K_Нu)/(d³_е2× y_bRe)] £ [s_Н]².

Откуда: ₃ ________________________________

d_е2³ Ö[950/(1-0,5 y_bRe) [s_Н]]²× (T₂K_Нu) / y_bRe, мм

- формула для проектного расчета конических передач.

Расчетное значение d_е2округляется до ближайшего большего стандартного значения.

3.7.4 Особенности расчета конических передач на выносливость по напряжениям изгиба

Этот расчет выполняется как проверочный, с целью предупредить поломку зубьев.

В плоскости приведенного зубчатого колеса рассмотрим силы, действующие на зуб (рисунок 3.32, а).

В точке М на середине зуба по линии нормального зацепления действует сила нормального давления. Перенесем силу по линии действия на ось симметрии и разложим ее. Опасное сечение представляет собой трапецию (рисунок 3.32, б):

АВ - опасное сечение, оно будет под точкой М в середине зуба. Центр тяжести у трапеции не в середине, а на расстоянии 0,4 b от большего основания, т.к. мы рассчитываем несколько ослабленное сечение (т.е. середину зуба), это компенсируется уменьшением на 15% [s]_F, т.е. принимаем 0,85 [s]_F, и в дальнейшем считаем опасное сечение прямоугольным с шириной S и длиной b. Аналогично цилиндрическим колесам, зубья конического колеса рассчитываются по результирующему напряжению s_Fу основания зуба, равному разности изгибающих и сжимающих напряжений:

s_F= s_из- s_сж£ [ s_F] × 0,85.

Напряжения изгиба:

s_из= М_из/W = (F_th)/W = (2T₂h/d_m2) × (6/bS²),

где F =2T₂/d_m2; W = bS²/6.

Напряжение s_сж<< s_изможно не учитывать s_сж= F'_r2/bS.

s_F= s_из= (2T₂h 6 K_F)/(0,85 d_m2b S²) £ [ s_F],

где K_F= К_Fa× К_Fb× К_Fv- коэффициент нагрузки, учитывающий реальные условия (аналогично цилиндрическим передачам).

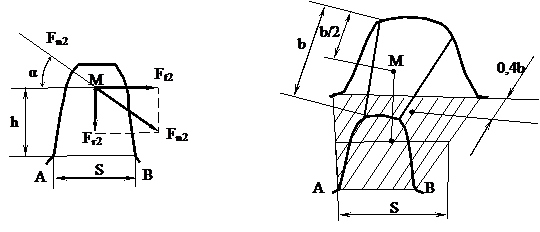
а) б)

Рисунок 3.32

Учитывая, что d_m2= m_tm× z₂, по аналогии с цилиндрическими передачами s_F2= [(2,36 T₂K_Fγ)/(b₂z₂m²_tm)] × Y_F2£ [ s_F] - формула для проверочного расчета конических колес на изгиб, m_tm=(1-0,5y_bRe)m_te, где m_tm- средний модуль; m_te- торцевой модуль.

Коэффициент формы зуба 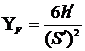выбирается из таблиц в зависимости от приведенного числа зубьев:

z_v1= z₁/cos d₁; z_v2= z₂/cos d₂.

При проектном расчете открытых конических передач определяется модуль в среднем сечении.

В открытых передачах зубья изнашиваются более интенсивно, чем в закрытых, поэтому в формулу вводится коэффициент износа, учитывающий снижение прочности g = 1,25...1,5.

Примем y_bm= b/m_tm= 10...15 - коэффициент длины зуба по модулю в среднем сечении, тогда: s_F2= [(2,36 T₂K_Fγ) /(z₂y_bm×m_tm³)] Y_F£ [s_F],

₃ _________________________

откуда: m_tm³ Ö[(2,36 T₂K_Fγ)/(z₂y_bm[s_F])]×Y_F2, мм.

При определении модуля сначала определяются отношения [s_F]₁/Y_F1 и [s_F]₂ / Y_F2 и меньшее значение подставляется в формулу.

Полученный расчетный модуль округляется до ближайшего большего стандартного.

3.8 Червячные передачи

Применяются для передачи вращающего момента между валами, у которых угол скрещивания осей обычно составляет 90^о(рисунок 3.33).

Червячная передача - это винтовая передача, у которой ведущее звено - червяк имеет от 1 до 4 заходов (витков), а ведомое - червячное колесо ³ 28 зубьев.

а) б)

Рисунок 3.33

Ведущим в червячной передаче является червяк, т.е. короткий винт с трапецеидальной или близкой к ней резьбой.

Если червячное колесо представляет собой цилиндрическое косозубое колесо, то зубья имеют точечный контакт, малую нагрузочную способность и повышенный износ (рисунок 3.33, а).

Наиболее широко распространены колеса с зубьями дугообразной формы, которые охватывают червяк по дуге с углом 2 g = 60...110^о.

При этом возникает линейный контакт, следовательно, повышается нагрузочная способность передачи (рисунок 3.33, б).

Параметрам червяка приписывается индекс - 1.

Параметрам колеса - 2.

Достоинства червячной передачи:

1) плавность и бесшумность работы;

2) компактность;

3) возможность получения больших передаточных чисел (до 1000);

4) возможность получения самотормозящей передачи.

Недостатки:

1) низкий КПД, вследствие скольжения;

2) значительное выделение тепла;

3) применение для венцов червячных колес дорогостоящих антифрикционных материалов;

4) повышенный износ колес.

Применяются червячные передачи при небольших и средних мощностях до 50 кВт, предпочтительно в приводах периодического действия (во избежание перегрева).

3.8.1 Классификация червячных передач

В зависимости от формы внешней поверхности червяка передачи бывают с цилиндрическим или с глобоидным червяком.

Глобоидная передача имеет повышенный КПД, более надежна и долговечна, но из-за сложности изготовления имеет ограниченное применение.

В зависимости от направления винтовой линии резьбы червяка передачи бывают с правым или левым червяком.

Наибольшее применение имеют правые червяки.

В зависимости от числа заходов резьбы червяка передачи бывают с однозаходным или многозаходным червяком.

В зависимости от расположения червяка относительно колеса передачи бывают с нижним, верхним и боковым червяком.

При V_S £ 4 м/с - нижний червяк;

При V_S > 4 м/с - верхний червяк;

где V_S – скорость скольжения.

В зависимости от формы винтовой поверхности резьбы цилиндрического червяка передачи бывают с архимедовым, конволютным и эвольвентным червяком. Каждый из них требует различных способов нарезания.