Кинематический анализ механизмов передач

Заключается в определении угловых скоростей и передаточных отношений.

Аналитический метод

а) Зубчатые цилиндрические передачи (рисунок 3.17).

Имеют наиболее широкое распространение в машиностроении как с внешним, так и с внутренним зацеплением.

W – мгновенный центр вращения в относительном движении колес 1, 2 (полюс зацепления).

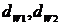- начальные окружности зубчатых колес.

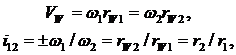
т.к. ,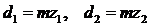

то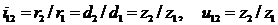

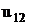- передаточное число, т.е. отношение числа зубьев колеса к числу зубьев шестерни.

По аналогии для других видов передач в дальнейшем будем принимать, что .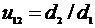

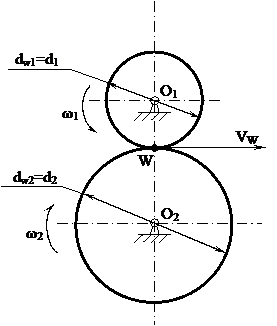
Рисунок 3.17

В рядовом механизме имеем как бы последовательно расположенные отдельные ступени, каждая из которых представляет собой два звена 1-2, 2-3, ... (рисунок 3.18).

Общее передаточное отношение 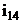равно произведению передаточных отношений отдельных ступеней.

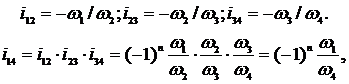
(-1)ⁿ – определяет знак передаточного отношения, где n – число внешних зацеплений.

В нашем случае п=3, (-1)³ = -1, т.е. вращение звена 4 не совпадает с направлением вращения ведущего звена 1.

В рядовых механизмах общее передаточное отношение равно произведению частных.

Общее передаточное число

u₁₄ = u₁₂ u₂₃ u₃₄ = u_общ

или

.

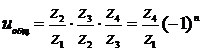Рисунок 3.18

Для данного ряда промежуточные зубчатые колеса не влияют на угловую скорость ведомого (выходного) звена. Промежуточные зубчатые колеса применяются для изменения направления вращения ведомого звена и для передачи движения на средние расстояния.

Ступенчатое расположение зубчатых колес (рисунок 3.19):

I, IV – ведущий и ведомый валы,

II, III – промежуточные валы.

Передаточное отношение для схемы .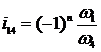

Передаточные числа отдельных ступеней

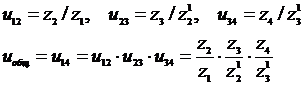
или с учетом направления вращения

,

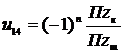где в числителе произведение чисел зубьев колес, в знаменателе – произведение чисел зубьев шестерен.

Рисунок 3.19

Такое соединение позволяет реализовать значительные передаточные числа;

б) Дифференциальные механизмы с внешним (рисунок 3.20, а) и внутренним контактом (рисунок 3.20, б).

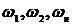- истинные угловые скорости звеньев; Н – водило (HEBEL).

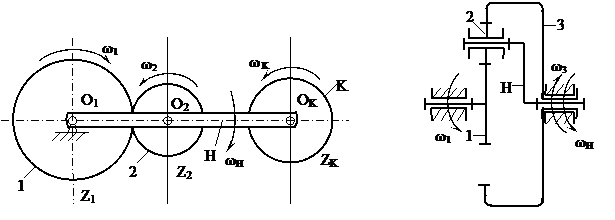
а) б)

Рисунок 3.20

Применим метод обращенного движения. Зададим всем звеньям механизма вращение вокруг оси О₁ с угловой скоростью - 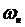, но в обратном направлении.

При этом водило остановится и дифференциальный механизм обращается в рядовой.

Угловые скорости в обращенном движении (при остановленном водиле)

.

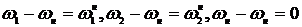Передаточное отношение при остановленном водиле

.

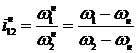Отсюда

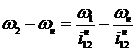
и

.

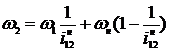В общем случае при числе колес равным К

;

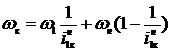в) Планетарный механизм отличается от дифференциального тем, что зубчатое колесо 1 – неподвижно (рисунок 3.21, а).

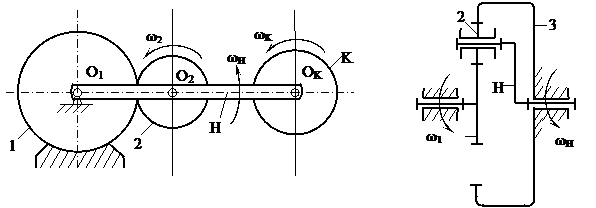
а) б)

Рисунок 3.21

Так как у планетарного 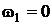, то в общем случае при числе зубчатых колес равным К

.

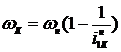В планетарных механизмах с внутренним зацеплением в большинстве случаев неподвижно 3 колесо (z₃) (рисунок 3.21, б).

Формула Виллиса

,

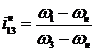при .

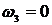
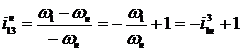Формула Виллиса при торможении 3 колеса

.

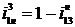Для схемы (рисунок 3.20, б) при остановленном водиле

.

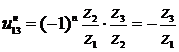Передаточное отношение планетарного редуктора

.

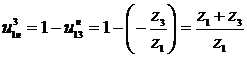Графоаналитический метод

В основе метода лежит построение планов линейных и угловых скоростей звеньев механизмов.

Если звено вращается вокруг центра вращения О₁ (рисунок 3.22), то скорости точек, лежащих на звене, перпендикулярны к этому звену и пропорциональны расстояниям до центра вращения О₁.

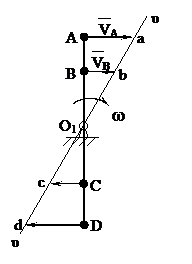
Рисунок 3.22

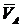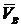Концы векторов и располагаются на прямой, проходящей через центр вращения О₁. Треугольник О₁Аа (О₁Вb) называется картиной линейных скоростей звена, а прямая 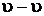- тэта-линия ( 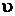- линия).

Имеем кинематическую схему двухступенчатой передачи, для которой известны диаметры начальных окружностей всех колес и угловая скорость 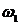ведущего вала 1. Схема механизма построена в масштабе 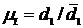м/мм (рисунок 3.23, а).

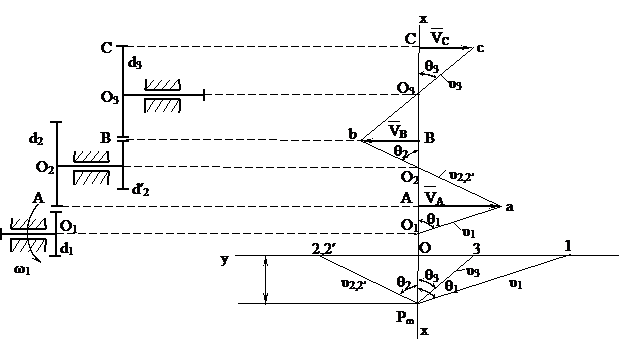
а) б)

Рисунок 3.23

Проводим линию хх, на которую проектируем характерные точки передачи – центры вращения О₁, О₂, О₃ и точки контакта сопряженных колес А и В (рисунок 3.23, б). Для ведущего звена 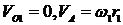. На линии хх от точки А перпендикулярно хх откладываем отрезок 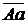, изображающий в выбранном масштабе 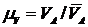(м/с)/мм вектор - 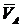мм. Соединяя точки О₁ и а, получаем 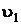- линия звена 1 – геометрическое место концов скоростей всех точек отрезка О₁А.

Поскольку в точке А колеса 1 и 2 имеют одну и ту же линейную скорость V_A, а в точке О₂, скорость блока колес 2 и 2' равна нулю, то соединяя а и О₂, строим линию 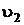- линию для блока колес 2 – 2'.

Продолжая эту линию до пересечения с прямой, проведенной через точку В перпендикулярно хх, получаем отрезок Вb, изображающий в масштабе 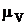линейную скорость точки В колес 2', а следовательно и колеса 3 - .

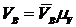Для построения 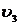- линии достаточно соединить точку b с точкой О₃.

Получили план линейных скоростей передачи, причем 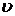- линия неподвижного звена передачи совпадает с прямой хх, .

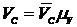Угловые скорости звеньев:

,

,

.

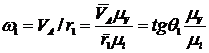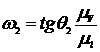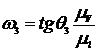Передаточные отношения

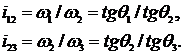
Отношение тангенсов углов 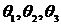можно заменить отношением отрезков. Для этого построим план угловых скоростей (рисунок 3.23, б).

Проводим линию уу, перпендикулярно прямой хх, через произвольную точку 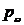(полюс плана угловых скоростей) проводим лучи под углом 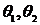и 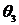(соответствующие 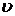- линии). Н – полюсное расстояние, мм.

Отрезок 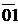в масштабе 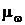изображает угловую скорость колеса 1

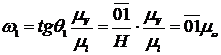
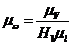, (1/c)/мм – масштабный коэффициент плана угловых скоростей.

Аналогично 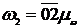; 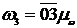искомое передаточное отношение определяется отношением отрезков 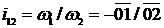причем передаточное отношение имеет знак плюс, если оба отрезка расположены по одну сторону от точки О, и знак минус, если по разные стороны.

Имеем схему планетарной передачи, построенной в масштабе 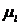(рисунок 3.24, а).

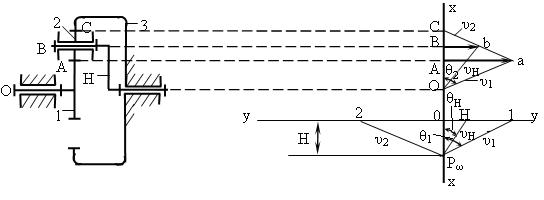
а) б)

Рисунок 3.24

Мгновенный центр относительного вращения сателлита 2 находится в точке С, точке касания его начальной окружности с начальной окружностью неподвижного центрального колеса 3. Построим план линейных скоростей.

На линию хх проектируем точки О, А, В, С. Из точки A отложим отрезок Аа произвольной длины, изображающий в масштабе 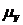скорость V_A (рисунок 3.24, б).

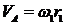, м/с.

Масштабный коэффициент плана линейных скоростей

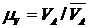, (м/c)/мм.

Соединив точку а с точками О и С, получим треугольник скоростей солнечного колеса 1. Скорость сателлита и водила, определяется графически отрезком Вb. Соединив точку b с точкой О, получим треугольник скоростей водила Н ( 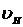- линия водила).

Обозначим соответствующие углы 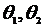и .

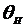Проводим линию уу. Через произвольную точку 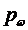проводим лучи под углом 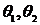и 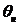(соответствующие 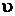- линии).

Отрезок 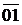в масштабе 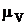изображает угловую скорость колеса 1:

,

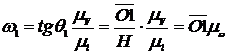где 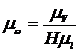(1/с)/мм - масштабный коэффициент плана угловых скоростей.

Аналогично 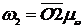; 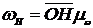искомое передаточное отношение определяется отношением отрезков .

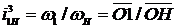Передаточное отношение имеет знак плюс, если оба отрезка расположены по одну сторону от точки О и знак минус, если по разные стороны.

Угловые скорости, найденные графическим методом, следует сравнить со значениями, найденными аналитическим методом

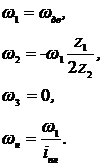
3.6.5 Силы, действующие в зацеплении

Пренебрегают силами трения и считают, что сила нормального давления F_n для прямозубной передачи приложена в полюсе зацепления и направлена по линии зацепления, как общей нормали к рабочим поверхностям зубьев. Эта сила является равнодействующей окружной F_tи радиальной F_rсил (рисунок 3.25).

S М_ox= 0, т.е. F_t1×d₁/2 - T₁= 0,

откуда F_t1= F_t2= 2T₁/d₁= 2T₂/d₂; F_r1= F_r2= F_t× tg a ;

F_n1= F_n2= F_t/cos a.

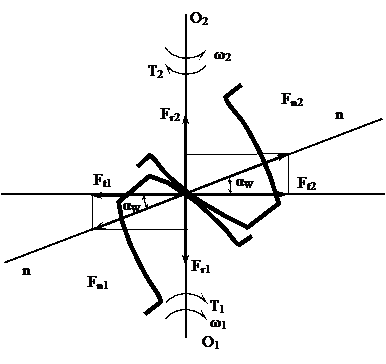
Рисунок 3.25

Рисунок 3.26

Недостатком косозубых колес является наличие осевой силы F_а в зацеплении. Прочность зуба определяют его размеры и форма в нормальном сечении, причем форму косого зуба в нормальном сечении принято определять через параметры приведенного (эквивалентного) прямозубого колеса, диаметр которого: d_v= m_n× z_v, (рисунок 3.26).

z_v= z/cos³b - эквивалентное число зубьев приведенного колеса. Окружная сила приведенного колеса: F_tv= F_t/cos b .

Силы в косозубом зацеплении: F_t1= F_t2= 2T₁/d₁≈ 2T₂/d₂;

F_a1= F_a2= F_t× tg b; F_r1= F_r2= F_tv× tg a = F_t× tg a/cos b;

F_n1= F_n2= F_tv/cos a = F_t/(cos a × cos b).