Устойчивость сжатых стержней

Форма равновесия в деформированном состоянии считается ус­тойчивой, если система при любом малом отклонении от начального состояния равновесия восстанавливает свою форму после снятия внешней нагрузки.

Переход системы из устойчивого состояния в неустойчивое на­зывают потерей устойчивости, а границу этого перехода - критичес­ким состоянием системы.

На рисунке 2.41 показана потеря устойчивости консоли (а) и арки (б) при изгибе.

Рисунок 2.41

При сжатии короткого бруса большой жесткости брус устойчи­вости не теряет (рисунок 2.42, а).

Длинный и тонкий стержень может потерять устойчивость при сжатии (ри­сунок 2.42, б), при этом он будет работать на сжатие и изгиб: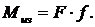

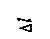
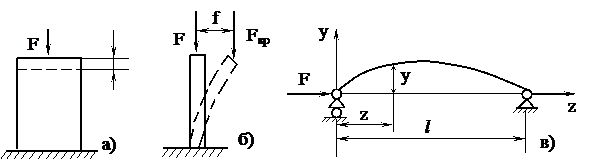
Рисунок 2.42

Та нагрузка, при которой заданная форма равновесия перестает быть устойчивой, называется критической нагрузкой. Критическая нагрузка является столь же опасной, как и разрушающая нагрузка, т.к. потеря устойчивости нередко сопровождается разрушением.

Поэтому при сжатии стержней малой жесткости условие проч­ности должно быть дополнено условием устойчивости:

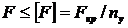- допускаемая нагрузка должна быть меньше крити­ческой; или 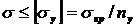- допускаемое напряжение должно быть меньше критического;

n_у - коэффициент запаса устойчивости, учитывающий влияние на проч­ность таких факторов, как начальная кривизна стержня, эксцентриси­тет приложения нагрузки и др.

Потеря устойчивости возможна не только в случае сжатия тонких стерж­ней, но также при изгибе, кручении и сложных видах деформаций.

2.9.1 Формула Эйлера для определения критической силы сжатого стержня

При выводе формулы принимают следующие допущения:

1) В момент потери устойчивости стержень работает упруго, т.е.
после удаления критической силы он вновьвыпрямляется;

2) В момент потери устойчивостиупругие деформации малы,
что позволяет использовать приближенное дифференциальное урав­нение изогнутой оси стержня;

3) Собственным весом стержня можно пренебречь (рисунок
2.42, в). Имеем прямой стержень (рисунок 2.42, в), который под дей­ствием силы изогнулся. Цель расчета: найти силу, которая в состоянии
изогнуть стержень.

Дифференциальное уравнение изогнутой оси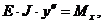

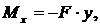
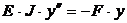
или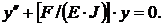

Обозначим F/(E · J) = k², получим:

у" + k²у = 0. (2.25)

Полный интеграл этого уравнения:

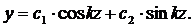(2.26)

Из условия закрепления имеем:

1) При z = 0, y = 0, подставим в (2.26):

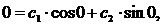откуда: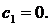

2) При z = l, у = 0, подставим в (2.26):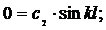

с₂ ≠ 0, иначе у = 0, т.е. стержень бы остался прямым.

Следовательно, sin kl = 0, а это будет при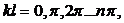

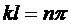, n- любое целое число

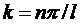или 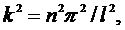но k² = F/(E · J).

Следовательно, 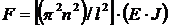- получаем множество кри­тических сил, каждой из которых соответствует своя форма равнове­сия. Так при n = 1 (первая критическая сила) стержень изгибается по одной полуволне синусоиды, а при всех последующих значениях n число полуволн равно номеру соответствующей критической силы.

Тогда, положив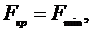

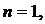
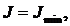
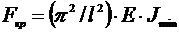- формула Эйлера, для практических целей ин­терес представляет только наименьшая критическая сила.

Величина критической силы для сжатого стержня зависит от упругих свойств материала - Е; формы и размеров сечения - J_min; дли­ны стержня - l; условия закрепления.

Помимо рассмотренного случая шарнирного закрепления обо­их концов стержня, возможны и другие способы закрепления.

В этих случаях пользуются обобщенной формулой Эйлера.

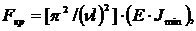
где 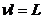- приведенная длина стержня;

v - коэффициент приведения длины, зависящий от условий закрепле­ния стержня (рисунок 2.43).

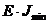- минимальная жесткость стержня. Так для стержня прямоу­гольного сечения: J_x=ab³/12; J_v = ba³/12; .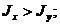

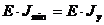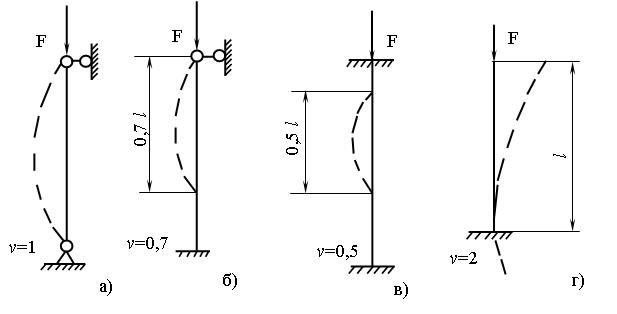
Рисунок 2.43