Определение удельных нагрузок на провода и тросы
Провода и тросы воздушных линий испытывают действие нагрузок – вертикальных (вес провода и гололеда) и горизонтальных (давление ветра). В результате этого в металле возникают растягивающие напряжения.
При расчётах удобно пользоваться удельными (приведёнными) нагрузками, которые относятся к 1 м длины линии и 1 мм2 сечения провода (троса).
Удельные нагрузки рассчитывают исходя из условия, что нагрузка по длине провода в пролёте распределяется равномерно и порывы ветра отсутствуют.
Нагрузка от собственного веса провода вычисляется в зависимости от материала провода и его конструкции
,
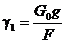где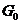 
– масса провода; 
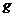– ускорение свободного падения; F – суммарная площадь поперечного сечения всех проволок провода или троса.
Нагрузку от веса гололеда определяют исходя из условия, что гололедные отложения имеют цилиндрическую форму плотностью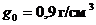 
:
,
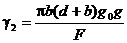где d – диаметр провода;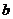 
– толщина стенки гололеда, принимаемая в зависимости от климатического района по гололеду и номинального напряжения линии.
Нагрузка от собственного веса провода и гололеда направлена вертикально и определяется по формуле
.
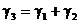Нагрузка от давления ветра при отсутствии гололеда рассчитывается согласно выражению
,
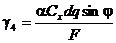где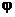 
– угол между направлением ветра и проводами линий, в расчётах принимается равным 90°; q – скоростной напор ветра; 
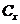– аэродинамический коэффициент, равный 1,1 для проводов и тросов диаметром 20 мм и более, не покрытых гололедом, и 1,2 – для не покрытых гололедом проводов и тросов диаметром менее 20 мм, а также для всех проводов и тросов, покрытых гололедом; 
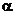– коэффициент, учитывающий неравномерность скорости ветра по длине пролёта, находится в пределах 1,0...0,7.
Нагрузка от давления ветра при наличии гололеда рассчитывается аналогично, но с учетом увеличения площади боковой поверхности провода из-за гололеда
.
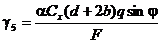Суммарная нагрузка от собственного веса проводов и давления ветра (при отсутствии гололеда) составляет
.
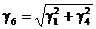Суммарная нагрузка от собственного веса провода, гололеда и давления ветра равна
.
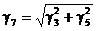При проектировании следует учитывать, что если линия имеет большую длину, то её отдельные участки могут оказаться в неодинаковых климатических условиях. Такое положение наиболее часто возникает при прохождении трассы по горам, мимо широких рек и больших водоемов. Для разных частей такой линии расчётные климатические условия могут приниматься различными.
Следует заметить, что удельные нагрузки определяются и вводятся в расчёты не произвольно, а для определенных технически обоснованных расчётных сочетаний климатических условий (табл. 1).
Данные для расчёта удельных нагрузок приведены в ПУЭ.
Критическая температура
Как следует из формулы (3.16), стрела провеса при неизменной длине пролёта зависит от величины нагрузки γ и напряжения σ, которое, в свою очередь, зависит от нагрузки и температуры. Таким образом, на стрелу провеса влияет нагрузка и температура. В зависимости от отношения γ/σ стрела провеса может получиться большей тогда, когда на провод действует дополнительная нагрузка (гололед, ветер) при относительно низкой температуре либо когда провод находится только под действием своего веса при более высокой температуре. Очевидно, существует и такая температура, при которой провод под действием только своего веса будет иметь такую же стрелу провеса, как в режиме дополнительной нагрузки. Эта температура называется критической. Выведем формулу для её определения.
Пусть провод находится под действием дополнительной нагрузки γг (гололед, ветер) при температуре tг и имеет стрелу провеса fг при напряжении σг. При критической температуре tK нагрузка от собственного веса равна γ1 и стрела провеса fк.
Тогда из условия fк =fг по формуле (3.16) можно записать
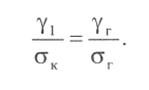
Отсюда напряжение при критической температуре
Критическую температуру получим, подставив σк из формулы (3.32) в уравнение состояния провода (3.23):
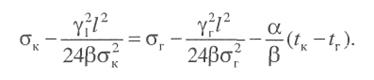
Отсюда
