Е)-проектирование: алгебраические,геометрические

Пусть даны две непараллельные прямые на плоскости, тогда можно спроектировать вектор на прямую вдоль другой прямой

AB = A_xB_x + A_yB_ya = a_x + a_y (1) a_xÎox, a_yÎoya_x, a_y – геом. проекции.

Алгебраическая проекция на ось – координата геом. проекции в базисе этой прямой. пр^┴_ea = |a| cos(a^۸e).

Разложение (1) вектора а на составляющие (геом. проекции) единственно.

Док-во: a = b_x + b_y (1) a = (a_x – b_x) + (a_y – b_y) => a_x = b_x a_y = b_y

a = a_π + a_l(2) Разложение (2)

Пр^l_π a = a_πПр^π_l a = a_l

Алгебраическое проектирование – это проектирование на числовую ось. Каждый вектор приобретает координату – число. Алг. проекция вектора на координатную ось –^def координата геом. проекции этого вектора на ту же ось (в той системе корд., которая на этой оси задана).

Ж)-частный случай проектирования(ортогональность)

Векторы ортогональны, если их скалярное произведение=0.

З)-направляющие углы

i, j, k – ОНБ (ортонормированный базис) ā = a₁i + a₂j + a₃ka≠Ō В ОНБ i, j, k {ā*i = a₁; ā*j = a₂; ā*k = a₃}(2) = {|ā|cos(a۸i) = a₁; |ā|cos(a۸j) = a₂; |ā|cos(a۸k) = a₃} = {a₁ = |ā|cosα; a₂ = |ā|cosβ; a₃ = |ā|cosγ}(3) α = ā^۸i, β = ā^۸j, γ = ā^۸k. Косинусы углов α, β и γ назыв. направляющими косинусами вектора ā.

и)-косинусы векторов

К)-векторное произведение

Векторнымпроизведениемaнаbназываетсявекторc, что:

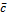| |=| || |sin( ^ )

,

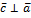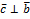
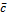, , – правая

Замечание. Определение годится для неколлинеарных векторов aи b.

Л)-свойства векторного произведения

1. [ , ] = 0 ó || (векторы коллинеарны, когда хотя бы один из множителей 0)

2. [ , ] = -[ ]

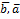3. [ , ] = [ , ]

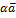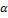4. [ + , ] = [ , ] + [ , ]

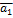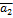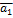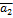М)-смешанное произведение

Смешанное произведение векторов , , 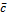в указанном порядке называется число: ([ , ], ).

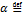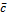Векторное пространство называется ориентированным, если в этом пространстве осуществлен выбор одного из двух классов одинаковых ориентированных базисов.

Н)-свойства смешанного произведения(2 леммы)

Свойства:

1. При циклической перестановке векторов базиса мы получаем базис той же ориентации что и исходной

2. Если 2 вектора базиса поменять местами, то получится новый базис противоположной ориентации.

Леммы:

1. Упорядоченная тройка некомпланарных , , 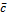векторов является правой тогда и только тогда, когда проекция на 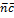>0.

n - ортогональный и ; , , 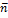- прав.

2. Если любой фиксированный вектор 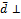любому вектору 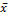=> =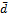0

Коментарий: При этом 2 и 3 условия бессмысленны, если хотя бы один из данных векторов является нулем.

Планиметрия

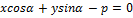– нормальное уравнение

а)-прямая на плоскости

Способы задания:

1) через 2 точки;

2) через пересеч. 2 плоскостей;

3) с помощью точки и направляющего вектора. MÎLóM0M = ta {x = x0 + tl; y = y0 + tm; z = z0 + tn} t = (x-x0)/l = (y-y0)/m = (z-z0)/k – каноническоеур-ние. (x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1) – в координатах.

Векторно-параметрическое уравнение прямой

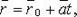где 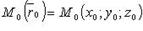- фиксированная точка, лежащая на прямой; 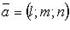- направляющий вектор.

В координатах (параметрические уравнения):

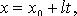
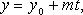
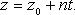
Канонические уравнения прямой

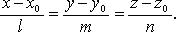
Уравнения прямой по двум точкам

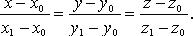
Прямая как линия пересечения двух плоскостей

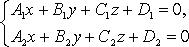
при условии, что не имеют места равенства

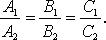
Взаимное расположение двух прямых

Если прямые заданы уравнениям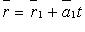и и 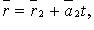то они:

1) параллельны (но не совпадают)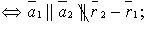

2) совпадают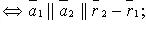

3) пересекаются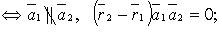

4) скрещиваются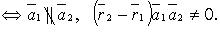

Если 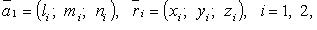то случаи 1 - 4 имеют место, когда ( 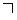- знак отрицания условия):

1)

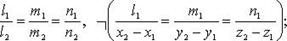
2)

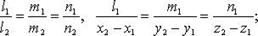
3)

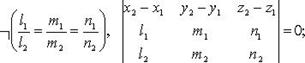
4)

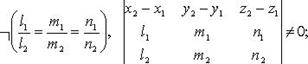
б)-плоскость в пространстве

Ax + By + Cz + D = 0 – общее ур-е плоскости

A(x-x0) + B(y-y0) + C(z-z0) = 0 – общее ур-ние плоскости, проходящей через точку M0.

xcosα + ycosβ + zcosγ = 0 – норм.ур-ние плоскости П.

{x = x0 + ua1 + vb1; y = y0 + ua2 + vb2; z = z0 + ua3 + vb3} – скалярное параметрическое ур-ние

Уравнение плоскости по трем точкам

В векторном виде

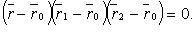
В координатах

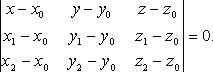
в)-прямая и плоскость в пространстве

г)-теорема определения места точек в пространстве

д)эллипс

Эллипсом называется ГМТ плоскости, сумма расстояний от каждой из которых до двух фиксированных точек плоскости F1 и F2, есть величина постоянная.

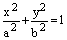- каноническое уравнение эллипса

Е)гипербола

Гипербола - ГМТ плоскости E², разность расстояний от каждой из которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная по модулю, меньшая расстояний между фокусами.

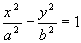- каноническое уравнение гиперболы

Ж)парабола

ГМТ плоскости E², равноудаленных от некоторой фиксированной точки F, называемой фокусом, и от некоторой фиксированной прямой D, называемой директрисой, называется параболой.

y² =2px - каноническое уравнение параболы

е)-геометрические объекты

ж)-алгебраические плоскости