СЛАУ. Определители. Матрицы.
СЛАУ. Определители. Матрицы.
СЛАУ- системы линейных алгебраических уравнений
а) -общие понятия
Система равенства  в которой
в которой  ,
,  носит
носит  ;
;  название СЛАУ содержащей n неизвестных
название СЛАУ содержащей n неизвестных  и состоящих из
и состоящих из  уравнений, при этом
уравнений, при этом  – коэффициент находящийся в i-строке и j-столбце, bi – свободный член.
– коэффициент находящийся в i-строке и j-столбце, bi – свободный член.
б) -общие определения решений
Решение СЛАУ (частного отдельно взятого) называется всякий упорядоченный набор чисел в общем случае вещественных состоящих из n вещ-х чисел α=( α1, α2,....., αn) αj  R при подстановке которых в уравнение системы вместо соответствующих неизвестных, каждое уравнение СЛАУ становится верным числовым неравенством(тождеством).
R при подстановке которых в уравнение системы вместо соответствующих неизвестных, каждое уравнение СЛАУ становится верным числовым неравенством(тождеством).
в) -системы: совместные/несовместные
Система называется совместной, если множество ее решений не пусто (если хотябы допускает одно решение) и несовместной в противном случае.
Совместная система называется определенной, если у нее есть одно решение и неопределенной в противном случае.
г)-коэффициенты. Неизвестные
a11x1 + a12x2 + ……+ a1nxn = b1} aij, bi – коэффициенты (действ. числа)
a21x1 + a22x2 + …... + a2nxn = b2} (1) aij – коэф. при неизвестных xj(ÎR или ÎС) 1≤i≤m, 1≤j≤n.
... ... ... …
am1x1 + am2x2 + … + amnxn = bm}m – число ур-ний, n – число неизвестных.
д)-расширенные матрицы
Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Или Ax=B
Е)-формы записи СЛАУ

1. СЛАУ(1)
2. Расширенная матрица
3. ∑nj=1 aijxj= bi (1≤ i ≤m)
4. A ∙ X=B
ж)-элементарные преобразования СЛАУ
1) перемена местами уравнений
2) умножение на любое число не равное 0
3) прибавление какого-либо уравнения, к другому уравнению предварительно умноженное на любое число.
4) добавление (отбрасывание) уравнения, тождества = 0
з)-элементарные преобразования СЛАУ (теорема).
В результате элементарных преобразований из СЛАУ(1) приводится к новой СЛАУ(2) равносильной исходной.
И)-эквивалентные матрицы
Системы СЛАУ 1 и 2 с одним и тем же числом неизвестных n называются равносильными (эквивалентными), если их множество решений совпадают.
К)-метод Гаусса
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам:
Шаг. Прямой ход метода Гаусса: приведение расширенной матрицы системы

к ступенчатому виду

с помощью элементарных операций над строками матрицы.
Шаг. Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица
 ,
,
последний, (n+1)-й, столбец этой матрицы содержит решение системы.
М)-алгоритмы
Алгоритм основан на след.фактах и понятиях:
1) на понятии элементарного преобразования СЛАУ
2) на теореме о том, что всякое элементарное преобразование переводит исходное СЛАУ к новой СЛАУ эквивалентной (равносильной) системе.
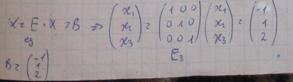
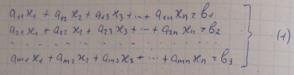
Алгоритм:
Не нарушая общности будем считать, что:
· Неизвестные x1 входит в 1-ре ур. сис. (по существу), т.е с ненулевым коэфицентом (а11ǂ0). Счиатя это предположение выполненным: исключаем неизвестное x1 из всех уравнений системы, кроме 1-ого.
· Неизвестное x1 из 2-ого уравнения:
Первое уравнение умножаем 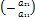 и результат прибавляем по 2-ому =˃
и результат прибавляем по 2-ому =˃

Пояснение: неизвестное х1исключено из всех, кроме 1-ого уравнения системы. При этом число уравнений может уменьшится или остаться неизменным.
г) Повторение 1-ого шага, но в системе:
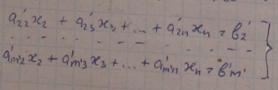
Оказывается при этом, в результате применения метода Гауса, возможны 3 исхода, к которым приводит этот метод:
1) заключается в том, что на каком-то шаге получается уравнение вида 0=b (≠0) - нет решений.
2) Матрица системы приводится к треугольному виду (к верхтреугольному) к такому, что на главной диагонали нет нулей. В этом случае получается единственное решение.
3)матрица системы приводится к виду трапеции
В этом случае системы имеет бесконечное число решений (множество решений)
О)-Виды матриц
Квадратная - n-го порядка называется матрица размера n×n.
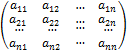
Прямоугольная- матрица размера mxn.
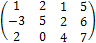
Диагональная (Квадратно-диагональная)-квадратная матрица, у которой все элементы вне главной диагонали равны нулю.
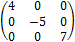
Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.
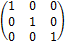
Нулевой называется матрица, все элементы которой равны нулю.
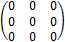
Скалярная - a ∙ En
П)-действия над матрицами
Сложение матриц. (Можно складывать матрицы одного и того же размера. Для сложения нужно сложить элементы стоящие на одних и тех же местах.)
Умножение матриц на число. (Можно умножить на любое число.Для этого нужно умножить каждый элемент на число.)
Умножение матрицы на матрицу(можно складывать любые две матрицы одинаковых размеров)
нужно чтобы совпадало число столбцов1-й матрицы и строк 2-й. Произведением матрицыАm×n на матрицуВn×p, называется матрицаСm×p такая, что
сik = ai1 × b1k + ai2 × b2k + ... + ain × bnk,
т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В.
Обратные матрицы (алгоритм)
Если дана произвольная матрица А
1) Составить Ат (транспортировочная матрица)
2) Найти алгебраическое дополнение к Ат
3) Составить А* (присоединенная матрица, союзная матрица для А)
4) Получить А-1 по формуле А-1=|1A| ∙ А* (|A| - детерминант матрицы А





 =
= 

n=1
A= (  =a)
=a)
 a
a 


h=2 





Т)-миноры
Минор матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк и столбцов.
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
У)-элементы комбинаторики
Произвольное расположение mсимволов, выбранных из n элементов называется размещение (Amn = n(n-1)*…*[n-(m-1)]). Всякое размещение из n по n приводит к понятию перестановки из n-символов (Pn= Ann = n(n-1)*…*2*1=1*2*3*…*(n-1)*n=n!) Если из множества n-символов выбирать подмножество из m-символов получается сочетание (Cmn = Amn/Pm = (Amn*Pnn-m)/(Pm*Pn-m) = Pn/(Pn*Pn-m)).
Ы)-свойства определителей
1- Определитель не меняется при транспозиции.
Замечание: Любое свойство для строк справедливо и для столбцов
2- Определитель содержащий строку из одних нулей, сам равен нулю
3- Если какую-либо строку определителя умножить на некоторое число, то и сам определитель умножается на это число.
4- Если поменять местами 2-ую строку, то определитель изменит знак на противоположный.
5- Если в определителе изменяются 2-е одинаковые строки, то он равен нулю.
6- Если в определителе имеются пропорциональные строки, то он равен нулю.
7- Если в определителе какая-либо строка представляет из себя сумму некоторых 2х пропорциональных матриц строк, тогда определитель равен сумме 2х определителей, у каждого из которых все строки кроме упомянутой те же самые, что и в исходном определителе.
8- Если к какой-либо строке определит любую другую его строку, предварительно умноженное на любое число, то определитель не изменится.
2.Геометрические векторы:
а)-свойства
1)  +
+  +
+ 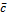 =
=  + (
+ (  +
+ 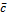 )- Ассоциативность сложения
)- Ассоциативность сложения
2) 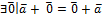 =
= 
3) 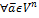 (n=0,1,2,3)
(n=0,1,2,3) 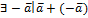 =
= 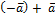 =0
=0
1-4 это абилева группа или коммутативная
4)  +
+  =
=  +
+  - Коммутативность сложения
- Коммутативность сложения
5) 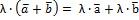 - Дистрибутивность умножения на число относительно сложения векторов
- Дистрибутивность умножения на число относительно сложения векторов
6) 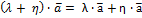 - Дистрибутивность умножения на число относительно сложения чисел
- Дистрибутивность умножения на число относительно сложения чисел
7) 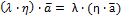 - Ассоциативность умножения на число
- Ассоциативность умножения на число
8) 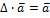
1-8 имеют место для любых  ,
,  ,
, 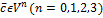
б)-линейные комбинации
Линейная комбинация – вектор  равен сумме произведений
равен сумме произведений 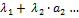
Вектор b = ∑mi=1λiai = λ1a1 + … + λmamназыв. линейной комбинацией векторов системы Am, а числа λ1, …, λmназыв. коэффиц. данной линейной комбинации.
Линейные комбинации называется тривиальной, если все ее коэффициенты = 0
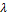 1 =
1 = 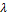 2 = ... +
2 = ... + 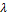 m = 0
m = 0
в)-зависимость(независимость)
Системы векторов Ам называется линейно зависимой, если сущ-ет нетривиальная линейная комбинация ее векторов = 0. В противном случае система Ам называется линейно-независимой.
Система Ам называется линейно независимой, если равенство 0 ее линейной комбинации возможно, только в тривиальном варианте.
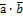 , b = -
, b = - 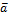 ,
, 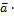 (-
(- 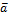 ) = 0 (комбинация не тривиальна, но она равна 0)
) = 0 (комбинация не тривиальна, но она равна 0)
Система Аm линейно зависима тогда и только тогда, когда один из векторов этой системы линейно выражается через остальные векторы этой же системы.
Система Am линейно независима тогда и только тогда, когда всякий вектор линейно выражающийся через нее единственен.
г)-критерии линейной независимости(док-во)
1) необходимость лин. зав. Пусть Am – лин-зав, т. е. $лин. нетрив. комб. ∑mi=1λiai=Ō λioaio + ∑mi=1(i≠io)λiai=Ō=>aio=∑mi=1(i≠io)μiai μi=–λi/λio 2) достаточность. Пусть вектор aioÎAm ∑mi=1λiai–1*aio= Ō Критерий лин. незав.: система векторов Amлин-незав. óякий вектор, линейно через нее выражающийся выражается через нее единственным способом. Док-во: 1) необходимость. Пусть Amлин-незав. a=∑mi=1λiai Пусть a=∑mi=1μiaia=∑mi=1(λi– μi)ai (λi– μi = γi) ∑mi=1 γiai= Ō => γi=0, т.е. λi= μi 2) достаточность. Пусть любой вектор, линейно-выражающийся через Am, т.е. такой, что a=∑mi=1λiai единств.образом. Ō=∑mi=1ηiai при ηi = 0 ∑mi=1λiai=Ō =>λi= μi =0
д)-базисы
Система векторов AmÌV называется полной, если всякий aÎV линейно выражается через векторы этой системы a=∑mi=1λiai.
Упорядоченная система векторов An=(a1, …,an) называется базисом векторного пространства V, если An – лин. незав. и полная.
1) Тривиальное пространство, сост. из Ō не имеет базиса.
2) Базис векторов на прямой – это любая система, сост. из одного ненулевого вектора.
3) Любая пара неколлинеарных векторов на плоскости образует базис.
4) Любая тройка некомпланарных векторов образует базис в пространстве.
Теорема. Если сущ. конечный базис An, n≠0 в векторном пространстве V, то любые два базиса состоят из одного и того же числа векторов.
Е)-размерности
Размерностью векторного пространства называется число векторов его базиса. (это опр. и теория формируются при условии. что выполняется аксиома размерности).
Аналитическая геометрия
а)-ориентация базиса
Пnn=0, 1, 2, 3
П0 – точка
П1 – прямая
П2 – плоскость
П3 – пространство
Vn – множество векторов на Пn
Vn – векторное пространство
(Пn,Vn) – аффинное пространство
dimVn=n
V1 – прямая линия
Говорят, что 2 базиса на прямой ( 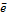 и
и 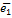 ) имеют одинаковую ориентацию, если коэффициент пропорциональности (
) имеют одинаковую ориентацию, если коэффициент пропорциональности ( 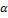 ) между ними больше нуля, в противном случае они имеют противоположную ориентацию.
) между ними больше нуля, в противном случае они имеют противоположную ориентацию.
Вращение по кротчайшему пути против часовой стрелки базис называется положительным или правым, по часовой стрелке базис называется левым.
Вращение по кротчайшему пути против часовой стрелки базис называется положительным или правым, по часовой стрелке базис называется левым.
Упорядоченная тройка некомпланарных векторов называется правой, если ее векторы расположены в том же порядке что и 3 пальца правой руки.
б)-декартовые координаты
в)-аффинные системы координат
Аффинная система координат (АСК) в Пn называется пара, состоящая из точки О и базиса 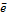 (О,
(О, 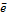 ) векторного пространства Vn.
) векторного пространства Vn.
Любой вектор в аффинном пространстве называется радиус-вектором (аффинной прямой).
Векторное или аффинное пространство, в котором введено скалярное произведение, является Евклидовым пространством.
г)-координаты точки
д)-прямоугольная Декарта
З)-направляющие углы
i, j, k – ОНБ (ортонормированный базис) ā = a1i + a2j + a3ka≠Ō В ОНБ i, j, k {ā*i = a1; ā*j = a2; ā*k = a3}(2) = {|ā|cos(a۸i) = a1; |ā|cos(a۸j) = a2; |ā|cos(a۸k) = a3} = {a1 = |ā|cosα; a2 = |ā|cosβ; a3 = |ā|cosγ}(3) α = ā۸i, β = ā۸j, γ = ā۸k. Косинусы углов α, β и γ назыв. направляющими косинусами вектора ā.
и)-косинусы векторов
К)-векторное произведение
Векторнымпроизведениемaнаbназываетсявекторc, что:
| 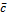 |=|
|=|  ||
||  |sin(
|sin(  ^
^  )
)
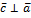 ,
, 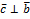
 ,
,  ,
, 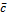 – правая
– правая
Замечание. Определение годится для неколлинеарных векторов aи b.
М)-смешанное произведение
Смешанное произведение векторов  ,
,  ,
, 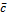 в указанном порядке называется число:
в указанном порядке называется число: 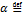 ([
([  ,
,  ],
], 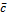 ).
).
Векторное пространство называется ориентированным, если в этом пространстве осуществлен выбор одного из двух классов одинаковых ориентированных базисов.
Планиметрия
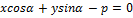 – нормальное уравнение
– нормальное уравнение
а)-прямая на плоскости
Способы задания:
1) через 2 точки;
2) через пересеч. 2 плоскостей;
3) с помощью точки и направляющего вектора. MÎLóM0M = ta {x = x0 + tl; y = y0 + tm; z = z0 + tn} t = (x-x0)/l = (y-y0)/m = (z-z0)/k – каноническоеур-ние. (x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1) – в координатах.
Векторно-параметрическое уравнение прямой
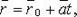 где
где 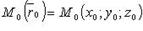 - фиксированная точка, лежащая на прямой;
- фиксированная точка, лежащая на прямой; 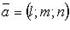 - направляющий вектор.
- направляющий вектор.
В координатах (параметрические уравнения):
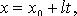
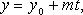
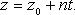
Канонические уравнения прямой
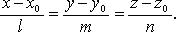
Уравнения прямой по двум точкам
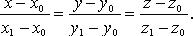
Прямая как линия пересечения двух плоскостей
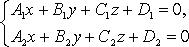
при условии, что не имеют места равенства
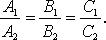
Взаимное расположение двух прямых
Если прямые заданы уравнениями 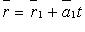 и
и 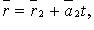 то они:
то они:
1) параллельны (но не совпадают) 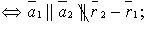
2) совпадают 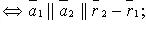
3) пересекаются 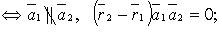
4) скрещиваются 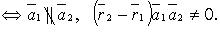
Если 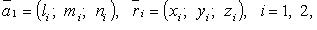 то случаи 1 - 4 имеют место, когда (
то случаи 1 - 4 имеют место, когда ( 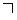 - знак отрицания условия):
- знак отрицания условия):
1) 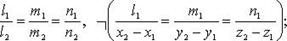
2) 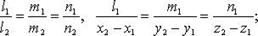
3) 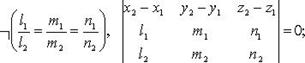
4) 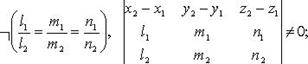
б)-плоскость в пространстве
Ax + By + Cz + D = 0 – общее ур-е плоскости
A(x-x0) + B(y-y0) + C(z-z0) = 0 – общее ур-ние плоскости, проходящей через точку M0.
xcosα + ycosβ + zcosγ = 0 – норм.ур-ние плоскости П.
{x = x0 + ua1 + vb1; y = y0 + ua2 + vb2; z = z0 + ua3 + vb3} – скалярное параметрическое ур-ние
Уравнение плоскости по трем точкам
В векторном виде
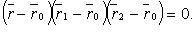
В координатах
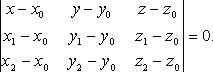
в)-прямая и плоскость в пространстве
г)-теорема определения места точек в пространстве
д)эллипс
Эллипсом называется ГМТ плоскости, сумма расстояний от каждой из которых до двух фиксированных точек плоскости F1 и F2, есть величина постоянная.
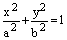 - каноническое уравнение эллипса
- каноническое уравнение эллипса
Е)гипербола
Гипербола - ГМТ плоскости E2, разность расстояний от каждой из которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная по модулю, меньшая расстояний между фокусами.
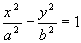 - каноническое уравнение гиперболы
- каноническое уравнение гиперболы
Ж)парабола
ГМТ плоскости E2, равноудаленных от некоторой фиксированной точки F, называемой фокусом, и от некоторой фиксированной прямой D, называемой директрисой, называется параболой.
y2 =2px - каноническое уравнение параболы
е)-геометрические объекты
ж)-алгебраические плоскости
СЛАУ. Определители. Матрицы.
СЛАУ- системы линейных алгебраических уравнений
а) -общие понятия
Система равенства  в которой
в которой  ,
,  носит
носит  ;
;  название СЛАУ содержащей n неизвестных
название СЛАУ содержащей n неизвестных  и состоящих из
и состоящих из  уравнений, при этом
уравнений, при этом  – коэффициент находящийся в i-строке и j-столбце, bi – свободный член.
– коэффициент находящийся в i-строке и j-столбце, bi – свободный член.
б) -общие определения решений
Решение СЛАУ (частного отдельно взятого) называется всякий упорядоченный набор чисел в общем случае вещественных состоящих из n вещ-х чисел α=( α1, α2,....., αn) αj  R при подстановке которых в уравнение системы вместо соответствующих неизвестных, каждое уравнение СЛАУ становится верным числовым неравенством(тождеством).
R при подстановке которых в уравнение системы вместо соответствующих неизвестных, каждое уравнение СЛАУ становится верным числовым неравенством(тождеством).
в) -системы: совместные/несовместные
Система называется совместной, если множество ее решений не пусто (если хотябы допускает одно решение) и несовместной в противном случае.
Совместная система называется определенной, если у нее есть одно решение и неопределенной в противном случае.
г)-коэффициенты. Неизвестные
a11x1 + a12x2 + ……+ a1nxn = b1} aij, bi – коэффициенты (действ. числа)
a21x1 + a22x2 + …... + a2nxn = b2} (1) aij – коэф. при неизвестных xj(ÎR или ÎС) 1≤i≤m, 1≤j≤n.
... ... ... …
am1x1 + am2x2 + … + amnxn = bm}m – число ур-ний, n – число неизвестных.
д)-расширенные матрицы
Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Или Ax=B
Е)-формы записи СЛАУ

1. СЛАУ(1)
2. Расширенная матрица
3. ∑nj=1 aijxj= bi (1≤ i ≤m)
4. A ∙ X=B
ж)-элементарные преобразования СЛАУ
1) перемена местами уравнений
2) умножение на любое число не равное 0
3) прибавление какого-либо уравнения, к другому уравнению предварительно умноженное на любое число.
4) добавление (отбрасывание) уравнения, тождества = 0
з)-элементарные преобразования СЛАУ (теорема).
В результате элементарных преобразований из СЛАУ(1) приводится к новой СЛАУ(2) равносильной исходной.
И)-эквивалентные матрицы
Системы СЛАУ 1 и 2 с одним и тем же числом неизвестных n называются равносильными (эквивалентными), если их множество решений совпадают.
К)-метод Гаусса
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам:
Шаг. Прямой ход метода Гаусса: приведение расширенной матрицы системы

к ступенчатому виду

с помощью элементарных операций над строками матрицы.
Шаг. Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица
 ,
,
последний, (n+1)-й, столбец этой матрицы содержит решение системы.
