Абсолютная и относительная погрешности. Определение количества верных значащих цифр в приближённом числе.
Абсолютная и относительная погрешности. Определение количества верных значащих цифр в приближённом числе.
Абсолютной погрешностью  приближенного числа а называется величина
приближенного числа а называется величина 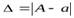 . Абсолютная погрешность - это разница между результатом измерения и истинным (действительным) значениемизмеряемой величины. Относительной погрешностью
. Абсолютная погрешность - это разница между результатом измерения и истинным (действительным) значениемизмеряемой величины. Относительной погрешностью  приближенного числа а назовем величину:
приближенного числа а назовем величину:
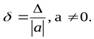
n – первых значащих цифр приближенного числа а являются верными, если абсолютная погрешность  этого числа не превышает ½ единицы разряда, выраженной n-ой значащей цифрой считая
этого числа не превышает ½ единицы разряда, выраженной n-ой значащей цифрой считая
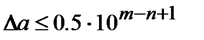
Где m - значение наибольшего разряда.
Правила округления приближённых чисел.
При округлении до z значащих цифр ошибка округления  ок не должна превышать точности вычислений и максимальной ошибки округления:
ок не должна превышать точности вычислений и максимальной ошибки округления:
 ок ≤ε
ок ≤ε  ок ≤max
ок ≤max 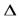 ок
ок
Правила вычисления погрешностей.
1)  А+В ≤
А+В ≤  А +
А +  В
В
2)  А+В <
А+В <  А-В
А-В
.  А+В =
А+В = 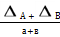
 А-В =
А-В = 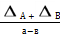
3)  А-В ≤
А-В ≤  А +
А +  В
В
4) 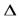 АВ ≤в*
АВ ≤в*  А +а*
А +а*  В
В  АВ ≤
АВ ≤  А+
А+  В
В
5)  А/В ≤
А/В ≤ 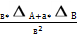
 А/В <
А/В <  А+
А+  В
В
Правила вычисления погрешностей функций и выражений.
1) метод прямых вычислений
2) метод среднего
Y=f(x);  y+=|f(x+
y+=|f(x+  x)-f(x)|;
x)-f(x)|;
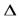 y-=|f(x-
y-=|f(x-  x)-f(x)|;
x)-f(x)|;  y=1/2(
y=1/2(  y+ +
y+ + 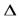 y-)
y-)
3) метод дифференциала
Y=f(x); dy≈Δy=|f ‘(x)|dx≈|f ‘(x)|Δx
Понятие о накоплении погрешностей при численном решении задач.
Общая погрешность: ε=εм+εок
Понятие устойчивости алгоритма вычислений.
Устойчивыми являются такие алгоритмы вычисления, для которых возникающие в процессе счета погрешности убывают или не возрастают в процессе получения решения. Для неустойчивых алгоритмов погрешности могут нарастать настолько быстро, что даже за небольшое количество шагов будет получаться совершенно неверный результат.
Отделение корня нелинейного уравнения, методы отделения корней.
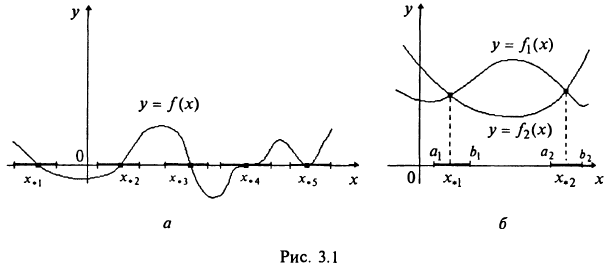
1) средствами машинной графики: функция представляется на дисплее и приближенно определяются отрезки, которым принадлежат точки (3.1а);
2) средствами математического анализа с помощью исследования функций и построения графиков;
3) формированием простых функций f1(x) f2(x) таких, что получается равносильное уравнение и дальнейшим построением графиков этих функций (3.1б).
Метод Крамера для решения систем линейных алгебраических уравнений.
Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
1. Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. Δ≠0.
- Для каждой переменной xi(i=1,2,…,n) необходимо составить определитель Δxi, полученный из определителя Δ заменой i-го столбца столбцом свободных членов заданной систем линейных алгебраических уравнений.
3. Найти значения неизвестных по формуле xi=ΔxiΔ (i=1,2,…,n).
Обусловленность систем линейных алгебраических уравнений.
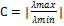 где С – степень обусловленности системы
где С – степень обусловленности системы
С=1-10 – хорошо обусловленная
С=10-103 – удовлетворительно обусловленная
С=103-105 – плохо обусловленная
 С>105 – вырожденная матрица
С>105 – вырожденная матрица
Уточнение решения системы линейных алгебраических уравнений.

Интерполирование функций.

Абсолютная и относительная погрешности. Определение количества верных значащих цифр в приближённом числе.
Абсолютной погрешностью  приближенного числа а называется величина
приближенного числа а называется величина 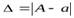 . Абсолютная погрешность - это разница между результатом измерения и истинным (действительным) значениемизмеряемой величины. Относительной погрешностью
. Абсолютная погрешность - это разница между результатом измерения и истинным (действительным) значениемизмеряемой величины. Относительной погрешностью  приближенного числа а назовем величину:
приближенного числа а назовем величину:
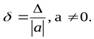
n – первых значащих цифр приближенного числа а являются верными, если абсолютная погрешность  этого числа не превышает ½ единицы разряда, выраженной n-ой значащей цифрой считая
этого числа не превышает ½ единицы разряда, выраженной n-ой значащей цифрой считая
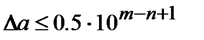
Где m - значение наибольшего разряда.
