Переход от одной системы координат к другой.
При исследовании свойств кривых 2-го порядка незаменимым подспорьем являются так называемые инварианты. Они задаются формулами (20), (21), (22).
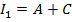 (20)
(20) 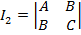 (21)
(21)
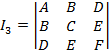 (22).
(22).
Инвариант в переводе на русский язык означает «неизменный». Дело в том, что как бы мы ни вращали координаты и ни переносили начало отсчёта, величины инвариантов не меняются, несмотря на то, что изменяются коэффициенты, входящие в матрицу (18а).
То есть, при повороте и сдвиге осей, из разных чисел, входящих в старую и новую матрицу коэффициентов, путем их подстановки в выражения для инвариантов получаются одни и те же числа. И свойства этих инвариантов определяют типы кривых: эллиптический, гиперболический, параболический.
Эллиптический тип: 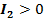 .
.
Если при этом не только 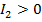 , но и
, но и 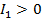 и
и 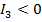 то кривая является эллипсом.
то кривая является эллипсом.
Гиперболический тип: 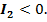
Если при этом не только 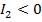 , но и и
, но и и 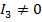 то кривая является гиперболой.
то кривая является гиперболой.
Параболический тип: 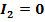 .
.
Если при этом не только 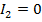 , но и
, но и 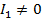 , и
, и 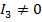 , то кривая является параболой.
, то кривая является параболой.
Эллиптический, гиперболический и параболический типы с инвариантами 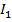 и
и 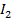 равными нулю, мы здесь не рассматриваем. Они дают вырожденные случаи, весьма отдалённо напоминающие эллипс, гиперболу или параболу. Информация на эту тему есть в математических справочниках.
равными нулю, мы здесь не рассматриваем. Они дают вырожденные случаи, весьма отдалённо напоминающие эллипс, гиперболу или параболу. Информация на эту тему есть в математических справочниках.
Если 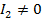 , тосистема двух уравнений с двумя неизвестными х0 и у0
, тосистема двух уравнений с двумя неизвестными х0 и у0
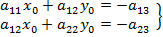 (23)
(23)
имеет единственное решение. Точка с координатами х0 и у0 и будет тем центром, куда следует поместить новое начало координат, чтобы исчезли слагаемые с первыми степенями. Другими словами, для эллипса и гиперболы всегда существует центр.
Поверхности 2-го порядка
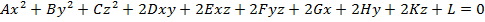 (24)
(24)
Или, что то же самое,
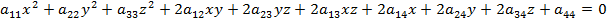
(25)
(24) и (25) – это тоже общее алгебраическое уравнение 2-го порядка, как и (18) и (19).

Но уже для трех переменных, а, значит, и определяет фигуры для 3-х мерного пространства. Оно, по аналогии с уравнением плоскости, задаёт поверхности в пространстве. Поверхности 2-го порядка уже сложнее и разнообразнее, чем плоскости. Все возможные плоскости интерпретируются как полученные из одной-единственной путём сдвигом и поворотов. С поверхностями 2-го порядка дела обстоят посложнее, но, всё-таки, это самые простые( в аналитическом смысле) представители искривлённых геометрических образов.
Для поверхностей 2-го порядка тоже существуют инварианты. Они задаются следующими формулами.
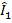 =
= 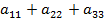 (26)
(26)
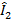 =
= 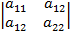 +
+ 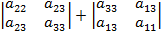 (27)
(27)
 (28)
(28)  (29)
(29)
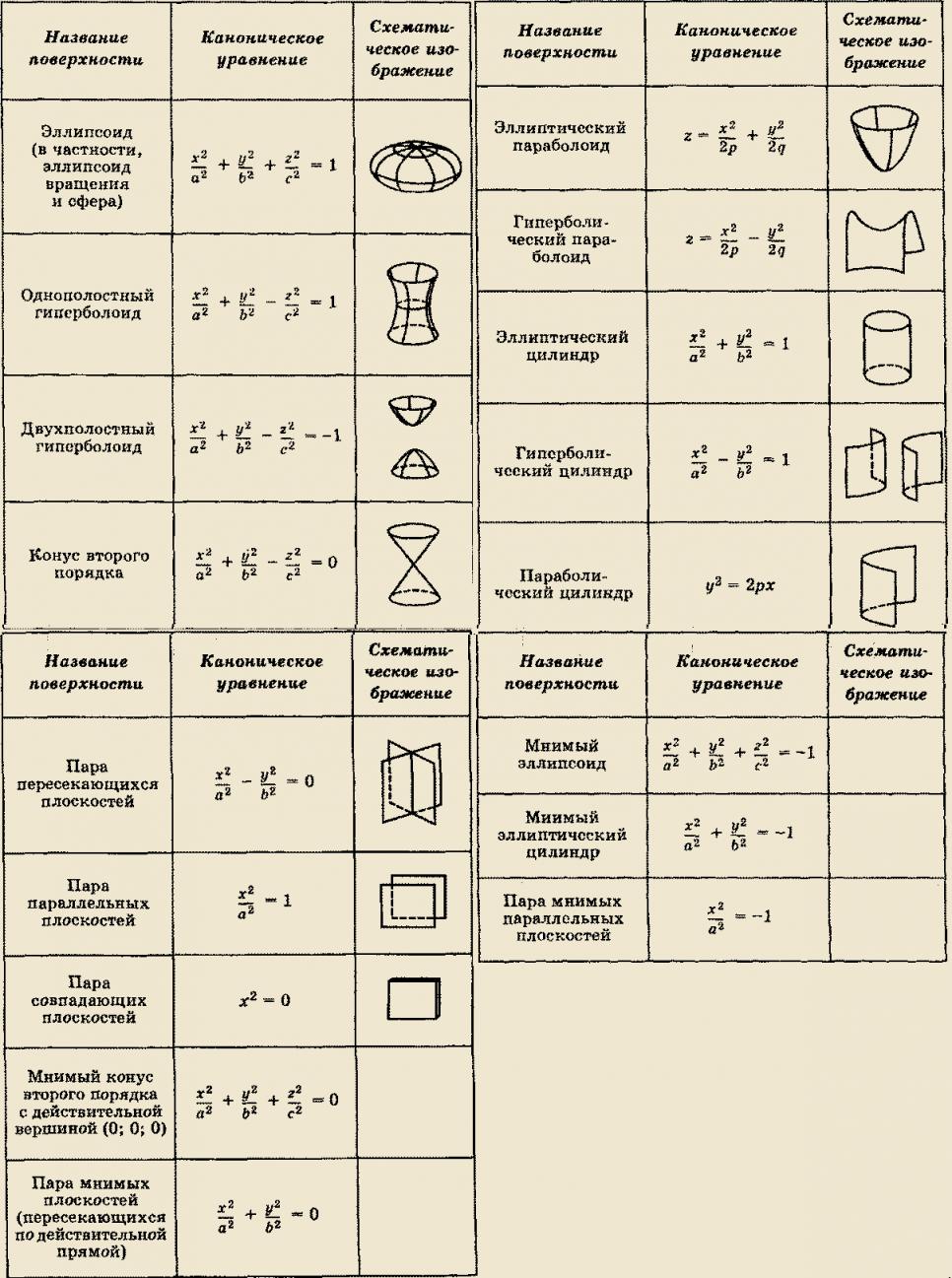
По инвариантам можно определить тип поверхности и привести уравнение к самому общепринятому (каноническому) виду.
По сравнению с двумерным случаем, разнообразие несколько увеличивается, и помимо ожидаемых эллипсоида, гиперболоида и параболоида появляются и такие фигуры как гиперболический параболоид, конус и различные цилиндры.
Как производить анализ таких фигур, можно найти в справочнике [Корн, Корн]. На данном этапе вам важно лишь усвоить принцип. В настоящее время красивый график для любого уравнения легко можно построить с помощью какой-либо компьютерной математической системы, например, Maple, Mathematica, MatLab. Эта лёгкость заметно снижает практическую ценность теории инвариантов для 2-х и 3-х мерных пространств.
Введение в матанализ
Важнейшие понятия
1. Число. Оно появляется в результате измерения. (Счёт тоже можно называть измерением.)
Служит для сравнения. А сравнение необходимо для того, чтобы сделать выбор, оказать предпочтение. Наша возможность что-либо аргументировано решать – весьма ограничена, пока мы не переходим к рассмотрению чисел. Числа можно изображать точками на числовой прямой. Длина отрезка, отложенного от нуля вправо, изображает положительное число, а отложенного влево от нуля – отрицательное число. Когда нам удобно, мы вместо чисел рассматриваем отрезки. От рассмотрения отрезков мы с легкостью перейдём к рассмотрению чисел, если так удобнее.
2.Переменная величина. Она принимает численные значения, но это не число! Назначение числа – твёрдо стоять на своём месте в ряду других чисел, полученных той же самой процедурой измерения. А переменная может принимать различные значения из диапазона.
3.Независимая переменная. Насекомое, которое летает в банке, каждый момент времени имеет произвольные координаты, ни от кого не зависимые.
4.Функция. Это величина, значения которой зависят от других величин. Она принимает те значения, которые ей назначено принимать. Функция в физике, химии, биологии – математическое описание закона природы. Закон одно разрешает, иное – запрещает.
Пример. Камень падает в колодец. Глубина падения, в зависимости от времени, меняется по закону 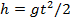 , и никак иначе.
, и никак иначе.
Функции задаются: графически, аналитически, таблично.
Аналитически – значит знаем алгоритм, как вычислить значение функции для данного аргумента ( Аргумент – та независимая переменная, от которой как раз и зависит функция.)
5.Последовательность. Это функция натурального аргумента. С помощью последовательностей вычисляют функции внутри калькулятора, и не только.
Примеры 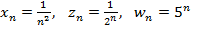 .
.
6. Предел последовательности. Это число а, такое, что начиная с некоторого n, все члены последовательности попадают в сколь угодно малую окрестность этого числа а .
7.Неперывность функции. Функция f(x) называется непрерывной в точке x=a, если 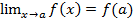 . Функция f(x) называется непрерывной на отрезке, если она непрерывна в каждой точке х, принадлежащей отрезку.
. Функция f(x) называется непрерывной на отрезке, если она непрерывна в каждой точке х, принадлежащей отрезку.
8.Бесконечно малые функции. Функция f(x) называется бесконечно малой в окрестности точки x=a, если 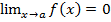 . Функция f(x) называется бесконечно малой более высокого порядка малости, чем функция g(x), если
. Функция f(x) называется бесконечно малой более высокого порядка малости, чем функция g(x), если 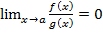
Примеры. Функция f(x)=х3 при 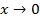 и функция g(x)=х2.
и функция g(x)=х2. 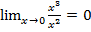 .
.
