Линейные образы в пространстве

По аналогии с (1) уравнение плоскости запишется:

A x + B y + C z + D = 0 (11)

Все точки с координатами x, y, z, удовлетворяющими уравнению (11), принадлежат данной плоскости.

Прямая линия в пространстве задаётся пересечением плоскостей:

A x + B y + C z + D = 0 и A₁ x + B₁ y + C₁ z + D₁ = 0.

Чтобы задать точку, эту прямую надо пересечь ещё одной плоскостью:

A₂ x + B₂ y + C₂ z + D₂ = 0.

Трём различным плоскостям соответствует система трёх уравнений с тремя неизвестными:

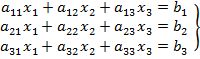(12)

Здесь сразу записали способом, экономящим буквы.

Плоскости тоже являются линейными образами, так как в выражения входят суммы переменных, умноженных на константы, так же как и в уравнении прямой линии.

Геометрическая интерпретация, что такое решение системы (12):

Система (12) имеет решение, если существует точка {x₁,x₂,x₃}, принадлежащая сразу всем трём плоскостям.

Известно, что если плоскости пересекаются, то у них есть общая прямая. Чтобы существовала точка, принадлежащая сразу трём плоскостям, эта прямая должна пересекаться третьей плоскостью. Очевидно, что такое происходит далеко не всегда.

Могут быть еще и такие случаи:

2.Все три плоскости сливаются.

3.Две плоскости сливаются, третья их пересекает.

В случаях 2. и 3. система имеет бесконечное множество решений.

4.Все три плоскости параллельны. В этом случае система не имеет решений.

В пространстве вдоль трёх осей вводят три базисных вектора: i , j, k. Принципиальной теоретической необходимости в этом нет, но это даёт большие дополнительные преимущества для представления различных задач в удобном виде.

x = 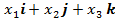- так запишется некий свободный вектор в пространстве, или, иначе:

x = .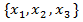

Скалярное произведение векторов в пространстве:

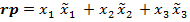
Складываются и умножаются вектора в пространстве, точно так же, как и на плоскости. И скалярное произведение вводится так же. И, когда мы введём понятие мерного пространства, эти формулы будут аналогичны.

В пространстве задаётся и векторное произведение:

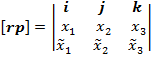(13)

В формуле (13) в прямых скобках стоит определитель 3-го порядка, смысл которого рассмотрим в дальнейшем. Понятие определителя введено также из потребности иметь компактные записи.

Векторное произведение – это новый вектор, перпендикулярный плоскости, в которой лежат исходные два. Численно его длина равна площади параллелограмма, построенного на исходных векторах.

Векторное произведение описывает в механике момент импульса, кориолисово ускорение,

момент силы, в электродинамике - силу Лоренца, и многие другие физические законы.

Формула (13) очень убедительно иллюстрирует удобство от введения базисных векторов.

Без них формула (13) выглядит гораздо более громоздко.

Наука, изучающая геометрические объекты с помощью формул, называется аналитической геометрией.

А наука, черпающая идеи из геометрии (размерность 3) и переносящая их на N-мерные объекты, называется линейной алгеброй.

В линейной алгебре основным понятием является понятие линейной комбинации. Оно является своеобразным мостиком между указанными двумя науками.

Поясним это понятие с помощью трёхмерного пространства.

Уравнение (12) можно представить как выражение вектора свободных членов через комбинацию вектор столбцов, где неизвестные являются числовыми коэффициентами. Такая, и похожие на неё комбинации называются линейными, так как по своему внешнему виду напоминают уравнение прямой линии.

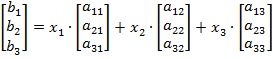(Linear Combination)

Векторы и другие фигуры в N-мерном пространстве представить зрительно невозможно, но их математические формулы весьма похожи на таковые для трёхмерного пространства.

Поэтому поступают следующим образом: формулы пишут для пространства произвольной размерности, а иллюстрации рисуют для 2-х или 3-х мерного пространства.

С позиции линейной комбинации задачу о решении системы линейных уравнений (12) можно представить таким образом: как подобрать коэффициенты {x₁, x₂, x₃}, чтобы выразить один вектор через три других?

Введение базиса из трёх векторов i, j, k – попытка представить любой вектор как линейную комбинацию базисных. Такая попытка в трёхмерном пространстве всегда удаётся.

Другое важнейшее понятие – линейная зависимость. Набор векторов называется линейно зависимым, если любой из этого набора можно выразить как линейную комбинацию остальных.

В трёхмерном пространстве любой вектор можно представить как линейную комбинацию трёх базисных, а в любом N-мерном – как линейную комбинацию из N штук базисных векторов.