Теорема сложения вероятностей произвольных событий

Вероятность суммы двух произвольных событий равна разности суммы и произведения вероятностей этих событий:

P(A + B) = P(A) + P(B) - P(AB).

Следствие. Вероятность суммы произвольных событий никогда не превосходит суммы вероятностей этих событий:

P(A₁ + A₂ +...+ A_n) ≤ P(A₁) + P(A₂) +...+P(A_n).

Теорема сложения несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B).

Следствие. Вероятность суммы конечного числа попарно несовместных событий равна сумме вероятностей этих событий:

P(A₁ + A₂ +...+ A_n) = P(A₁) + P(A₂) +...+P(A_n).

Условные вероятности и независимые события

Вероятность события А при условии, что произошло событие В, называется условной> вероятностью события А и обозначается как

P(A|B) = PB(A).

Если при вычислении вероятности Р(А) никаких ограничений, кроме условий Ψ не налагается, то такие вероятности называются безусловными. Строго говоря, безусловные вероятности также являются условными, поскольку исходным моментом их определения было предположение о существовании некоторого неизменного комплекса условий Ψ.

Определение 2. Два события А и В называются независимыми, если вероятность каждого из них не зависит от появления или непоявления другого, т.е.

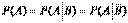и .

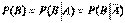В противном случае события называются зависимыми.

Теорема умножения вероятностей произвольных событий.

Вероятность произведения двух произвольных событий равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое имеет место, т.е.

P(AB) = P(A)P(B|A) = P(B)P(A|B).

Следствие. Для любых двух событий А и В справедливо равенство

P(A)P(B|A) = P(B)P(A|B).

Теорема умножения произвольных событий допускает обобщение на случай нескольких событий.

Теорема умножения независимых событий. Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий:

P(AB) = P(A)P(B).

Теорема умножения независимых в совокупности событий. Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий:

P(A1 x A2 x...x An) = P(A1) x P(A2) x...x P(An).

Формула полной вероятности

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно ,

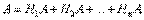
Применяя аксиому сложения вероятностей, имеем

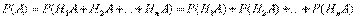
Но 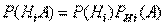(i=1, 2, ..., n), поэтому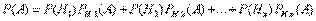

Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».

Формула Байеса

Пусть событие 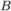происходит одновременно с одним из 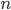несовместных событий 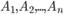. Требуется найти вероятность события 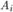, если известно, что событие произошло.

На основании теоремы о вероятности произведения двух событий можно написать

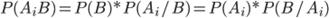
Откуда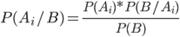

или 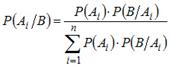(3.2)

Формула (3.2) носит название формулы Байеса.