Раздел 1.Теория вероятностей

Раздел 1.Теория вероятностей

1.Случайные события и вероятности

1.1.1.Предмет теории вероятностей.

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Опыт-это явление, происходящее при условиях, созданных человеком и которое может повторяться большое кол. раз. Результатом опыта наз. случайным событием.

Виды случайных событий

1.достоверные Е(событие, кот. в усл. данного опыта обязательно происходит)

2.невозможное U(никогда не происходят в усл. данного опыта)

3.несовместные(если в усл данного опыта не происх. одновременно)

4.совместные(в условиях данного опыта м. появиться одновременно)

5.В благопрепятствует А,если из факта появленияВ вытекает факт появления А.

6.А и Ас чертой,к каждому событию А мож. сопоставить противопол. события, т.е такое событие, кот дополн А)

1.1.2. Вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений.

n-опыт ,m,a-число опытов,при кот.события происх.

M(A)/n=ω(A)-частота проведения опытов

Классическое и статистическое определение вероятности

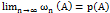–теорема Бернулли или статистическая вероятность события А

Классическая формула вероятности.

Обознач набором элементов исх.опыта.-наз. Множество событий{ 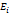}i=1

1.в результате опыта обязат. Происх одно из данных событий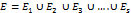

2.события 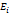попарно несовместны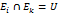

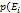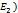3.статистич вероятность всех событий равны. )=p( =…=p( )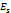

Геометрическая вероятность

Если пространство элементарных событий содержит бесконечное множество элементов и ему можно поставить в соответствие некоторое геометрическое пространство, а вероятность каждого события зависит только от меры этого события, а не от его положения, то говорят, что на этом пространстве определена геометрическая вероятность. При этом вероятность каждого события А есть отношение меры А к мере U пространства элементарных событий. Под мерой понимается

-в одномерном пространстве - длина

-в двумерном пространстве - площадь

-в трехмерном пространстве - объем

Таким образом, геометрическая вероятность означает, что :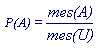

Действия над событиями

1. Если при всяком испытании, при котором происходит событие А, происходит и событие B, то событие А называется частным случаем события B.
А М B или B Й A

2. Событие (А и B), т. е. событие, состоящее в наступлении обоих событий А и B, называется произведением событий А и B и обозначается через

АB

3. Событие (А или B), т. е. событие, состоящее в наступлении хотя бы одного из событий А и B, называется суммой событий А и B и обозначается через

А + B

4. Событие, состоящее в том, что событие А не происходит, называется противоположным событию А и обозначает- ся через .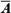
5. Событие (А и 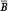), состоящее в том, что A происходит, а B не происходит, называется разностью событий А и B и обозначается через

А - B

Формула полной вероятности

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно ,

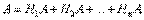
Применяя аксиому сложения вероятностей, имеем

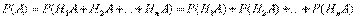
Но 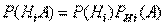(i=1, 2, ..., n), поэтому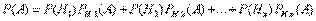

Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».

Формула Байеса

Пусть событие 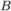происходит одновременно с одним из 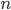несовместных событий 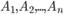. Требуется найти вероятность события 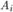, если известно, что событие произошло.

На основании теоремы о вероятности произведения двух событий можно написать

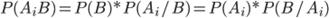
Откуда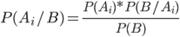

или 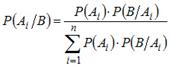(3.2)

Формула (3.2) носит название формулы Байеса.

Формулы Бернулли

Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность Pk,n того, что событие A наступит k раз в n независимых испытаниях, равна: ,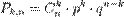

где q = 1-p

Локальная теорема Лапласа.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

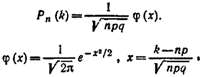
Для определения значений φ(x) можно воспользоваться специальной таблицей.

Интегральная теорема Лапласа.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь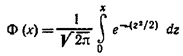

-функция Лапласа

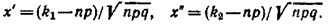
Значения функции Лапласа находят по специальной таблице.

Теорема Пуассона

При большом количестве испытаний вычисления по формуле Бернулли становятся затруднительными. Однако в ряде случаев их можно заменить более простыми асимптотическими формулами. Одна из них основана на теореме Пуассона.

Если число испытани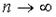й и 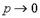так, ч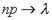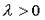то , , то 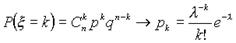при любых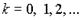

Это означает, что при больших nи малых p вместо вычислений по точной формуле

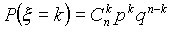
можно воспользоваться приближенной формулой ,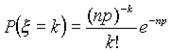

т.е. использовать формулу Пуассона для l =np.

Понятие случайной величины.

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.2 типа СВ: Дискретная-СВ,принимающая конечное или бесконечн.счетное множ-во значений. Например:частота попаданий при трех выстрелах;число бракованных изделий в партии из n штук; число вызовов, поступающих на телефон.станцию в течение суток; возможн.число горошин в 1 кг.

Непрерывная-СВ, кот. м.принимать люб.значения из некоторого конечн. или бесконечн.интервала.. Например: ошибка при измерении дальности радиолокатора;время безотказной работы микросхемы; погрешность изготовл-я деталей;концентрация соли в морской воде. Для задания случайной величины надо перечислить все ее возможн. значения и вероятности их появления. Совокупность всех возможн.знач-ий СВ и соответствующих им вероят-тей – распредел-е СВ.

Дискретные СВ- величина, кот.в рез-те испытаний принимает то или иное(только одно)возможн.значение,заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайн.обстоятельств. В отличие от случайн.события,кот. явл-ся качественной характеристикой случайн. рез-та испытания,случайн.величина характеризует рез-т испытания колич-но. Примеры: размер обрабатываемой детали,погрешность рез-та измерения к-л параметра изделия или среды.

Примеры распределений ДСВ:

Биномиальное распределение-распр-е кол-ва «успехов» в последоват-ти из n независимых случайн.экспериментов, таких что вероятность «успеха» в каждом из них одинакова.

фор-ла Бернулли: 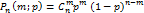, где p-вероят-ть,n-число испытаний, m-число появл-ий соб.А

Мат.ожид-е: 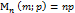, Дисперс.: 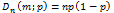прим. Вероятность поломки одного из пяти работающих независимо друг от друга станков = 0,2. Если происходит поломка, станок до конца дня не работает. Какова вероятность, что 0, 1, 2, 3, 4, 5 станков сломаются в течение дня?Решение: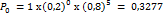

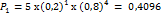и.т.д

Распред-е Пуассона-моделирует СВ, представляющую собой число событий, произошедших за фиксир-е время, при условии, что данные события происходят с нек. фиксиро-й средн.интенсивностью и независ.друг от друга (число испытаний -оч.велико, вероят.появл. соб. А-оч.мала) Фор-ла Пуассона: 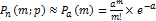(a=n*p)

Мат.ожид-е: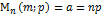

Дисперс.: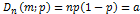

прим.:на АТС в теч-е 1 часа поступило n=500 сигналов.Вероят-ть сбоя p=0,002.Написать 5 первых членов закона распр-я.Решение: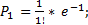

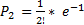и т.д.

Геометри́ч-е распред-е- распред-е дискретн.случайн. величины равной колич-ву испытаний случайн. эксперимента до наблюдения 1-го «успеха».

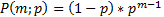где m-число испыт-ий

Мат.ожид-е: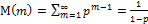

Дисперс.: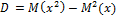

Прим.2стрелка поочерёдно стреляют по целям до 1-го попадания одного из орудий. Вероят-ть попадания 1-ым стрелком=0,7; 2-ым=0,8.Вначале стреляет 1-ый стрелок. Сост-ть 1-ые 5 членов распр-я. Реш-е: P(1)=0,7; Р(2)=0,3*0,8; Р(3)=0,3*0,2*0,7 и т.д.

Гипергеометрическое рас-е-моделирует кол-во удачных выборок без возвращения из конечн.совокупности.

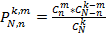Прим.В партии из N=20 изелий n=5 изд. имеют дефект.Какова вероят-ть,что из взятых m=4 изд. k=2 изд-я явл-ся дефектными? Реш.: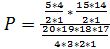

Числовые характер-ки ДСВ

Мат.ожидание - сумма произведений всех возможн.значений случайн.величины на их вероятности.(для усредненной оценки нек.случайн.значения).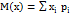

Св-ва мат.ожид-я: 1)Мат. ожид-е по­стоянной величины=самой постоянной: М(С) = С; 2)Постоянный множитель можно выно­сить за знак мат.ожидания: М(СХ) = СМ(Х). 3)Мат.ожид-е произведе­ния 2х независим. СВ = произведе­нию мат.ожиданий сомножителей M(XY) = M(X)·M(Y). 4)Мат.ожидание суммы (разности) 2х СВ = сумме(разности) их мат.ожиданий слагаемых. M(X 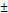Y) = M(X) 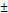M(Y); Мат. Ожидание числа появления события в независимых испытаниях.Мат.ожидание М(Х) числа появления соб.А в n независим.испытаниях=произвед-ю числа испытаний на вероят-ть появления события в кажд. испытании.:M(X)= np . Дисперсия -степень разброса значений случ.величины относит-но её мат.ожидания. D(x) = M(x2) – (M(x))

Св-ва дисперсии 1.Дисперсия постоян.величины равна 0: D (С)=0; 2.Постоян. множитель можно выно­сить за знак дисперсии, возводя его в квадрат: D(CX)-C2 ·D(X).3.Дисперсия суммы 2х независим. СВ = сумме дисперсий этих величин: D (X + Y) = D (X) + D (У) 4. Дисперсия разности 2х независим. СВ = сумме их дисперсий: D (X – Y) = D (X) + D (У).

Дисперсия числа появлений события в независим.испытаниях:Пусть производится п независим. испытаний, в каждом из кот. вероят-ть появления события А постоянна и равна p.Тогда дисперсия числа появлений со­бытия в этих испытаниях вычисл-ся по фор-ле: D(Х)=npq, n–число испыт-ий, p–вероят-ть наступления события, q-вероят-ть не наступления события.

Средн.квадратич-е отклонение-квадратн.корень из дисперсии (когда надо, чтобы оценка рассеяния имела размерность слу­чайн.величины)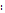

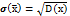Функц-я распред-я F(x) называется вероят-ть того, что случайн. величина X примет знач-е, меньшее х: F(x) = F (x) = P(Х< x) .

Одинаково распредел-е взаимно независим.СВ Мат.ожидание ср.арифметич-го одинаково распредел.взаимно независ.СВ= мате. ожиданию каждой из этих величин: М( 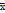)=М. Дисперсия ср.арифметич-го n один-во распредел-х взаимно независим. СВ в n раз меньше дисперсии кажд.из этих величин:D( 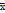)=D/n.Средн. квадратич.отклонение средн.арифметич-го n одинаково распредел-х взаимно независим.СВ в 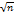раз меньше средн.квадратич. отклонения кажд.из этих величин: ( )= / .

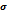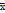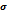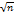1.2.4.Закон больших чисел

Закон больших чиселв теории вероятностейутверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Неравенство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего.

Теорема Чебышёва. Для независимых случайных величин 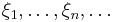соотношение

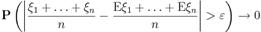
(при любом 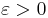и 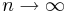) верно при весьма общих предположениях:

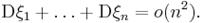
Сущность теоремы Чебышева заключается в том, что хотя каждая из независимых Случ Величин 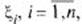может принять значение, далекое от 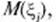среднее арифметическое 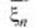при достаточно большом п с большой вероятностью будет весьма близко к 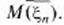Несмотря на то, что отдельные попарно независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа этих величин с большой вероятностью принимает значения, близкие к определенному постоянному числу – среднему арифметическому их математических ожиданий. Другими словами, хотя отдельные случайные величины могут иметь значительный разброс, их среднее арифметическое рассеяно мало. Практическое значение этого факта заключается в том, что можно принять в качестве искомого значения некоторой измеряемой величины среднее арифметическое результатов нескольких измерений.

Теорема Бернулли

Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность P_{k, n} того, что событие A наступит k раз в n независимых испытаиях, равна: 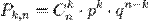где q = 1-p.

Теорема Ляпунова

Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Пусть 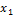, , 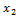…, , …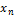- неограниченная последовательность независимых случайных величин с математическими ожиданиями 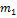, , 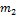…, , … 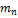и дисперсиями 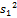, , 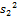…, … 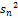. Обозначим , , ,.

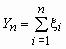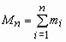
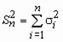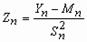Тогда 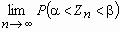= Ф(b) - Ф(a) для любых действительных чисел a и b , где Ф(x) - функция распределения нормального закона.

Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

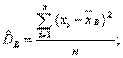
если же все значения имеют частоты n₁, n₂,…,n_k, то

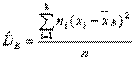
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

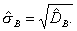
Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

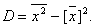
Замечание: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Исправленная дисперсия.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

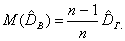
Для исправления выборочной дисперсии достаточно умножить ее на дробь

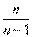
получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

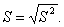
Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

2.2.2. Интервальные оценки параметров нормального распредления

Интервальной называют оценку, которая определяется двумя числами—концами интервала, покрывающего оцениваемый параметр.

Оценка точности измерений

В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения дисперсии случайных ошибок измерений. Для оценки дисперсии используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то теория, Доверительный интервал для оценки дисперсии и среднего квадратического отклонения, применима для оценки точности измерений.

Раздел 1.Теория вероятностей

1.Случайные события и вероятности

1.1.1.Предмет теории вероятностей.

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Опыт-это явление, происходящее при условиях, созданных человеком и которое может повторяться большое кол. раз. Результатом опыта наз. случайным событием.

Виды случайных событий

1.достоверные Е(событие, кот. в усл. данного опыта обязательно происходит)

2.невозможное U(никогда не происходят в усл. данного опыта)

3.несовместные(если в усл данного опыта не происх. одновременно)

4.совместные(в условиях данного опыта м. появиться одновременно)

5.В благопрепятствует А,если из факта появленияВ вытекает факт появления А.

6.А и Ас чертой,к каждому событию А мож. сопоставить противопол. события, т.е такое событие, кот дополн А)

1.1.2. Вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений.

n-опыт ,m,a-число опытов,при кот.события происх.

M(A)/n=ω(A)-частота проведения опытов

Классическое и статистическое определение вероятности

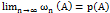–теорема Бернулли или статистическая вероятность события А

Классическая формула вероятности.

Обознач набором элементов исх.опыта.-наз. Множество событий{ 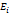}i=1

1.в результате опыта обязат. Происх одно из данных событий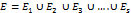

2.события 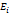попарно несовместны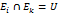

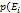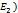3.статистич вероятность всех событий равны. )=p( =…=p( )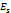

Геометрическая вероятность

Если пространство элементарных событий содержит бесконечное множество элементов и ему можно поставить в соответствие некоторое геометрическое пространство, а вероятность каждого события зависит только от меры этого события, а не от его положения, то говорят, что на этом пространстве определена геометрическая вероятность. При этом вероятность каждого события А есть отношение меры А к мере U пространства элементарных событий. Под мерой понимается

-в одномерном пространстве - длина

-в двумерном пространстве - площадь

-в трехмерном пространстве - объем

Таким образом, геометрическая вероятность означает, что :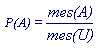

Действия над событиями

1. Если при всяком испытании, при котором происходит событие А, происходит и событие B, то событие А называется частным случаем события B.
А М B или B Й A

2. Событие (А и B), т. е. событие, состоящее в наступлении обоих событий А и B, называется произведением событий А и B и обозначается через

АB

3. Событие (А или B), т. е. событие, состоящее в наступлении хотя бы одного из событий А и B, называется суммой событий А и B и обозначается через

А + B

4. Событие, состоящее в том, что событие А не происходит, называется противоположным событию А и обозначает- ся через .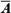
5. Событие (А и 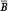), состоящее в том, что A происходит, а B не происходит, называется разностью событий А и B и обозначается через

А - B