Методы численного интегрирования: постановка задачи, методы Монте–Карло.

Вычисление кратных интегралов можно осуществлять повторным применением алгоритмов рассмотренных выше, но при этом увеличивается объем вычислительной работы. В этом случае могут быть применены статистические методы, хотя они и имеют не достаточно высокую точность. К таковым относят методы Монте-Карло.

Рассмотрим два варианта их этих методов.

Первый вариант

Его можно интерпретировать как статистический вариант метода прямоугольников (рисунок 3). Только в качестве узла x₀ берется случайное число, равномерно распределенное на интервале интегрирования 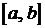. Вследствие случайного узла x₀ погрешность интеграла также будет носить случайный характер.

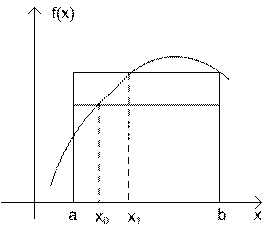
Рисунок 3

Проведя N вычислений со случайными узлами x_i результат усредняется и усредненное значение принимается за приближенное значение интеграла (4.6.1):

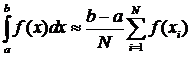(4.6.1)

Погрешность интеграла будет уменьшаться с ростом числа испытаний N по закону .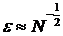

Второй вариант

Вычисляемый интеграл приводится к виду (4.6.2)

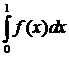(4.6.2)

где 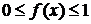на интервале 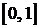. Тогда две случайные величины x_i и x_j можно рассматривать как координаты точек в единичном квадрате. При равномерном распределении точек в квадрате за приближенное значение интеграла принимается отношение количества точек S, попавших под кривую y=f(x) к общему числу испытаний N (4.6.3) (рисунок 4):

(4.6.3)

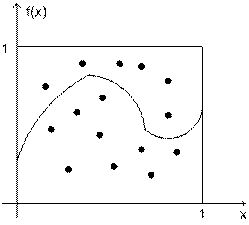
Рисунок 4

Решение математических задач в EXCEL.

Нахождение обратной матрицы:

МОБР

Возвращает обратную матрицу для матрицы, хранящейся в массиве.

Синтаксис

МОБР(массив)

Массив — числовой массив с равным количеством строк и столбцов.

Заметки

Массив может быть задан как диапазон ячеек, например A1:C3; как массив констант, например {1;2;3: 4;5;6: 7;8;9}; или как имя диапазона или массива.

Если какая-либо из ячеек в массиве пуста или содержит текст, то функция МОБР возвращает значение ошибки #ЗНАЧ!.

МОБР также возвращает значение ошибки #ЗНАЧ!, если массив имеет неравное число строк и столбцов.

Формулы, которые возвращают массивы, должны быть введены как формулы массива.

Обратные матрицы, как и определители, обычно используются для решения систем уравнений с несколькими неизвестными. Произведение матрицы на ее обратную — это единичная матрица, то есть квадратный массив, у которого диагональные элементы равны 1, а все остальные элементы равны 0.

В качестве примера того, как вычисляется обратная матрица, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В следующей таблице приведена обратная матрица для A1:B2:

	Столбец A	Столбец B
Строка 1	d/(a*d-b*c)	b/(b*c-a*d)
Строка 2	c/(b*c-a*d)	a/(a*d-b*c)

МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к небольшим численным ошибкам округления.

Некоторые квадратные матрицы не могут быть обращены, в таких случаях функция МОБР возвращает значение ошибки #ЧИСЛО!. Определитель такой матрицы равен 0.

Пример 1

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

Создайте пустую книгу или лист.

Выделите пример в разделе справки. Не выделяйте заголовок строки или столбца.

Выделение примера в справке.

Нажмите сочетание клавиш CTRL+C

На листе выделите ячейку A1 и нажмите сочетание клавиш CTRL+V.

Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите сочетание клавиш CTRL+` (апостроф) или в меню Сервис укажите на пункт Зависимости формул и выберите режим Режим проверки формул.

A B Данные Данные -1 Формула Формула =МОБР(A2:B3)

Примечание. Формулу в этом примере необходимо ввести как формулу массива. После копирования этого примера на пустой лист выделите диапазон A5:B6, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем нажмите клавиши CTRL+SHIFT+ENTER. Если формула не будет введена как формула массива, единственное значение будет равно 0.

Пример 2

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

Создайте пустую книгу или лист.

Выделите пример в разделе справки. Не выделяйте заголовок строки или столбца.

Выделение примера в справке.

Нажмите сочетание клавиш CTRL+C

На листе выделите ячейку A1 и нажмите сочетание клавиш CTRL+V.

Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите сочетание клавиш CTRL+` (апостроф) или в меню Сервис укажите на пункт Зависимости формул и выберите режим Режим проверки формул.

A B C Данные Данные Данные -1 Формула Формула Формула =МОБР(A2:C4)

Примечание. Формулу в этом примере необходимо ввести как формулу массива. После копирования этого примера на пустой лист выделите диапазон A6:C8, начиная с ячейки, содержащей формулу. Нажмите клавишу F2, а затем нажмите клавиши CTRL+SHIFT+ENTER. Если формула не будет введена как формула массива, единственное значение будет равно 0,25.

Совет Для доступа к отдельным элементам обратной матрицы следует использовать функцию ИНДЕКС.

ИНДЕКС

Возвращает значение или ссылку на значение из таблицы или интервала. Функция ИНДЕКС () имеет две синтаксические формы: ссылка и массив. Ссылочная форма всегда возвращает ссылку; форма массива всегда возвращает значение или массив значений.

ИНДЕКС(массив;номер_строки;номер_столбца) возвращает значение указанной ячейки или массив значений в аргументе «массив».

ИНДЕКС(ссылка ;номер_строки;номер_столбца;номер_области) возвращает ссылку на указанные ячейки или ячейки в аргументе «ссылка».