Решение задач на геометрическое определение вероятности
| 3.1. Разобрать решение задач, заполнив пропуски | |||||||||||||||||||||||||||||||
Задача1. На отрезке единичной длины случайным образом появляется точка. Найти вероятность того, что расстояние от точки до концов отрезка больше 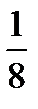 . Решение. . Решение. 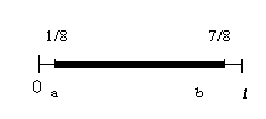
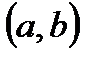 . . Его длина Значит, искомая вероятность | |||||||||||||||||||||||||||||||
Задача 2.В круг радиуса 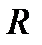 наудачу брошена точка. Найти вероятность того, что она не попадет в правильный треугольник, вписанный в этот круг. Решение. В этом случае мерой множества возможных исходов является площадь круга: наудачу брошена точка. Найти вероятность того, что она не попадет в правильный треугольник, вписанный в этот круг. Решение. В этом случае мерой множества возможных исходов является площадь круга: 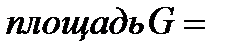 а мерой множества благоприятных исходов — разность площадей круга и треугольника (площадь треугольника, вписанного в круг - а мерой множества благоприятных исходов — разность площадей круга и треугольника (площадь треугольника, вписанного в круг - 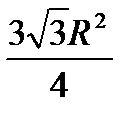 ): ): 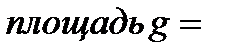 Вероятность заданного события равна Вероятность заданного события равна 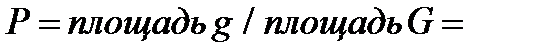 | |||||||||||||||||||||||||||||||
Задача 3.На отрезке 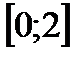 наудачу выбраны два числа наудачу выбраны два числа 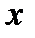 и и 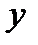 . Найти вероятность того, что эти числа удовлетворяют неравенствам . Найти вероятность того, что эти числа удовлетворяют неравенствам 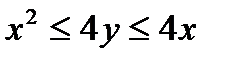 . .
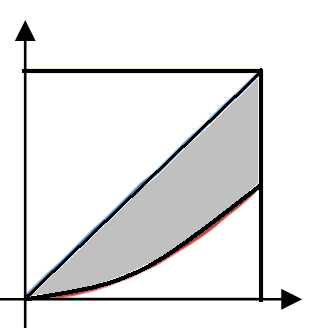
По условию задачи координаты точки Точки квадрата, координаты которых удовлетворяют неравенствам В этом случае мерой множества возможных исходов является площадь квадрата:
а мерой множества благоприятных исходов - площадь закрашенной фигуры:
Вероятность заданного события равна | |||||||||||||||||||||||||||||||
Задача 4.На отрезке 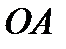 длины длины 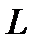 числовой оси числовой оси 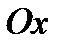 наудачу поставлены две точки: наудачу поставлены две точки: 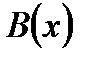 и и 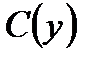 , причем , причем 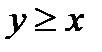 . Найти вероятность того, что длина отрезка . Найти вероятность того, что длина отрезка 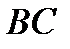 окажется меньше, чем окажется меньше, чем 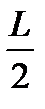 . Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси. Решение. . Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси. Решение.
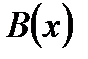 и и 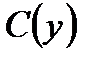 должны удовлетворять неравенствам должны удовлетворять неравенствам 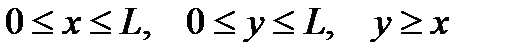 . . Введем в рассмотрение прямоугольную систему координат. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей заштрихованному прямоугольному треугольнику. Длина отрезка В этом случае мерой множества возможных исходов является площадь заштрихованного прямоугольного треугольника:
а мерой множества благоприятных исходов - площадь закрашенной трапеции:
Вероятность заданного события равна | |||||||||||||||||||||||||||||||
Задача 5. В шар вписан куб. Точка наудачу зафиксирована в шаре. Найти вероятность того, что точка попадет в куб. Решение. Введем обозначения 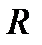 – радиус шара, – радиус шара, 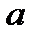 – ребро куба. В этом случае мерой множества возможных исходов является объем шара: – ребро куба. В этом случае мерой множества возможных исходов является объем шара: 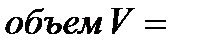 а мерой множества благоприятных исходов — объем вписанного круга: а мерой множества благоприятных исходов — объем вписанного круга: 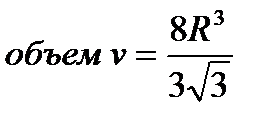 Вероятность заданного события равна Вероятность заданного события равна 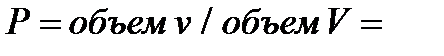 | |||||||||||||||||||||||||||||||
Задача 6. Какова вероятность того, что из трех взятых наудачу отрезков длины не больше 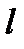 можно построить треугольник? Решение. Обозначим длины этих отрезков через можно построить треугольник? Решение. Обозначим длины этих отрезков через 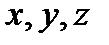 . Из условия задачи следует, что . Из условия задачи следует, что 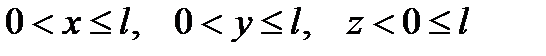 . Обозначим через . Обозначим через 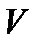 множество точек с координатами множество точек с координатами 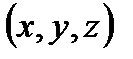 для которых выполняются данные неравенства, т. е. для которых выполняются данные неравенства, т. е. 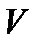 – куб с ребром – куб с ребром 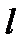 . .
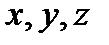 .Мы его отождествим с экспериментом, состоящим во взятии точки из куба .Мы его отождествим с экспериментом, состоящим во взятии точки из куба 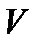 .Чтобы построить из этих трех отрезков треугольник, необходимо выполнение условий .Чтобы построить из этих трех отрезков треугольник, необходимо выполнение условий
Эти неравенства определяют тело Итак, в нашем случае мерой множества возможных исходов является объем куба с ребром
а мерой множества благоприятных исходов — объем тела
Вероятность заданного события равна | |||||||||||||||||||||||||||||||
| 3.2. Решить задачу | |||||||||||||||||||||||||||||||
| Задача 7. На отрезке длины 20 см помещен меньший отрезок длины 10 см. Найти вероятность того, что точка, поставленная на больший отрезок, попадет также и на меньший отрезок. Решение. | |||||||||||||||||||||||||||||||
Задача 8. Взяты наугад два положительных числа, каждое из которых не больше единицы. Какова вероятность того, что их сумма не превзойдет единицы, а произведение будет не больше 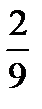 ?Решение. ?Решение. | |||||||||||||||||||||||||||||||
Задача 9. На отрезке 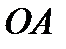 длины длины 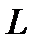 числовой оси числовой оси 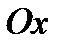 наудачу поставлены две точки: наудачу поставлены две точки: 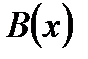 и и 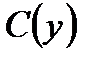 , причем , причем 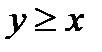 . Найти вероятность того, что длина отрезка . Найти вероятность того, что длина отрезка 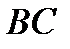 окажется меньше, длины отрезка окажется меньше, длины отрезка 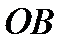 . Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси. Решение. . Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси. Решение. | |||||||||||||||||||||||||||||||
Основные теоремы

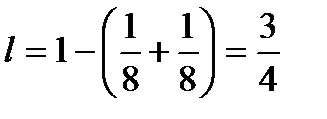 . Длина всего отрезка
. Длина всего отрезка 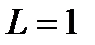 .
.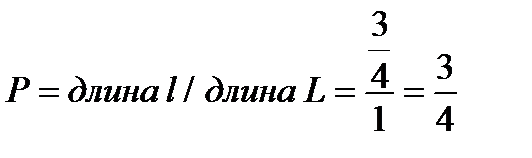 .
.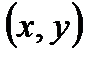 удовлетворяют системе неравенств
удовлетворяют системе неравенств 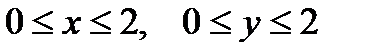 . Это означает, что точка
. Это означает, что точка 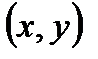 наудачу выбирается из множества точек квадрата, длина стороны которого равна 2.
наудачу выбирается из множества точек квадрата, длина стороны которого равна 2.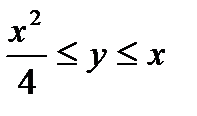 , принадлежат фигуре, закрашенной на рис.8.
, принадлежат фигуре, закрашенной на рис.8.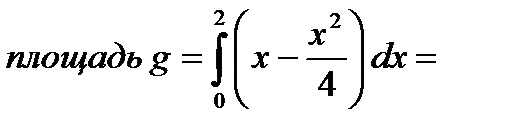
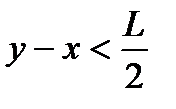 . Это неравенство выполняется для точек, которые лежат в закрашенной трапеции (рис.9).
. Это неравенство выполняется для точек, которые лежат в закрашенной трапеции (рис.9).
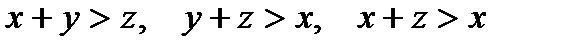 .
.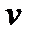 (рис.10), которое получается отбрасыванием от куба трех тетраэдров, отсекаемых плоскостями
(рис.10), которое получается отбрасыванием от куба трех тетраэдров, отсекаемых плоскостями 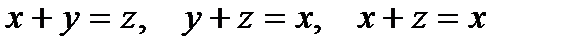 .
.