| 2.1. Сколько элементарных исходов благоприятствуют событию? а) Опыт: подбрасывание двух игральных кубиков. Событие – на обоих кубиках выпало одинаковое число очков. б) Опыт: из урны с пронумерованными от 1 до 30 карточками вытягивается одна. Событие – число на взятой карточке кратно 5. в) Опыт: из букв слова «дифференциал» наугад выбирается одна буква. Событие – извлеченная буква является гласной. г) Опыт: наблюдается время ожидания маршрутного такси пассажиром. Событие – время ожидания более двух минут. д) Опыт: выбирается наудачу точка внутри квадрата. Событие – выбранная точка попала в круг, вписанный в квадрат. Решение. |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 2.2. Разобрать решение задач, заполнив пропуски |
Задача1. В коробке находится 10 шаров. 3 красных, 2 зеленых, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым. Решение. Появление красного, зеленого или белого шаров составляют полную группу событий. Обозначим появление красного шара – событие 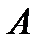 , появление зеленого – событие , появление зеленого – событие 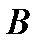 , появление белого – событие , появление белого – событие 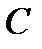 . Число исходов, благоприятствующих событию . Число исходов, благоприятствующих событию 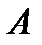 : : 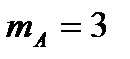 , событию , событию 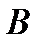 : : 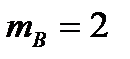 , событию , событию 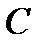 : : 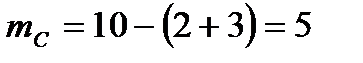 . А число всех исходов . А число всех исходов 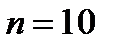 . Тогда в соответствии с формулами, получаем: . Тогда в соответствии с формулами, получаем: 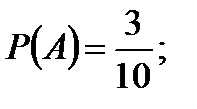 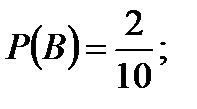 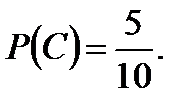 |
Задача 2.На четырех карточках написаны буквы «а», «б», «й», «т». Карточки перемешиваются и выкладываются в ряд. Найти вероятность того, что образовавшееся слово будет «байт». Решение. Обозначим появление слова «байт» событием 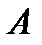 . В соответствии с комбинаторными принципами для определения общего числа элементарных исходов нужно подсчитать число упорядоченных наборов из четырех букв. Мы имеем дело с числом перестановок, поэтому число элементарных исходов . В соответствии с комбинаторными принципами для определения общего числа элементарных исходов нужно подсчитать число упорядоченных наборов из четырех букв. Мы имеем дело с числом перестановок, поэтому число элементарных исходов 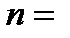 Слово «байт» образует только одна перестановка, то есть число благоприятных для события Слово «байт» образует только одна перестановка, то есть число благоприятных для события 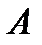 элементарных исходов элементарных исходов 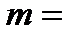 Поэтому Поэтому 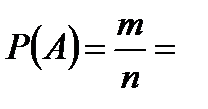 |
Задача 3. Из букв слова «ротор», составленного с помощью разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово «тор»? Решение. Обозначим появление слова «тор» событием 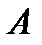 . Чтобы подсчитать количество исходов, благоприятствующих событию . Чтобы подсчитать количество исходов, благоприятствующих событию 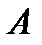 , одинаковые буквы снабдим номерами: «р1», «р2», «о1», «о2». Тогда слово «тор» получится в , одинаковые буквы снабдим номерами: «р1», «р2», «о1», «о2». Тогда слово «тор» получится в 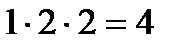 случаях («то1р1», «то1р2» , «то2р1», «то2р2»). Здесь мы пользуемся правилом произведения: букву «т» можно выбрать одним способом, букву «о» - двумя, букву «р» - двумя способами. случаях («то1р1», «то1р2» , «то2р1», «то2р2»). Здесь мы пользуемся правилом произведения: букву «т» можно выбрать одним способом, букву «о» - двумя, букву «р» - двумя способами. 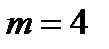 Общее число элементарных исходов равно: Общее число элементарных исходов равно: 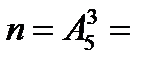 Тогда искомая вероятность Тогда искомая вероятность 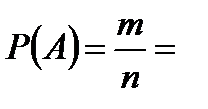 |
Задача 4.Даны 5 точек, никакие три из которых не лежат на одной прямой. Найти вероятность того, что, выбрав наугад две точки, учащийся получит нужную прямую. Решение. Пусть событие 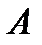 – выбор искомой прямой. Число всевозможных исходов равно количеству прямых, проходящих через заданные пять точек. Так как прямая определяется парой точек и порядок точек внутри этой пары не имеет значения, то каждая пара должна отличаться хотя бы одной точкой. Следовательно, нужно найти число сочетаний из пяти элементов по два, т.е. – выбор искомой прямой. Число всевозможных исходов равно количеству прямых, проходящих через заданные пять точек. Так как прямая определяется парой точек и порядок точек внутри этой пары не имеет значения, то каждая пара должна отличаться хотя бы одной точкой. Следовательно, нужно найти число сочетаний из пяти элементов по два, т.е. 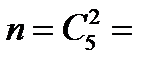 Искомой является только одна пара точек, значит число благоприятных для события Искомой является только одна пара точек, значит число благоприятных для события  элементарных исходов элементарных исходов  Поэтому Поэтому 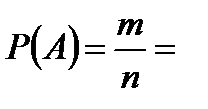 |
Задача 5.В первом ящике находится 15 бракованных и 10 годных деталей, которые тщательно перемешаны. Найти вероятность того, что а) извлеченная деталь годная (событие 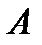 ); б) три извлеченные детали годные (событие ); б) три извлеченные детали годные (событие 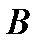 ); в) из трех извлеченных деталей две годные (событие ); в) из трех извлеченных деталей две годные (событие 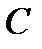 ). г) три извлеченные детали одного «достоинства» (событие ). г) три извлеченные детали одного «достоинства» (событие 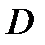 ) Решение. В этой задаче имеем дело с конечной схемой равновозможных исходов. Поэтому возможно применение классического определения вероятности. а) Число исходов, благоприятствующих событию ) Решение. В этой задаче имеем дело с конечной схемой равновозможных исходов. Поэтому возможно применение классического определения вероятности. а) Число исходов, благоприятствующих событию 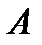 : : 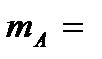 А число всех исходов: А число всех исходов: 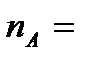 Поэтому Поэтому 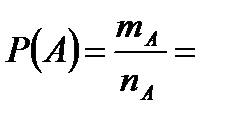 Выбор трех деталей из 25 можно осуществить Выбор трех деталей из 25 можно осуществить 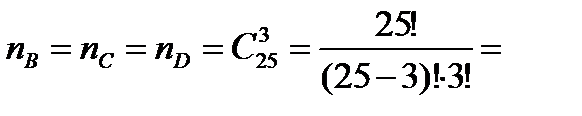 способами. б) Извлечь три годные детали возможно способами. б) Извлечь три годные детали возможно 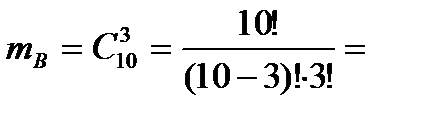 способами. Тогда способами. Тогда 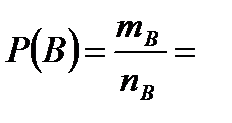 в) Извлечь две годные детали и одну бракованную деталь возможно (по основному правилу комбинаторики – правилу умножения) в) Извлечь две годные детали и одну бракованную деталь возможно (по основному правилу комбинаторики – правилу умножения) 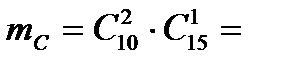 способами. Тогда способами. Тогда 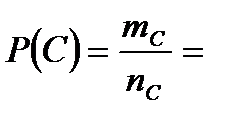 г) Событие г) Событие  означает, что извлеченные детали либо годные, либо бракованные. Значит, по основному правилу комбинаторики – правилу сложения получаем, что общее число случаев, благоприятствующих событию означает, что извлеченные детали либо годные, либо бракованные. Значит, по основному правилу комбинаторики – правилу сложения получаем, что общее число случаев, благоприятствующих событию  равно равно 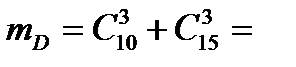 Тогда Тогда 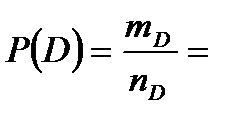 |
Замечание.Задачу 5в можно решить, используя урновую схему: в урне имеется 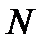 шаров, из них шаров, из них 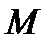 первого вида, первого вида, 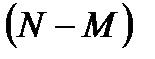 второго вида. Из данной урны извлекается второго вида. Из данной урны извлекается 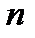 шаров. Требуется определить вероятность того, что в выборке объема шаров. Требуется определить вероятность того, что в выборке объема 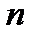 будет обнаружено будет обнаружено 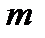 шаров первого вида и шаров первого вида и 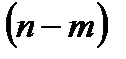 второго. Обозначив через событие второго. Обозначив через событие 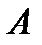 «в выборке объема «в выборке объема 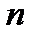 имеется имеется 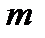 шаров первого вида и шаров первого вида и 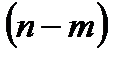 второго», получим что, второго», получим что, 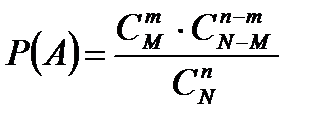 . Знаменатель этой дроби представляет собой число возможных исходов опыта, то есть количество различных наборов по . Знаменатель этой дроби представляет собой число возможных исходов опыта, то есть количество различных наборов по 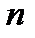 элементов, выбранных из элементов, выбранных из 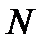 имеющихся без учета их качественного состава. В числителе — число благоприятных исходов, представляющее собой число возможных наборов из имеющихся без учета их качественного состава. В числителе — число благоприятных исходов, представляющее собой число возможных наборов из 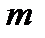 элементов нужного вида, умноженное на количество возможных наборов из элементов нужного вида, умноженное на количество возможных наборов из 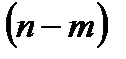 предметов второго типа. предметов второго типа. |
Задача 6. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг. Решение. Событие 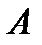 – появление бракованных книг. Из условия задачи число испытаний, в которых наступило событие равно – появление бракованных книг. Из условия задачи число испытаний, в которых наступило событие равно 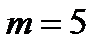 . А общее количество испытаний – . А общее количество испытаний – 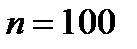 . Тогда относительная частота события . Тогда относительная частота события 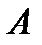 определяется равенством определяется равенством 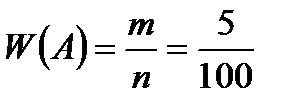 . . |
| 2.3. Решить задачу |
| Задача 7. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры. |
| Решение. |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| Задача 8. Имеется пять отрезков, длины которых соответственно равны: 1, 3, 5, 7, 9 см. Определить вероятность того, что с помощью взятых наудачу трех отрезков можно построить треугольник. |
| Решение. |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| Задача9.При стрельбе по мишени частота попаданий 0,75. Найти число попаданий при 40 выстрелах. Решение. |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| Задача10.На отрезке натурального ряда от 1 до 20 найти частоту простых чисел. Решение. |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
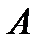 , появление зеленого – событие
, появление зеленого – событие 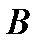 , появление белого – событие
, появление белого – событие 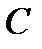 . Число исходов, благоприятствующих событию
. Число исходов, благоприятствующих событию 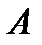 :
: 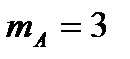 , событию
, событию 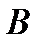 :
: 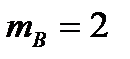 , событию
, событию 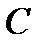 :
: 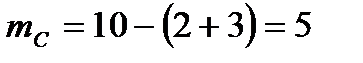 . А число всех исходов
. А число всех исходов 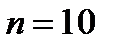 . Тогда в соответствии с формулами, получаем:
. Тогда в соответствии с формулами, получаем: 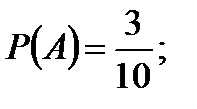
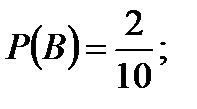
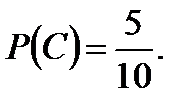
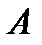 . В соответствии с комбинаторными принципами для определения общего числа элементарных исходов нужно подсчитать число упорядоченных наборов из четырех букв. Мы имеем дело с числом перестановок, поэтому число элементарных исходов
. В соответствии с комбинаторными принципами для определения общего числа элементарных исходов нужно подсчитать число упорядоченных наборов из четырех букв. Мы имеем дело с числом перестановок, поэтому число элементарных исходов 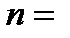 Слово «байт» образует только одна перестановка, то есть число благоприятных для события
Слово «байт» образует только одна перестановка, то есть число благоприятных для события 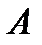 элементарных исходов
элементарных исходов 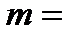 Поэтому
Поэтому 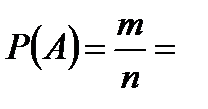
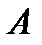 . Чтобы подсчитать количество исходов, благоприятствующих событию
. Чтобы подсчитать количество исходов, благоприятствующих событию 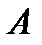 , одинаковые буквы снабдим номерами: «р1», «р2», «о1», «о2». Тогда слово «тор» получится в
, одинаковые буквы снабдим номерами: «р1», «р2», «о1», «о2». Тогда слово «тор» получится в 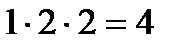 случаях («то1р1», «то1р2» , «то2р1», «то2р2»). Здесь мы пользуемся правилом произведения: букву «т» можно выбрать одним способом, букву «о» - двумя, букву «р» - двумя способами.
случаях («то1р1», «то1р2» , «то2р1», «то2р2»). Здесь мы пользуемся правилом произведения: букву «т» можно выбрать одним способом, букву «о» - двумя, букву «р» - двумя способами. 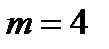 Общее число элементарных исходов равно:
Общее число элементарных исходов равно: 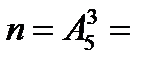 Тогда искомая вероятность
Тогда искомая вероятность 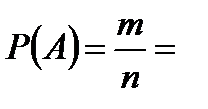
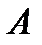 – выбор искомой прямой. Число всевозможных исходов равно количеству прямых, проходящих через заданные пять точек. Так как прямая определяется парой точек и порядок точек внутри этой пары не имеет значения, то каждая пара должна отличаться хотя бы одной точкой. Следовательно, нужно найти число сочетаний из пяти элементов по два, т.е.
– выбор искомой прямой. Число всевозможных исходов равно количеству прямых, проходящих через заданные пять точек. Так как прямая определяется парой точек и порядок точек внутри этой пары не имеет значения, то каждая пара должна отличаться хотя бы одной точкой. Следовательно, нужно найти число сочетаний из пяти элементов по два, т.е. 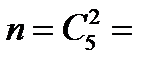 Искомой является только одна пара точек, значит число благоприятных для события
Искомой является только одна пара точек, значит число благоприятных для события 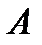 элементарных исходов
элементарных исходов 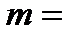 Поэтому
Поэтому 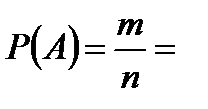
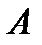 ); б) три извлеченные детали годные (событие
); б) три извлеченные детали годные (событие 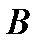 ); в) из трех извлеченных деталей две годные (событие
); в) из трех извлеченных деталей две годные (событие 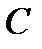 ). г) три извлеченные детали одного «достоинства» (событие
). г) три извлеченные детали одного «достоинства» (событие 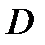 ) Решение. В этой задаче имеем дело с конечной схемой равновозможных исходов. Поэтому возможно применение классического определения вероятности. а) Число исходов, благоприятствующих событию
) Решение. В этой задаче имеем дело с конечной схемой равновозможных исходов. Поэтому возможно применение классического определения вероятности. а) Число исходов, благоприятствующих событию 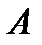 :
: 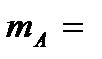 А число всех исходов:
А число всех исходов: 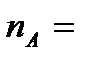 Поэтому
Поэтому 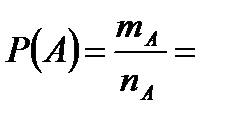 Выбор трех деталей из 25 можно осуществить
Выбор трех деталей из 25 можно осуществить 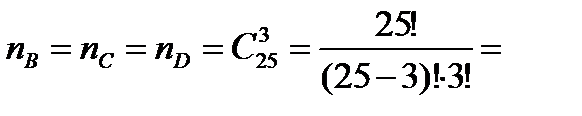 способами. б) Извлечь три годные детали возможно
способами. б) Извлечь три годные детали возможно 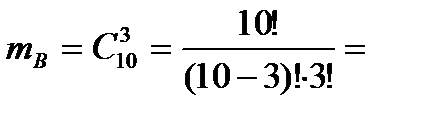 способами. Тогда
способами. Тогда 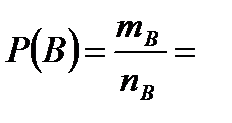 в) Извлечь две годные детали и одну бракованную деталь возможно (по основному правилу комбинаторики – правилу умножения)
в) Извлечь две годные детали и одну бракованную деталь возможно (по основному правилу комбинаторики – правилу умножения) 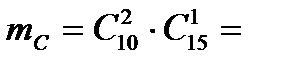 способами. Тогда
способами. Тогда 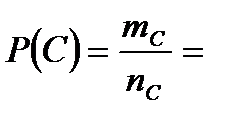 г) Событие
г) Событие 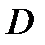 означает, что извлеченные детали либо годные, либо бракованные. Значит, по основному правилу комбинаторики – правилу сложения получаем, что общее число случаев, благоприятствующих событию
означает, что извлеченные детали либо годные, либо бракованные. Значит, по основному правилу комбинаторики – правилу сложения получаем, что общее число случаев, благоприятствующих событию 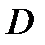 равно
равно 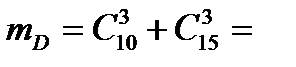 Тогда
Тогда 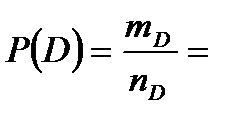
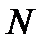 шаров, из них
шаров, из них 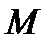 первого вида,
первого вида, 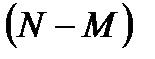 второго вида. Из данной урны извлекается
второго вида. Из данной урны извлекается 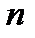 шаров. Требуется определить вероятность того, что в выборке объема
шаров. Требуется определить вероятность того, что в выборке объема 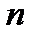 будет обнаружено
будет обнаружено 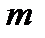 шаров первого вида и
шаров первого вида и 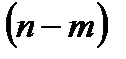 второго. Обозначив через событие
второго. Обозначив через событие 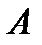 «в выборке объема
«в выборке объема 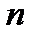 имеется
имеется 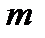 шаров первого вида и
шаров первого вида и 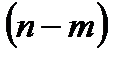 второго», получим что,
второго», получим что, 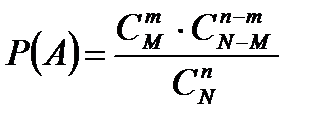 . Знаменатель этой дроби представляет собой число возможных исходов опыта, то есть количество различных наборов по
. Знаменатель этой дроби представляет собой число возможных исходов опыта, то есть количество различных наборов по 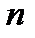 элементов, выбранных из
элементов, выбранных из 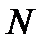 имеющихся без учета их качественного состава. В числителе — число благоприятных исходов, представляющее собой число возможных наборов из
имеющихся без учета их качественного состава. В числителе — число благоприятных исходов, представляющее собой число возможных наборов из 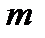 элементов нужного вида, умноженное на количество возможных наборов из
элементов нужного вида, умноженное на количество возможных наборов из 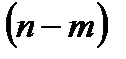 предметов второго типа.
предметов второго типа. 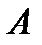 – появление бракованных книг. Из условия задачи число испытаний, в которых наступило событие равно
– появление бракованных книг. Из условия задачи число испытаний, в которых наступило событие равно 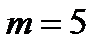 . А общее количество испытаний –
. А общее количество испытаний – 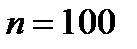 . Тогда относительная частота события
. Тогда относительная частота события 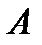 определяется равенством
определяется равенством 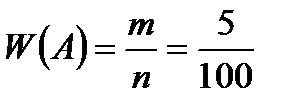 .
. 