Вероятностью события 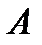 называется математическая оценка возможности появления этого события в результате опыта. называется математическая оценка возможности появления этого события в результате опыта. |
| 1.1. Записать формулу нахождения относительной частоты |
| формула | определение |
| | Относительная частота появления события в серии опытов со случайными исходами – отношение числа опытов, в которых произошло событие, к числу всех опытов. |
1.2. Записать формулу нахождения статистической вероятности события 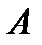 |
| формула | определение |
| | Статистической вероятность события – постоянное число, около которого группируются относительные частоты при увеличении числа опытов. |
| 1.3. Записать формулу нахождения вероятности события по классическому определению |
| формула | определение |
| | Классическое определение вероятности события: отношение числа исходов, благоприятствующих появлению события, к числу всех равновозможных исходов. |
| 1.4. Записать формулу нахождения геометрической вероятности |
| формула | определение |
| 1) Линейный случай | Пусть отрезок 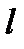 составляет часть отрезка составляет часть отрезка 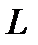 . На отрезок . На отрезок 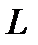 наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка 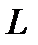 , вероятность попадания точки на отрезок , вероятность попадания точки на отрезок 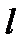 пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка 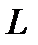 . . |
| 2) Плоский случай | Пусть плоская фигура 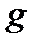 составляет часть плоской фигуры составляет часть плоской фигуры 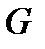 . На фигуру . На фигуру 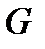 наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры 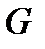 , вероятность попадания брошенной точки на фигуру , вероятность попадания брошенной точки на фигуру 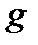 пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно 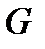 , ни от формы , ни от формы 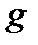 . . |
| 3) Пространственный случай | Пусть пространственное тело 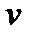 составляет часть пространственного тела составляет часть пространственного тела 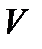 . В тело . В тело 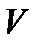 наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке тела наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке тела 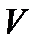 , вероятность попадания брошенной точки в тело , вероятность попадания брошенной точки в тело 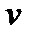 пропорциональна объему этого тела и не зависит ни от ее расположения относительно пропорциональна объему этого тела и не зависит ни от ее расположения относительно 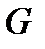 , ни от формы , ни от формы 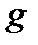 . . |
| 4) Общий случай | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | | | |
| Замечание. В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю): справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным. |
Наши рекомендации
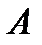 называется математическая оценка возможности появления этого события в результате опыта.
называется математическая оценка возможности появления этого события в результате опыта. 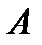
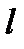 составляет часть отрезка
составляет часть отрезка 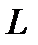 . На отрезок
. На отрезок 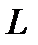 наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка
наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка 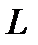 , вероятность попадания точки на отрезок
, вероятность попадания точки на отрезок 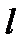 пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка
пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка 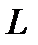 .
. 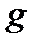 составляет часть плоской фигуры
составляет часть плоской фигуры 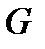 . На фигуру
. На фигуру 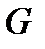 наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры
наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры 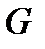 , вероятность попадания брошенной точки на фигуру
, вероятность попадания брошенной точки на фигуру 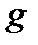 пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно
пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно 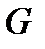 , ни от формы
, ни от формы 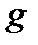 .
. 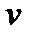 составляет часть пространственного тела
составляет часть пространственного тела 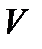 . В тело
. В тело 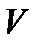 наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке тела
наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке тела 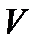 , вероятность попадания брошенной точки в тело
, вероятность попадания брошенной точки в тело 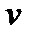 пропорциональна объему этого тела и не зависит ни от ее расположения относительно
пропорциональна объему этого тела и не зависит ни от ее расположения относительно 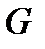 , ни от формы
, ни от формы 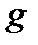 .
. 