Точечные и интервальные оценки
Смоленск 2009
Оценки параметров генеральной совокупности, полученные на основании выборки, называются статистическими. Если статистическая оценка характеризуется одним числом, она называется точечной.
Выборочная средняя определяется как среднее арифметическое полученных по выборке значений:
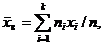
Для устранения смещённости выборочной дисперсии её умножают на величину n /(n - 1) и получают
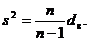
Величину 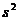 называют несмещенной или «исправленной» выборочной дисперсией.
называют несмещенной или «исправленной» выборочной дисперсией.
В некоторых случаях для удобства расчётов при определении статистических оценок переходят к условным вариантам. Например, если варианты 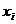 - большие числа, то используют разности
- большие числа, то используют разности
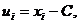
где С – произвольно выбранное число (ложный нуль), такое, при котором условные варианты принимают небольшие значения.
В этом случае
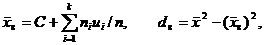
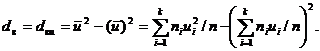
Для изменения значения варианты можно ввести также условные варианты путём использования масштабного множителя:
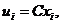
где 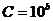 (b выбирается положительным или отрицательным целым числом).
(b выбирается положительным или отрицательным целым числом).
Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.
Метод наибольшего правдоподобия, применяемый для определения точечной оценки, опирается на использование условий экстремума функций одной или нескольких случайных величин. В качестве такой функции принимают функцию правдоподобия.
Для дискретной случайной величины функция правдоподобия принимает вид
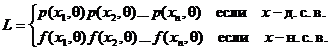
где 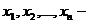 варианты выборки;
варианты выборки;
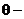 параметр, для которого находится оценка;
параметр, для которого находится оценка;
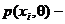 вероятность события X = xi, зависящая от параметра
вероятность события X = xi, зависящая от параметра 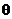 ;
;
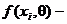 заданная функция плотности вероятности в точках xi..
заданная функция плотности вероятности в точках xi..
Так как функции L и lnL достигают максимума при одном и том же значении 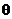 , то обычно точки экстремума находятся для lnL. Для этого определяется производная
, то обычно точки экстремума находятся для lnL. Для этого определяется производная 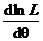 и приравнивается к нулю.
и приравнивается к нулю.
Если статистическая оценка параметров закона распределения случайной величины Х характеризуется двумя числами – концами интервала, то такая оценка называется интервальной.
Интервал, в который попадает оцениваемый параметр с заданной надёжностью (вероятностью), называется доверительным. Доверительный интервал применяется в случае сравнительно небольшого объёма выборки, когда предполагается, что надёжность точечной оценки может быть невысокой.
Доверительный интервал для оценки математического ожидания случайной величины Х с заданной надёжностью γ в случае нормального закона распределения определяется на основе неравенств
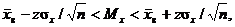
где z – значение аргумента функции Лапласа, получаемое из
таблицы (см. Приложение), с учётом того, что 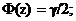
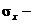 известное среднее квадратичное отклонение или его
известное среднее квадратичное отклонение или его
оценка;
n – объём выборки.
Доверительный интервал для оценки среднего квадратичного отклонения случайной величины X с надёжностью γ для нормального закона распределения случайной величины находится из неравенств
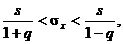
где s – несмещённое значение выборочного среднего квадра-
тичного отклонения;
q – параметр, который находится по таблице (см. Приложение) на основе известного значения объёма выборки n и заданной надёжности оценки γ.
Цель занятия: 1. Добиться усвоения простейших навыков построения точечных и интервальных оценок. Обратить внимание студентов на случайный характер получаемых оценок, на проявление закона больших чисел, если наблюдений много.
2. Закрепить в сознании студентов соответствие между понятиями прикладной и математической статистики:
В задачах 5 и 6 четко провести разграничение методов построения доверительного интервала.
К занятию по данной теме должны быть подготовлены ответы на следующие вопросы:
1. В чем заключается сущность задачи нахождения точечных оценок неизвестных параметров распределения?
2. Что называется доверительным интервалом? доверительной вероятностью?
3. Что называется предельной погрешностью точечной оценки параметра?
4. Что происходит с длиной доверительного интервала при увеличении объема выборки? увеличении доверительной вероятности?
5. Являются ли концы интервалов постоянными величинами? Случайными величинами?
Задача 1. В итоге 8 измерений некоторой физической величины одним и тем же прибором получены следующие результаты: x1=50,3; x2=50,1; x3=50,4; x4=49,9; x5=50,0; x6=50,2; x7=50,8; x8=50,7. В предположении, что систематическая ошибка отсутствует, найти оценку измеряемой величины и оценку дисперсии ошибки прибора.
Решение. Результаты измерений Х можно представить в виде Х = a+Y, где a – измеряемая физическая величина, а Y – ошибка измерения. Из предположения об отсутствии систематической ошибки следует, что M(Y) = 0 и M(X)=M(a)+M(Y)=a. Поэтому для оценки a можно использовать оценку математического ожидания, т.е. среднее арифметическое
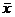 =
= 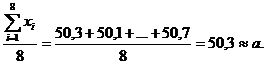
Так как D(X)=D(a)+D(Y)=D(Y), представление об ошибке прибора дает несмещенная оценка дисперсии.
Задача 2. В табл.4 приведены сгруппированные данные измерений роста у 50 случайно отобранных студентов.
Таблица 4.
| Рост студентов, см | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 | 182-186 |
| Число студентов |
Оценить средний рост и дисперсию роста студентов.
Решение. Так как данные сгруппированы, то в качестве представителя каждой группы можно взять середину интервала. Тогда
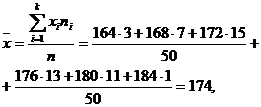
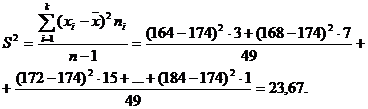
S = 4,87.
Задача 3. Известно, что число независимых опытов до первого появления события имеет геометрический закон распределения:
| X | 1 | 2 | 3 | … | k | … |
| P | P | qp | q2p | … | qk-1p | … |
где p – неизвестный параметр, который равен вероятности появления события в одном опыте, q = 1 – p. Проделано 5 серий опытов до первого появления события. Они дали следующие результаты: x1=10, x2=4, x3=2, x4=11, x5=3. Найти оценку наибольшего правдоподобия для р. Оценить р по методу моментов.
Решение.Найдем функцию правдоподобия в общем случае
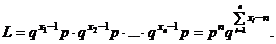
Тогда
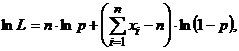
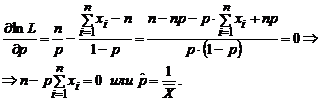
В нашем случае 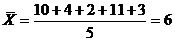 .Значит
.Значит 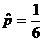 . По методу моментов получается та же оценка, так как
. По методу моментов получается та же оценка, так как 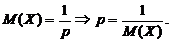 А оценкой
А оценкой 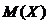 является
является 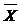 .
.
Задача 4. Для обследования крупной парии изделий отобрано наугад 900 штук. Проверка показала, что среди них 810стандартны. Построить доверительный интервал для доли стандартных изделий в партии. Уровень надёжности выбрать равным 0,95.
Решение.Пусть доля стандартных изделий в партии равна p. Оценкой её может служить величина 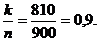 По таблице функции Лапласа
По таблице функции Лапласа 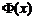 находим такое
находим такое 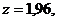 чтобы
чтобы 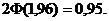 Тогда по формуле
Тогда по формуле
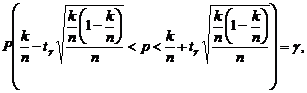
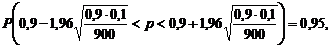
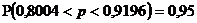 .
.
Задача 5. По данным задачи 2, построить доверительный интервал для среднего роста студентов с надёжностью 0,9.
Решение.По таблице функции 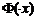 находим значение
находим значение 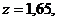 для которого
для которого 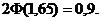 Тогда по формуле
Тогда по формуле
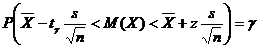
находим
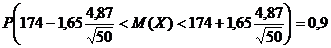
или
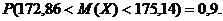
Задача 6.Измерения сопротивления резистора дали следующие результаты (в омах)
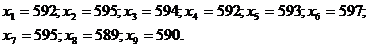
Известно, что ошибки измерения имеют нормальный закон распределения. Систематическая ошибка отсутствует. Построить доверительный интервал для истинного сопротивления резистора с надёжностью 0,99 в предположении:
а) дисперсия ошибки измерения известна и равна 4;
б) в предположении неизвестной ошибки измерения.
Решение.Результаты измерения 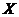 можно представить в виде X = a + Y, где a - истинное значение измеряемой величины, а Y - ошибка измерения. Систематическая ошибка отсутствует (M(Y)=0), поэтому M(X)=M(a)+M(Y)=a и D(X)=D(a)+D(Y)=D(Y), т.е. доверительный интервал для M(X) будет доверительным интервалом для истинного значения сопротивления резистора. В данной серии наблюдений
можно представить в виде X = a + Y, где a - истинное значение измеряемой величины, а Y - ошибка измерения. Систематическая ошибка отсутствует (M(Y)=0), поэтому M(X)=M(a)+M(Y)=a и D(X)=D(a)+D(Y)=D(Y), т.е. доверительный интервал для M(X) будет доверительным интервалом для истинного значения сопротивления резистора. В данной серии наблюдений
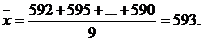
Если дисперсия известна, то доверительный интервал можно построить, используя устойчивость нормального закона распределения. Так как 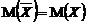 и
и 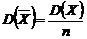 ,
,
то 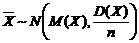 , откуда
, откуда
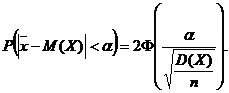
Из таблицы функции Лапласа 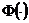 находим, что
находим, что 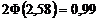 . Тогда
. Тогда 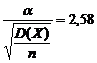 или
или 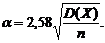
В результате
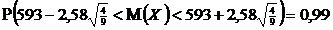
или
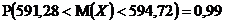 .
.
В случае неизвестной дисперсии, её оценку можно получить на основе тех же опытных данных
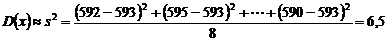
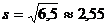 .
.
По таблице распределения Стьюдента для 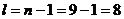 степеней свободы и заданной вероятности
степеней свободы и заданной вероятности 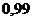 находим такое
находим такое 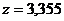 , что
, что
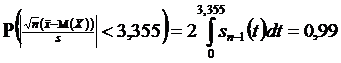 .
.
Отсюда
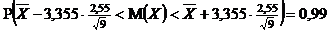 ,
,
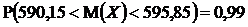 .
.
Задача 7. По данным выборки объёма n = 25 найдено несмещённое значение выборочного среднего квадратичного отклонения s = 3 нормально распределённой случайной величины Х. Найти с надёжностью 0,99 доверительный интервал для оценки среднего квадратичного отклонения случайной величины.
Решение. На основании данных значений γ= 0,99, n = 25 по таблице (см. Приложение) находим значение q = 0,49. Подставляем в неравенства
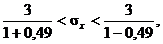
откуда
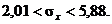
Задача 8. На основании выборочных наблюдений производительности труда 20 работниц было установлено, что среднее квадратическое отклонение суточной выработки составляет 15 м ткани в час. Предполагая, что производительность труда работницы имеет нормальное распределение, найти границы, в которых с надёжностью 0,9 заключены генеральные дисперсия и среднее квадратическое отклонение суточной выработки работниц.
Решение. Имеем γ = 0,9; (1 – γ)/2 = 0,05. (1+ γ)/2 = 0,95.
При числе степени свободы k = n – 1 = 20 – 1 = 19 определим 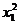 и
и 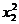 по таблице (см. Приложение) для вероятностей 0,95 и 0,05, т.е.
по таблице (см. Приложение) для вероятностей 0,95 и 0,05, т.е. 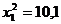 и
и 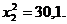 Тогда доверительный интервал для
Тогда доверительный интервал для 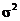 можно записать в виде:
можно записать в виде:
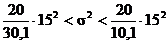 или
или 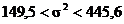 и для
и для 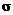 :
: 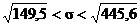 или
или 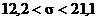 (м/ч).
(м/ч).
Итак, с надёжностью 0,9 дисперсия суточной выработки работниц заключена в границах от 149,5 до 445,6, а её среднее квадратическое отклонение – от 12,2 до 21,1 метров ткани в час.
Дополнительные задачи.
Задача 1.Найти несмещённую и состоятельную оценку доли рабочих цеха с выработкой не менее 124% по выборке, представленной в таблице 1 (предыдущего урока).
Решение. Несмещенной и состоятельной оценкой генеральной доли 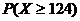 является выборочная доля
является выборочная доля
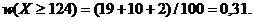
Задача 2.Найти выборочную среднюю по данному распределению выборки:
| xi | |||
| ni |
Решение. Так как выборочные значения – большие числа, то целесообразно ввести условные варианты. В качестве ложного нуля выбираем С = 1470 и рассчитываем ui по формуле 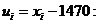
| xi | -20 | ||
| ni |
Определяем выборочную среднюю: 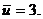
После этого находим 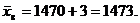
Задача 3.Найти выборочную дисперсию по данному распределению выборки:
| xi | 0,02 | 0,05 | 0,08 |
| ni |
Решение. В целях упрощения расчётов целесообразно перейти к условным вариантам 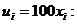
| xi | |||
| ni |
Найдём выборочную дисперсию условных вариант:
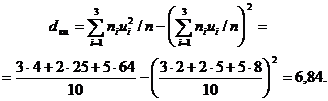
Выборочная дисперсия данного распределения вариант xi находится на основе выражения
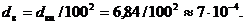
Задача 4. На предприятии изготавливается определённый вид продукции. Ежемесячный объём выпуска этой продукции является случайной величиной, для характеристики которой принят показательный закон распределения
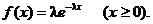
В течение шести месяцев проводился замер объёмов выпуска продукции, получены следующие данные:
| Месяц | ||||||
| Объём выпуска |
Найти оценку параметра λ.
Решение. Так как закон распределения содержит лишь один параметр λ, то для его оценки требуется составить одно уравнение.
Находим выборочную среднюю:
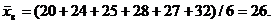
Определяем математическое ожидание:
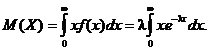
Интегрируя по частям, получаем
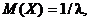
откуда
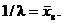
Полученное равенство является приближённым, так как правая часть его является случайной величиной. Таким образом, из уравнения получается не точное значение λ , а его оценка 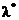 :
:
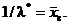
Итак, 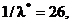 откуда
откуда 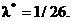
Задача 5. Случайная величина Х (время безотказной работы элемента) имеет показательное распределение 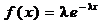
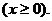 Ниже приведено эмпирическое распределение среднего времени работы 1000 элементов (в первой строке указано среднее время xi безотказной работы одного элемента в часах; во второй строке указана частота ni – количество элементов, проработавших в среднем xi часов):
Ниже приведено эмпирическое распределение среднего времени работы 1000 элементов (в первой строке указано среднее время xi безотказной работы одного элемента в часах; во второй строке указана частота ni – количество элементов, проработавших в среднем xi часов):
| xi | |||||||
| ni |
Найти методом наибольшего правдоподобия точечную оценку неизвестного параметра λ показательного распределения.
Решение. Составим функцию правдоподобия
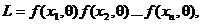
учитывая, что 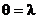 и, следовательно,
и, следовательно, 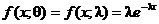
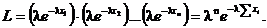
Найдём логарифмическую функцию правдоподобия:
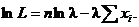
Найдём первую производную по λ:
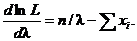
Запишем уравнение правдоподобия, для чего приравняем первую производную к нулю: 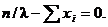 Найдём критическую точку, для чего решим полученное уравнение относительно λ:
Найдём критическую точку, для чего решим полученное уравнение относительно λ:
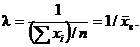
Найдём вторую производную по λ:
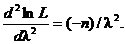
Легко видеть, что при 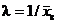 вторая производная отрицательна; следовательно, это точка есть точка максимума и, значит, в качестве оценки наибольшего правдоподобия надо принять величину, обратную выборочной средней:
вторая производная отрицательна; следовательно, это точка есть точка максимума и, значит, в качестве оценки наибольшего правдоподобия надо принять величину, обратную выборочной средней: 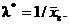
Так как
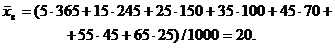
то
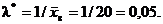
Домашнее задание.
Задача 1. Выручка в магазине от продажи обуви составила соответственно по месяцам следующие значения (млн. руб.):
| Месяц | ||||||||||||
| P | 0,2 | 0,5 | 0,4 | 0,2 | 0,4 | 0,5 | 0,2 | 0,2 | 0,4 | 0,5 | 0,4 | 0,2 |
Найти выборочную среднюю и выборочную дисперсию.
Задача 2. При условии показательного распределения случайной величины X
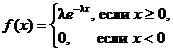
произведена выборка
| xi | |||||
| ni |
Найти оценку параметра λ методом моментов.
Задача 3. Стеклянные однородные изделия отправлены для реализации из Москвы в Новосибирск в 1000 контейнерах. После поступления товара было выявлено количество разбитых изделий в каждом контейнере. Результаты представлены в таблице:
| xi | |||||
| ni |
Считая, что число разбитых изделий описывается законом Пуассона, найти точечную оценку параметра λ .
Задача 4. Найти доверительный интервал с надёжностью 0,8 для оценки математического ожидания нормально распределённой случайной величины Х со средним квадратичным отклонением 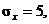 выборочной средней
выборочной средней 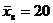 и объёмом выборки n = 25.
и объёмом выборки n = 25.
Задача 5. В нескольких мелких магазинах проведена проверка качества 100 изделий, после чего осуществлена обработка полученных данных. В результате получено несмещённое значение выборочного среднего квадратичного отклонения s = 4. Считая распределение качественных изделий нормальным, найти с надёжностью 0,95 доверительный интервал для оценки среднего квадратичного отклонения.
Ответы: 1) 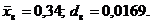 2)
2) 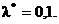 3)
3) 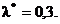 4) (18,72; 21,28). 5) (3,5; 4,67).
4) (18,72; 21,28). 5) (3,5; 4,67).
СМОЛЕНСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
Г. С. ЕВДОКИМОВА
ПРАКТИКУМ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
МОДУЛЬ 9–10
Проверка статистических гипотез. Критерий χ2
Смоленск 2009
Если принятое решение о законе распределения генеральной совокупности или о числовых значениях его параметров проверяется по выборочным данным, то говорят о проверке статистических гипотез. Проверке подвергается гипотеза об отсутствии разности между принятым и найденным по выборке значениями исследуемого параметра. Такую гипотезу называют нулевой. Противоположную ей гипотезу называют альтернативной.
Схема проверки нулевой гипотезы:
1. Рассматривая выборочные данные x1, x2 ,...,xn и учитывая конкретные условия задачи, принимают H0 – нулевую гипотезу и H1 – альтернативную гипотезу, конкурирующую с Н0.
2. Так как решение о справедливости гипотезы Н0 принимается на основе выборочных данных, могут возникать ошибки двух родов:
– гипотеза Н0 отвергается, а на самом деле она верна – это ошибка первого рода; вероятность ошибки первого рода равна уровню значимости α , т.е. 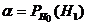 ;
;
– гипотеза Н0 принимается, а на самом деле она неверна – это ошибка второго рода; вероятность ошибки второго рода равна β, т.е. 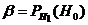 .
.
Соответственно, вероятность принять первую верную гипотезу равна 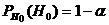 , а вероятность отвергнуть неверную гипотезу Н0 равна
, а вероятность отвергнуть неверную гипотезу Н0 равна 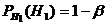 .
.
3. Используя выборочные данные, вводят статистический критерий – некоторую функцию К, зависящую от условий решаемой статистической задачи. Эти функции, являясь случайными величинами, подчинены некоторому известному, затабулированному закону распределения (t-распределение, χ2-распределение или нормальное распределение).
4. В зависимости от принятого уровня значимости из области допустимых значений функции критерия К выделяют критическую область ω. Далее руководствуются следующим правилом: если вычисленное по выборке значение критерия К попадает в критическую область, то Н0 отвергается и принимается гипотеза Н1. При этом возможно, что Н0 справедлива и, следовательно, совершена ошибка первого рода, вероятность которой α, т.е. 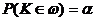 .
.
Возможны три варианта расположения критической области:
правосторонняя критическая область, состоящая из интервала 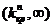 , где
, где 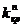 определяется из условия
определяется из условия 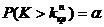 ;
;
левосторонняя критическая область, состоящая из интервала 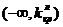 , где
, где 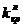 определяется из условия
определяется из условия 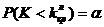 ;
;
двусторонняя критическая область, состоящая из интервалов 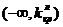 и
и 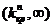 , где точки
, где точки 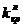 и
и 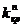 определяются из условий
определяются из условий 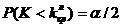 и
и 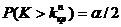 .
.
5. По выборочным данным находят числовое значение критерия (kr). Если kr попадает в критическую область ω, то гипотеза Н0 отвергается и принимается альтернативная гипотеза Н1. Если kr не попадает в критическую область, то гипотеза Н0 принимается.
При проверке статистических гипотез учитываются конкретные условия рассматриваемой задачи.
На практике часто требуется оценить, соответствуют ли действительности рекламные данные о параметрах того или иного товара. В этом случае возникает задача сравнения выборочной средней с анонсируемым значением этого параметра.
Задача 1. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 2900 ч. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 ч при выборочном среднем квадратичном отклонении 700 ч. При 5%-м уровне значимости проверить гипотезу о том, что значение 2900 ч является математическим ожиданием.
Решение. Предположим, что случайная величина срока безотказной работы подчинена нормальному закону распределения. Требуется проверить гипотезу о числовом значении математического ожидания нормально распределенной величины (генеральной средней) при неизвестной генеральной дисперсии. В этом случае в качестве критерия выбирают функцию
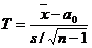 ,
,
где 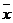 – выборочная средняя, а0 – математическое ожидание, s – выборочное среднее квадратичное отклонение. Случайная величина Т имеет t-распределение (распределение Стьюдента) с
– выборочная средняя, а0 – математическое ожидание, s – выборочное среднее квадратичное отклонение. Случайная величина Т имеет t-распределение (распределение Стьюдента) с 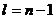 степенями свободы.В данной задаче речь идет о сравнении выборочной средней 2720 ч с гипотетическим математическим ожиданием
степенями свободы.В данной задаче речь идет о сравнении выборочной средней 2720 ч с гипотетическим математическим ожиданием 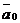 =2900 ч, при этом выборочное среднее квадратичное отклонение равно 700 ч.
=2900 ч, при этом выборочное среднее квадратичное отклонение равно 700 ч.
Требуется найти критическую область для нулевой гипотезы Н0: а0=2900 при альтернативной гипотезе Н1: а1<2900. Очевидно, что другие альтернативные гипотезы ( 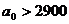 и
и 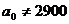 ) нецелесообразны, т.к. потребитель обычно обеспокоен лишь тем, что срок службы изделия может оказаться меньше гарантируемого поставщиком.
) нецелесообразны, т.к. потребитель обычно обеспокоен лишь тем, что срок службы изделия может оказаться меньше гарантируемого поставщиком.
Критическая область левосторонняя; 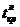 находим из условия
находим из условия 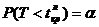 .
.
При α=0,05 и l=50-1=49 в таблице t-распределения, используя криволинейную интерполяцию, находим 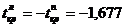 . Таким образом, критическая область
. Таким образом, критическая область 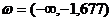 . Рассчитаем tr, полагая
. Рассчитаем tr, полагая 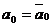 :
:
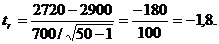
Значение -1,8 попадает в критическую область, поэтому нулевая гипотеза Н0 должна быть отвергнута. Следовательно, фирма в рекламе завышает срок безотказной работы изделия.
Сравнение двух дисперсий.
Пусть имеются две случайные величины 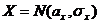 и
и 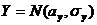 с неизвестными дисперсиями и две независисмые выборки х1, х2 ,..., хn и y1, y2 ,..., ym. Требуется по выборочным оценкам
с неизвестными дисперсиями и две независисмые выборки х1, х2 ,..., хn и y1, y2 ,..., ym. Требуется по выборочным оценкам
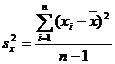 и
и 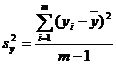 , где
, где 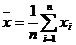 и
и 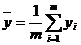 ,
,
проверить гипотезу 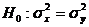 .
.
В качестве критерия при проверке гипотезы 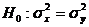 используют функцию
используют функцию
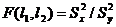 ,
,
которая имеет F-распределение (распределение Фишера-Снедекора) с l1=n-1 и l2=m-1 степенями свободы, если полученные по выборкам значения 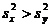 , и
, и
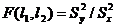
с l1=m-1, l2=n-1, если 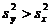 .
.
Если задаться уровнем значимости α, то можно построить критичские области для проверки гипотезы 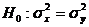 при двух альтернативных гипотезах:
при двух альтернативных гипотезах:
1) 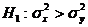 , если
, если 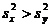 , или
, или 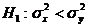 , если
, если 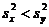 . В этом случае критическая область правосторонняя
. В этом случае критическая область правосторонняя 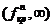 , где
, где 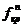 определяется из условия
определяется из условия 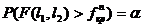 ;
;
2) 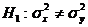 . В этом случае критическая область двусторонняя. Однако можно использовать только правостороннюю область
. В этом случае критическая область двусторонняя. Однако можно использовать только правостороннюю область 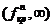 , где
, где 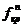 определяется из условия
определяется из условия 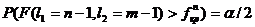 , если
, если 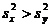 , и из условия
, и из условия 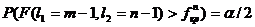 , если
, если 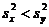 .
.
Если fr попадает в критическую область, то принимается альтернативная гипотеза Н1, в противном случае принимается гипотеза 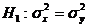 ; при этом оценкой генеральной дисперсии служит величина
; при этом оценкой генеральной дисперсии служит величина
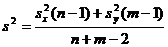 .
.
Задача 2. Срок хранения продукции, изготовленной по технологии А, составил:
| Срок хранения | xi | |||
| Число единиц продукции | ni |
а изготовленной по технологии В:
| Срок хранения | yi | ||||
| Число единиц продукции | mi |
Предположив, что случайные величины X и Y распределены по нормальному закону, проверить гипотезу 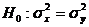 при уровне значимости 0,1 и альтернативной гипотезе
при уровне значимости 0,1 и альтернативной гипотезе 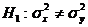 .
.
Решение. Вычислим «исправленные» выборочные дисперсии 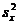 ,
, 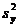 . Для этого вначале найдем
. Для этого вначале найдем 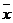 ,
, 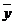 :
:
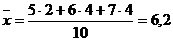 ;
; 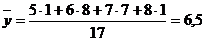 .
.
Тогда
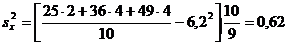 ;
;
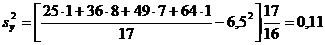 .
.
Учитывая, что 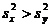 , определим fr:
, определим fr:
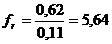 .
.
Критическое значение 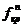 находим из условия
находим из условия
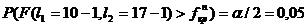 .
.
По таблице F-распределения определяем 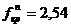 .
.
Так как число fr=5,64 попадает в критическую область 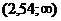 , то гипотезу о равенстве дисперсий среднего срока хранения продукции, изготовленной по технологиям А и В, отвергаем.
, то гипотезу о равенстве дисперсий среднего срока хранения продукции, изготовленной по технологиям А и В, отвергаем.
