Схема независимых испытаний. Простейший поток событий

Смоленск 2009

Если при проведении испытаний вероятность события А не зависит от исходов других испытаний, то такие события называются независимыми.

Формула Бернулли определяет вероятность появления ровно m раз события A в серии из n независимых испытаний, в каждом из которых вероятность появления события A равна p:

P_n(m)= 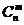p^mq^n-m,

где 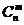= 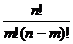, q=1-p.

При больших n ималеньких p вычисления по формуле Бернулли затруднены. В этих случаях используется формула Пуасона

P_n(m)≈ 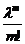e^{- λ}, λ=n∙p.

Цель занятия: 1. Научить студентов в конкретных ситуациях распознавать схему независимых испытаний и научить подбирать соответствующую формулу для вычисления вероятностей:

n-мало формула Бернулли

P_n(k) 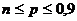формула Лапласа

n-велико

p<0,1 формула Пуассона,

хотя формула Лапласа на данном занятии и не используется.

2. Закрепить в сознании студента понятие простейшего потока событий. При решении задач обратить внимание студентов на то, что 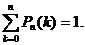Полезно обратить внимание студентов и на многообразное содержание, которое может быть вложено в схему независимых испытаний. При решении задач №5 и №6 подробно обсудить условия (отсутствие последствия, ординарность), определяющие простейший поток событий.

Задача 1.Каждый пятый клиент банка приходит брать проценты со вклада. Сейчас в банке ожидают своей очереди обслуживания шесть человек. Найти вероятность того, что из них будут брать проценты: а) только два человека; б) хотя бы один.

Решение.В задаче реализуется схема испытаний Бернулли. Здесь A – «человек в очереди будет брать проценты», тогда вероятность «успеха» p=1/5, а вероятность «неудачи» q=4/5.

а) P₆(2)= = ,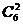

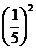
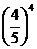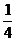б) P₆(m≥1)=1-P₆(0)=1- ≈ .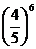

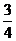Задача 2. На каждый вопрос предлагается три ответа, среди которых следует выбрать правильный. Задано пять вопросов. Какова вероятность того, что путем простого угадывания удастся правильно ответить на четыре вопроса? Какова вероятность правильно ответить хотя бы на один вопрос?

Решение. Выбор ответа на каждый вопрос можно рассматривать как независимое испытание, вероятность «успеха» в котором p = 1/3. Тогда вероятность правильно ответа на четыре вопроса равна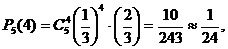

вероятность угадать ответ хотя бы на один вопрос равна

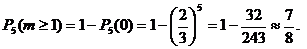
Задача 3.В среднем 20% пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций в результате торгов по первоначально заявленной цене: 1) не будут проданы 5 пакетов; 2) будет продано а) не менее 2 пакетов; б) не более 2; в) хотя бы 2 пакета.

Решение. 1) Вероятность того, что пакет акций не будет продан по первоначально заявленной цене, p=1-0,2=0,8.

По формуле Бернулли

P_5,9= 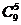∙0,8⁵∙0,2⁴=0,066.

2.а) По условию p=0,2.

P₉(m<2)=P_0,9+P_1,9= 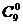∙0,2⁰∙0,8⁹+ 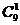∙0,2∙0,8⁸=0,436.

2.б) P₉(m≤2)=P_0,9+P_1,9+P_2,9= 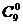∙0,2⁰∙0,8⁹+ 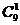∙0,2∙0,8⁸+ 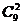∙0,2²∙0,8⁷==0,738.

2.в) P₉(m≥2)=P_2,9+P_3,9+...+P_9,9.

Указанную вероятность можно найти проще, если перейти к противоположному событию, т.е.

P₉(m≥2)=1-P₉(m<2)=1-(P_0,9+P_1,9)=1-0,436=0,564.

Задача 4. Вероятность попадания торпеды в корабль равна 0,3. Сколько можно выпустить торпед, чтобы вероятность поражения цели была больше 0,9.

Решение. На языке схемы испытаний Бернулли за «успех» считаем попадание торпеды в корабль, за «неудачу» — промах, тогда вероятность «успеха» p = 0,3, а «неудачи» — q = 0,7. Цель будет поражена, если в n выстрелах будет хотя бы одно попадание, т. е.

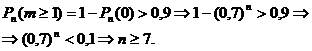
Задача 5. Вероятность того, что изделие при транспортировке повредится равна 0,0005. С завода отправлено четыре тысячи изделий. Найти вероятность того, что в пути повредится больше двух изделий.

Решение.Так как n велико, а p мало, то удобно пользоваться формулой Пуассона, p = 0,0005,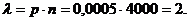

Нас интересует вероятность

Р₄₀₀₀(m > 2) = P₄₀₀₀ (3) +…+P₄₀₀₀(4000).

Проще вычислить эту вероятность, если рассмотреть противоположное событие:

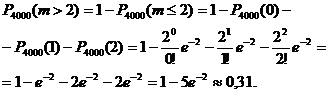
Задача 6. В течение часа на коммутатор поступает в среднем 120 телефонных вызовов. Какова вероятность того, что в течение заданной минуты поступит четыре вызова?

Решение. Телефонные вызовы поступают независимо друг от друга и по одному, т.е. выполняется условия простейшего потока событий. Значит, все вероятности определяются средним числом событий 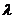.В нашем случае на интервал времени t=Iмин. приходится в среднем 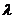= =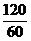2 вызова. Поэтому по формуле Пуассона: Р(4)= 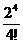е .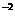

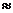
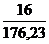
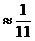Задача 7.Известно, что наборщик в среднем допускает одну ошибку на две страницы текста. В набранной книге взяли наугад страницу. Какова вероятность того, что на ней нет опечаток? Какова вероятность того, что на ней больше одной опечатки?

Решение.Опечатки появляются независимо друг от друга и по одной. Условия простейшего потока приблизительно выполняются и формула Пуассона приблизительно верна. На одну страницу приходится в среднем 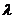= 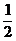опечатки. Поэтому

Р(0)= 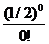е 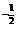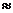0,6. Р(m>1)=1–Р(0)–Р(1)=1–0,6–0,3=0,1.

Задача 8. На факультете насчитывается 500 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно для m студентов данного факультета? Вычислить указанную вероятность для значений m = 0, 1, 2, 3.

Решение.Так как n = 500 >1 и р = Р {родится 1 сентября любому из студентов факультета} = 1/365 < 1, то можно использовать формулу Пуассона с параметром l = 1,36986. Находим

P₅₀₀(0)= e^{- λ} ≈ 0,2541,

P₅₀₀(1)= 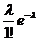≈ 0,3481,

P₅₀₀(2)= 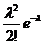≈ 0,2385,

P₅₀₀(3)= 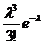≈ 0,1089.

Значения искомых вероятностей, соответствующих биноминальному распределению В(500, 1/365) и вычисленных с 4 верными знаками после запятой, таковы:

P₅₀₀(0) = 0,2537, P₅₀₀ (1) = 0,3485, P₅₀₀(2) = 0,2389, P₅₀₀(3)= =0,1089.

Дополнительные задачи.

Задача 1.Вероятность малому предприятию быть банкротом за время t равна 0,2. Найти вероятность того, что из восьми малых предприятий за время t сохранятся: а) два; б) не более двух.

Ответ: а) P_2,6= 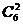p²q⁴=0,717; б) P₆(m>2)=1-P₆(m<2)=

=1-(P_0,6+P_1,6)=0,999.

Задача 2. Предполагается, что 10% открывающихся вновь малых предприятий прекращает свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность?

Ответ: P₆(m≤2)=P_0,6+P_1,6+P_2,6=0,984.

Задача 3. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье: а) не менее трех мальчиков; б) не более трех мальчиков.

Ответ: а) P₁₀(m≥3)=1-P₁₀(m<3)=1-(P_0,10+P_1,10+P_2,10)=0,945; б) P₁₀(m≤3)=P_0,10+P_1,10+P_2,10+P_3,10=0,172.

Задача 4. Два равносильных противника играют в шахматы. Что более вероятно: а) выиграть 2 партии из 4 или 3 партии из 6?; б) не менее 2 партий из 4 или не менее 3 партий из 6? (Ничьи в расчет не принимаются).

Ответ: а) 2 партии из 4, ибо P_2,4= 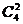p²q²=0,375, а P_3,6= 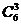p³q³=0,312; б) не менее 2 партий из 4, ибо P₄(m≥2)=P_2,4+P_3,4+P_4,4=0,688, а P₆(m≥3)=1-P₆(m<3)=1-(P_0,6 + +P_1,6+P_2,6)=0,656.

Задача 5. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено: а) три ошибочно укомплектованных пакета; б) не более трех пакетов.

Ответ: а) P_3,4000=P₃(0,4)=0,00715; б) P₄₀₀₀(m≤3)=P_0,4000+ +P_1,4000+P_2,4000+P_3,4000=0,9992.

Домашнее задание.

Задача 1. Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из этих покупателей потребуется холодильник марки «А», равна 0,4. Найти вероятность того, что холодильник потребуется:

а) не менее, чем двум покупателям;

б) не более, чем трем покупателям;

в) всем четырем покупателям.

Задача 2. Работают четыре магазина по продаже стиральных машин. Вероятность отказа покупателю в магазинах равна 0,1. Считая, что ассортимент товара в каждом магазине формируется независимо от других, определить вероятность того, что покупатель получит отказ в двух, в трех и в четырех магазинах.

Задача 3. Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара равна 0,01. Найти вероятность того, что из проданных пар обуви будет возвращено а) ровно 4 пары, б) ровно 5 пар.

Задача 4. В новом микрорайоне поставлено 10 000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна а) 0,0002; б) 0,001. Найти вероятность того, что за месяц откажут два, три и пять замков.

Задача 5. На станциях отправления поездов находится 1000 автоматов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,004. Какова вероятность того, что в течение часа из строя выйдут два, три и пять автоматов?

Ответы: 1) а) P(X≥2)=0,5248; б) P(X≤3)=0,9744; в) P(X=4)=0,0256. 2) P₄(2)=0,0486; P₄(3)=0,0036;P₄(4)=0,0001. 3) а) P₂₀₀(4)=0,09; б) P₂₀₀(5)=0,036. 4) б) P₁₀₀₀₀(2)=0,00225; P₁₀₀₀₀(3)=0,0075; P₁₀₀₀₀(5)=0,0375; 5) P₁₀₀₀(2)=0,1464; P₁₀₀₀(3)=0,1952; P₁₀₀₀(5)=0,1562.

СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Г. С. ЕВДОКИМОВА

ПРАКТИКУМ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

МОДУЛЬ 5

Случайные величины.

Законы распределения