Тема 4: условная вероятность, зависимость и независимость событий. формула байеса

При совместном рассмотрении двух случайных событий AиBчасто возникает вопрос: насколько связаны эти события друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого?

Для характеристики зависимости одних событий от других вводится понятие условной вероятности. Пусть 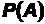≠0, тогда отношение 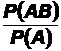называется условной вероятностью события В при условии наступления события А. Такая вероятность обозначается P(B/A). По определению имеем следующее равенство:

P(B/A)= .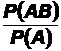

Теорема 1 (умножения вероятностей). Вероятность совместного наступления двух событий равна вероятности одного из этих событий при условии другого, умноженной на вероятность самого условия:

.

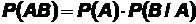Утверждение теоремы непосредственно следует из определения условной вероятности и допускает распространение на случай большего числа сомножителей:

P( )= .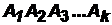

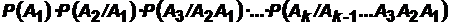Если появление событияАне зависит от того, произошло или нет событиеВ, то условная вероятностьА в предположении, что событие Внаступило, будет равна вероятности А, т.е. P(A/B)=P(A). Подставляя в формулу умножения вероятностей вместо P(A/B) вероятностьP(A), получим: P(AB)=P(A)·P(B).

Если это соотношение выполняется, то событияАиВназываются независимыми.

Утверждение 1. Пусть событияАиВ– независимы. Тогда независимы также события 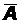иВ, Аи 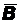, 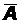и .

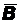Несколько событий называют попарно независимыми, если каждые два из них независимы.

Несколько событийназывают независимыми в совокупности, если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Отметим, что требование независимости событий в совокупности сильнее требования их попарной независимости.

Утверждение 2. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

.

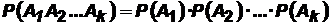Если события 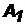, ,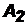…, 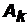- независимы в совокупности, то и противоположные им события 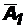, ,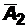…, 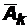также независимы в совокупности.

Теорема 2. Вероятность появления хотя бы одного из событий 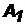, ,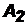…, , 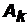независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:

.

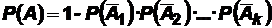Следствие. Если события 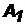, ,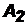…, 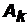имеют одинаковую вероятность, равную p, то вероятность появления хотя бы одного из этих событий 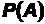=1- 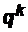, где q=1-p.

Теорема 3. Если событие Aможет произойти только при условии появления одного из событий (гипотез) 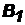, , 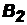…, , 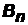образующих полную группу, то вероятность события A равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события A:

.

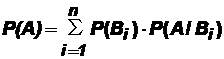Указанная формула называется формулой полной вероятности.

В тесной связи с формулой полной вероятности находится так называемая формула Байеса. Она относится к той же ситуации, что и формула полной вероятности (событие Aможет наступить только вместе с одним из n попарно несовместных событий 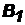, , 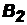…, 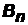). Допустим, что опыт уже произведен, и нам известно, что событие A наступило. Сам по себе этот факт еще не позволяет сказать, какое из событий 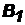, , 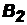…, 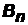имело место в проделанном опыте. Можно, однако, поставить такую задачу: найти вероятности 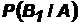, …, 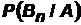каждой из гипотез в предположении, что наступило событие A (такие вероятности называются апостериорными в отличие от вероятностей 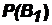, …, , 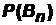вычисляемых до опыта и называемых априорными).

С одной стороны, вероятность совмещения двух зависимых событий определяется по формуле: ,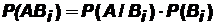

а с другой стороны, имеем: 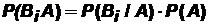. Приравнивая правые части, получим: 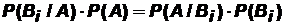, откуда следует: 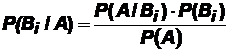, где знаменатель рассчитывается по формуле полной вероятности. Таким образом, апостериорная вероятность определяется по формуле:

,

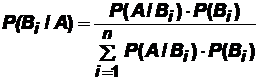которая называется формулой Байеса. Запомнить ее нетрудно: в знаменателе стоит выражение для полной вероятности события A, а в числителе – одно из слагаемых этого выражения. Формула Байеса дает возможность «пересмотреть» вероятности гипотез с учетом наблюдавшегося результата опыта.

Задачи для самостоятельного решения:

4.1Известно, что P(A)>0,5;P(B)>0,8.Могут ли такие события AиB:

а) быть несовместными;

б) быть противоположными;

в) верно ли неравенство P( 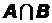)>0,2?

4.2Вероятность для человека, поступившего в университет, закончить первый курс равна P; вероятность проучиться успешно до пятого курса и закончить его равнаQ. Какова вероятность для второкурсника успешно закончить пятый курс?

4.3При включении зажигания двигатель начинает работать с вероятностью 0,6. Найти вероятность того, что:

а) двигатель начнет работать при третьем включении зажигания;

б) для запуска двигателя придется включать зажигание не более трёх раз.

4.4Два охотника стреляют по летящей утке. Шансы попадания оцениваются для первого охотника как 90%, а для второго – 80%. Найти вероятность того, что птичке не спастись.

4.5 6шаров (4белых и 2чёрных) случайным образом раскидали в два ящика по три шара в каждый.

а) Какова вероятность того, что ровно один чёрный шар попал в первый ящик?

б) Из первого ящика достали шар, он оказался белым. Какова вероятность того, что ровно один чёрный шар попал в первый ящик?

4.6Из ящика, содержащего чёрные и белые шары, 100раз подряд извлекли чёрный шар. Какова вероятность того, что и в 101-й раз будет извлечен чёрный шар? Рассмотреть два случая: выбор шаров производился без возвращения; выборка была с возвращением.

4.7При обследовании на СПИД вероятность обнаружить ВИЧ у инфицированного человека равна 0,9. Вероятность принять здорового человека за больного равна 0,01. Пусть доля инфицированных по отношению ко всему населению равна 0,0001. Найдите условную вероятность того, что человек не инфицирован, если при обследовании у него обнаружен ВИЧ.

4.8Страховая компания разделяет застрахованных водителей на три группы по вероятности попадания в дорожную аварию. Среди застрахованных водители группы с низкой вероятностью составили 25%, со средней – 60% и с высокой – 15%. Ниже приведена таблица вероятностей попадания водителей каждой группы в аварию:

Риск водителя	Вероятность попадания в аварию
низкая	средняя	высокая
1 авария в год	0,01	0,03	0,10
2 аварии в год		0,01	0,05
3 аварии в год			0,01
4 аварии в год

Требуется найти:

а) если случайно выбранный водитель не попадал в аварию в течение года, какова вероятность того, что он принадлежит к группе водителей с высокой вероятностью попадания в дорожную аварию?

б) если случайно выбранный водитель не попадал в аварию в течение четырех лет, какова вероятность того, что он принадлежит к группе водителей с низкой вероятностью попадания в дорожную аварию?

4.9Институт дистанционного обучения отправил учебники в три своих филиала. Вероятность своевременной доставки в первый филиал равна 0,9; во второй – 0,95; в третий – 0,8. Найти вероятности следующих событий:

а) только один филиал получит учебники вовремя;

б) хотя бы один филиал получит учебники с опозданием.

4.10Фирма имеет три источника поставки комплектующих – заводыА, В и С. На долю завода А приходится 50% общего объема поставок; В – 30% и С– 20%. Из практики известно, что 10% поставляемых заводом А деталей бракованных, заводом В – 5% и заводом С – 6%. Определите вероятности следующих событий:

а) взятая наугад деталь была получена от заводаА;

б) взятая наугад и оказавшаяся бракованной деталь, была получена от завода А.

4.11Каждое изделие с вероятностью 0,01 дефектно. Контроль может пропустить дефектное изделие с вероятностью 0,10, и забраковать годное с вероятностью 0,05. Определить:

а) вероятность приемки наудачу взятого изделия;

б) процент годных изделий среди принятых.

4.12В начале года капитал фирмы составлял1млн.руб. Каждый месяц капитал равновероятно увеличивается или уменьшается на 200 тыс. руб. Найти риск разорения фирмы за полгода.

4.13Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в 1, 2 и 3 справочнике соответственно равна 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится:

а) только в одном справочнике;

б) только в двух справочниках;

в) во всех трех справочниках;

г) хотя бы в одном справочнике;

д) ни в одном справочнике.

4.14В районе 24 человека обучаются на заочном отделении университета, из них 6 – на юридическом факультете, 12 – на географическом и 6 – на экономическом.Вероятность успешно сдать все экзамены на предстоящей сессии для студентов юридического факультета равна 0,6, географического – 0,76 и экономического – 0,8. Найти вероятность того, что наудачу взятый студент, сдавший успешно все экзамены, окажется студентом экономического факуль-

тета.

4.15В трех параллельных группах была проведена одна и та же контрольная работа. В первой группе обучаются 30 студентов, во второй – 28, в третьей – 27. Выполненных на «отлично» в первой группе оказалось 8 работ, во второй – 6, в третьей – 9. Найти вероятность того, что первая взятая наудачу при повторной проверке работа, из работ, принадлежащих группе, которая также выбрана наудачу, окажется выполненной на «отлично».

4.16ДаноP(A)=0,8; P(A∩B)=0,5; P(A/B)=0,9. Найти P(B), P(B/A), P(AUB) и выяснить, зависимы ли события 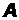и .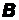

4.17Вероятность попадания в цель равна 0,3, а вероятность ее уничтожения равна 0,05. Найти вероятность того, что при попадании в цель она будет уничтожена.

4.18В произвольном порядке выписываются две буквыИи две буквы С. Найти вероятность того, что обе буквы С стоят рядом, при условии, что последняя по порядку буква есть буква И.

4.19Из колоды в 36 карт берется наудачу одна карта. Зависимы ли событияА – «выбран валет» и В – «выбрана карта черной масти»?

4.20Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,3, второй – 0,4, третий – 0,5. По условиям приема события, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.

4.21Монета бросается до первого появления герба. Какова вероятность того, что понадобится четное число бросков?

4.22Из буквА, А, И, Л, М, Н разрезной азбуки выбирают наудачу по одной и ставят в ряд. Найти вероятность того, что получится слово:

а)МИНА; б)НАЛИМ; в)МАЛИНА?

ТЕМА 6: МОДЕЛЬ ПОВТОРНЫХ НЕЗАВИСИМЫХ ИСПЫТАНИЙ: