Тема 5. Расположение корней квадратного трехчлена в зависимости от значений параметра

Пусть дано уравнение 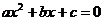. Рассмотрим функцию 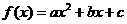и М – точка на оси Ох.

1) Найти набор условий, при котором все корни уравнения меньше М

Ход решения:

Данная функция в зависимости от значения параметра перед старшим членом может оказаться параболой или линейной функцией. Рассмотрим оба этих случая:

• Пусть а=0, и дана линейная функция.

Тогда 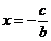и нужно поставить условие .

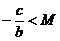• Пусть 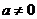, и дана квадратичная функция.

Тогда мы можем найти корни уравнения 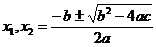и проверить условие, что оба корня меньше М. Однако в некоторых случаях (например, когда дискриминант не является полным квадратом) такая проверка достаточно трудозатратна и сложна чисто арифметически. В этом случае можно не находить корни, а поставить ряд условий, которые позволят совершенно точно задать нужное нам расположение параболы.

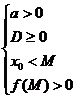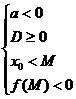или , где х₀ – координата х вершины параболы.

Можно проверить эти два случая (ветви параболы направлены вверх или вниз) в одной системе:

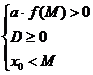
2) Найти набор условий, при котором все корни уравнения больше М

Здесь и далее общий ход решения такой же, как в первом примере, поэтому далее будут указываться только система условий для случая, когда дана квадратичная функция, а корни находить неудобно и долго.

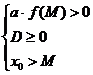
3) Найти набор условий, при котором один из корней уравнения меньше, а другой - больше М

Здесь уже очевидно, что речь идет о квадратичной функции, так как корней два, поэтому случай с линейной функцией можно не проверять.

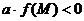
Пусть дано уравнение 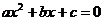. Рассмотрим функцию 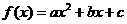и М, N – точки на оси Ох.

4) Найти набор условий, при котором все корни уравнения лежат в интервале от М до N

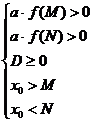
5) Найти набор условий, при котором один корень уравнения меньше М, а второй – больше N

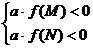
Задания, связанные с условиями на импликацию

Импликация – логическая связка, по смыслу схожая с союзами «если… то».

Импликация записывается как посылка => следствие.

Пример:

Пусть существуют множества А и В, при этом А входит в В, т.е. является его подмножеством. Тогда верна следующая логическая связка: если число 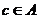, следовательно, .

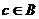Лекция 6. Обратная функция. Иррациональные. Дробные степени

Понятие обратной функции

Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.

Обратная функция функции 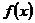{\displaystylef} обычно обозначается .

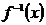Чтобы для функции 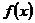найти обратную функцию 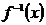, нужно в уравнении 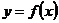вместо 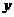подставить 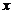, а вместо 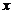— 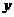и решить его относительно 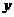(выразить 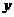через 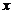). Если оно имеет более чем один корень, то функции, обратной к {\displaystylef} 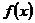, не существует.

Функция {\displaystylef(x)} 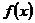обратима на некотором интервале {\displaystyle (a;b)}тогда и только тогда, когда на этом интервале она взаимно-однозначна, т.е. каждому значению аргумента соответствует ровно однозначение функции, и наоборот, каждое значение функции достигается только при одном значении аргумента.

Пример. ,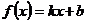

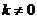
Ищем обратную: 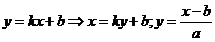. Обратная функция: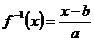

Пример.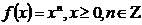

Обратная: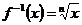

Теорема. Так как переход к обратной функции происходит с помощью замены 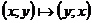, графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

Функция 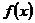{\displaystylef} является обратной к 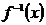. Функции 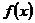{\displaystylef} и 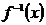называются взаимно обратными.

2. Свойства взаимно обратных функц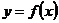ий 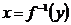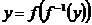и .

· и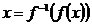

· Область определения функции 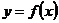совпадает с областью значений функции 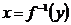и наоборот. ,

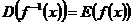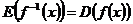
· Графики взаимно обратных функций симметричны относительно прямой .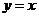

· Если 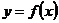возрастает, то и 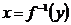возрастает, если 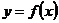убывает, то и 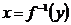убывает.

{\displaystylef^{-1}}3. Основные свойства степеней:

1) Если m и n – натуральные числа, то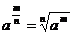

2)

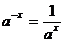
3)

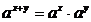
4)

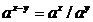
5)

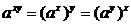
6)

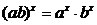
7)

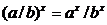
8)

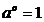
9)