Деление отрезка в заданном соотношении
Пусть даны две точки 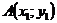 и
и 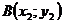 . Нужно найти координаты точки
. Нужно найти координаты точки 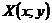 , которая делит этот отрезок в соотношении c:d.
, которая делит этот отрезок в соотношении c:d.
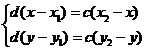 ,
,
Уравнениепрямой
· уравнениепрямой с угловым коэффициентом
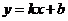
· каноническая форма уравнения прямой
Пусть нужно найти уравнение прямой по точке 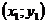 и направляющему вектору
и направляющему вектору 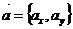 , т.е. ненулевому вектору, лежащему на искомой прямой или параллельному ей.
, т.е. ненулевому вектору, лежащему на искомой прямой или параллельному ей.
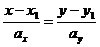
Частный случай: уравнение прямой по двум точкам
Пусть даны две точки 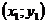 и
и 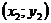 . Уравнение прямой, проходящей через эти две точки:
. Уравнение прямой, проходящей через эти две точки:
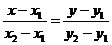
- параметрическая форма уравнения прямой
Пусть нужно задать прямую в параметрической форме по точке 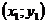 и направляющему вектору
и направляющему вектору 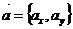 .
.
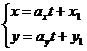
· общее уравнениепрямой
Пусть нужно найти уравнение прямой по точке 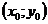 и нормальному вектору прямой
и нормальному вектору прямой 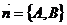 , т.е. ненулевому вектору, перпендикулярному искомой прямой.
, т.е. ненулевому вектору, перпендикулярному искомой прямой.
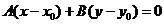
Обычно общее уравнение прямой записывают в виде
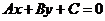
Число решений системы линейных неравенств
| Форма задания прямой | Прямые параллельны, нет решений | Прямые совпадают, бесконечно много решений | Прямые пересекаются, одно решение | Частный случай: прямые перпендикулярны |
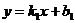 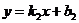 | 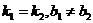 | k1=k2, b1=b2 | 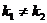 | k1*k2=-1 |
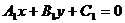 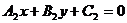 | 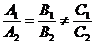 | 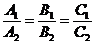 | 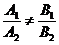 | 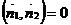 , то есть A1*A2 + B1*B2=0 , то есть A1*A2 + B1*B2=0 |
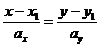 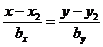 | 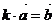 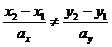 или или 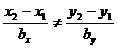 | 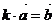 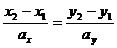 или или 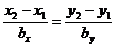 | 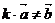 | 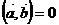 |
Лекция 3. Модули
Напомнимопределениемодуляиегоосновныесвойства.
Определение. Абсолютнойвеличиной (илимодулем) |х| называетсясамоэточисло, еслих‑положительноечисло; нуль, есличислох‑нуль; число, противоположноечислух, еслих‑отрицательноечисло.
Этоопределениеможнозаписатьвдругойформе:
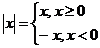
Теорема.Свойствамодулядействительногочисла:
1.│а+в│≤│а│+│в│;
2.│ав│=│а│*│в│;
3.│1/а│=1/│а│приа≠0;
4.│а-в│≥││а│-│в││.
Схемырешениярациональныхуравнений/неравенствсмодулями
1. Схема |f(x)| = c.
Прис< 0 –нетрешений.
Прис = 0 f(x) = 0.
Прис> 0 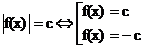 .
.
Пример 2. 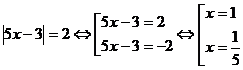 . Ответ:
. Ответ: 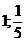 .
.
2. Схема |f(x)| ≥c.
Прис≤ 0–D(f), тоестьвсечисла, прикоторыхопределенафункцияf(x).
Прис> 0 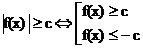 .
.
Пример 3. 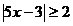 . Ответ:
. Ответ: 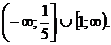
3. Схема |f(x)| ≤c.
Прис< 0–нетрешений.
Прис = 0f(x) = 0.
Прис>0 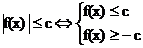 .
.
Пример 4. 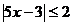 . Ответ:
. Ответ: 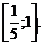
4. Схема |f(x)| = g(x).
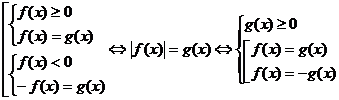 .
.
Выбор схемы зависит от того, какое неравенство легче решать – на f(x) или на g(x).
5. Схема |f(x)| ≥ g(x).
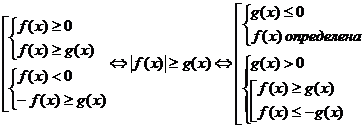
Выбор схемы зависит от того, какое неравенство легче решать – на f(x) или на g(x).
6. Схема |f(x)| ≤ g(x).
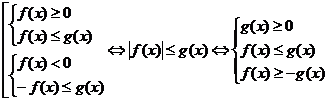
Выбор схемы зависит от того, какое неравенство легче решать – на f(x) или на g(x).
Методинтерваловдлямодулей
Применяетсявуравненияхинеравенствахтипа |f(x)| + |g(x)| = h(x) иимподобных, тоестьтам, гдеестьнесколькомодулейионинезависятдруготдруга (втомсмысле, чтонеявляютсявложенными). Вслучаевложенныхмодулейнадораскрыватьотвнешнегоквнутреннемуилинаоборот–взависимостиотвозможныхупрощений, новодномпорядке.
Схема метода интервалов для модулей. Разбиваем числовую ось точками, в которых подмодульные выражения равны нулю, на промежутки знакопостоянстваподмодульных выражений. На каждом промежутке раскрываем модули (в зависимости от знака подмодульного выражения), решаем уравнение или неравенство, пересекаем получающийся ответ с промежутком. Затем объединяем полученные на всех промежутках ответы.
Напомним:
1.y=|f(x)| - часть графика, находившаяся выше оси Ох, остается неизменной, а часть графика, находившаяся ниже этой оси, симметрично отображается относительно Ох
2. y=f(|x|) – часть графика, находившаяся правее оси Оy, остается неизменной и симметрично отражается влево относительно оси Oy.
3. |y|=f(x) – часть графика, находившаяся выше Ох остается неизменной и симметрично отражается вниз относительно Ох, а часть графика, находившаяся ниже оси Ох стирается.

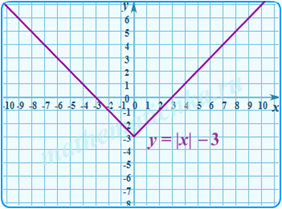
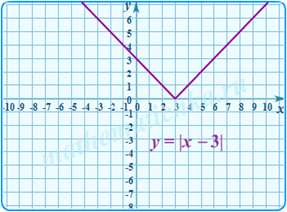
y=|x-a|
Сделаем математику красивее…
Построить множество точек, задающееся уравнением 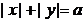
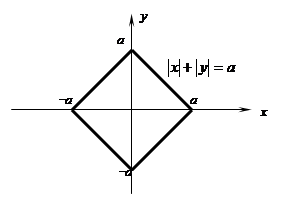
Комментарий: а–половинадиагоналиквадрата.
Геометрическийцентрквадрата– (0;0).
Чётнопохиу, тоесть, строимвпервойчетверти
иотражаемвовсечетыре.
Построить множество точек, задающеесяуравнением 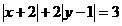


Сумма модулей
Если функция является суммой или разностью нескольких модулей, следует разбить координатную плос-кость на участки и построить часть графика на каждом из участков отдельно. Границы участков определяют-ся значениями переменных, при которых обнуляется один из модулей. Таким образом, эти границы можно найти с помощью приравнивания каждого модуля к нулю и решением соответствующего уравнения.
Пример 3.
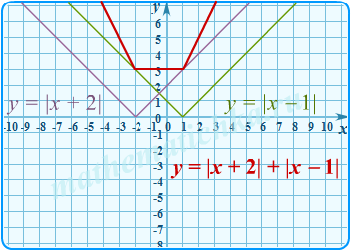
Построить график функции y = |x + 2| + |x − 1|.
Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, иследовательно, 2 уравнения, каждое из которых имеет одно решение, следовательно, 2 границы, которыми плоскость разби-та на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.
На одних осях независимо друг от друга строим графики функций y = |x + 2| и y = |x − 1|, используя сдвиг и отражение. Складываем ординаты в точках излома x = −2 и x = 1 и в двух удобных точках на крайних участ-ках, например, при x = −3 и x = 3. На приведенном рисунке красным цветом представлен результирующий график, полученный по этим 4-ём точкам: (−3;5 ), (−2;3 ), (1; 3), (3;7).
Запомните:Если y1 = k1x+b1и y2 = k2x+b2, то их сумма:!
Ysum = y1+y2 = (k1+k2)x + (b1+b2)