Определение параметров эмпирической зависимости

Часто из физических соображений следует, что зависимость между величинами хорошо описывается моделью вида , где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров 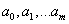из условия минимума функции: .

ПРИМЕР 3. Вывод нормальной системы уравнений для нахождения параметров эмпирической зависимости.

Выведем систему уравнений для определения коэффициентов и функции , осуществляющей среднеквадратичную аппроксимацию заданной функции по точкам. Составим функцию и запишем для нее необходимое условие экстремума:

Тогда нормальная система примет вид:

Получили линейную систему уравнений относительно неизвестных параметров, которая легко решается.

Если зависимость от параметров нелинейна, то экстремум функции ищут методами минимизации функций нескольких переменных.

Многочлены Бернштейна

Предположим, что функция 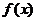задана в отрезке [0,1] в точках , при некотором фиксированном n. В этом случае можно построить многочлен Бернштейна:

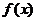Можно доказать, что при многочлены стремятся к функции равномерно по x; кроме того, для любого конкретного целого имеет место предельное соотношение для производных:

Наконец, известно, что если число удовлетворяет неравенству на всем отрезке [0,1], то для любого 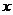из этого отрезка выполняется неравенство: .

Это, конечно, позволяет оценивать ошибку, которая возникает при соответствующей интерполяционной замене.

Сказанное выше для случая функции 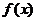одной переменной можно обобщить на случай двух и более переменных. Мы ограничимся обобщением только на случай двух переменных.

Итак, пусть имеется функция на квадрате

,

причем реально она задана в узлах решетки

,

при заранее фиксированных натуральных числах 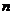и . Построим по этой информации следующий многочлен от двух переменных:

,

где - биномиальные коэффициенты. Это - многочлен Бернштейна для заданной функции на заданной решетке. С его помощью так же можно осуществлять интерполяцию, принимая его значение в той или иной точке квадрата за значение самой функции. Можно доказать, что для любой точки квадрата имеет место неравенство:

,

которое позволяет оценить погрешность интерполяции. (Здесь константы и удовлетворяют в рассматриваемом квадрате неравенствам).

.

Замечание.Случай одной переменной рассматривался выше на отрезке [0, 1], а случай двух переменных - в единичном квадрате. В действительности, рассмотрения возможны на любом отрезке [a,b] и на любом прямоугольнике [a,b;c,d]. Для этого в исходной ситуации (т.е. на произвольном отрезке или на произвольном прямоугольнике нужно сделать линейную замену переменных).

Подробнее: пусть функция 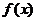задана в точках отрезка , где при некотором фиксированном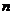

Положим

тогда

если теперь в 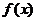положить , то возникнет ситуация функции , заданной уже на отрезке [0, 1]. Аналогично, в случае двух переменных надо сделать замену:

,

после чего возникнет ситуация единичного квадрата.

Задание для самостоятельной работы

1. Построить приближение таблично заданной функции по методу наименьших квадратов многочленами 0-ой, 1-ой и 2-ой степеней.

X	-2	-1
Y	9.9	5.1	1.9	1.1	1.9

Построить графики функции и найденных многочленов.

2. Функция y=a/x+b задана таблицей своих значений.

x	0.1	0.2	0.5
y	10.22	5.14	2.76

Найти параметры a и b по методу наименьших квадратов.

Указание. Предварительно свести задачу к линейной, сделав замену: t=1/x. Тогда функция y приближается многочленом 1-ой степени a t+b.

3. Вывести нормальную систему уравнений для определения параметров a, b, c функции g(x)=a sin(x)+b cos(x)+c, осуществляющей среднеквадратичную аппроксимацию таблично заданной функции y(x).

Вопросы

1. Сформулируйте постановку задачи приближения функции по методу наименьших квадратов.

2. Что такое среднеквадратичное отклонение.

3. Как определить степень приближающего многочлена.

4. Из какого условия выводится нормальная система наименьших квадратов.

Интерполяция функций