Одинаково распределенные независимые случайные величины

Рассмотрим n взаимно независимых случайных величин 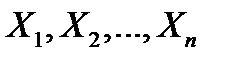, которые имеют одинаковые распределения, а следовательно и одинаковые характеристики.

Обозначим среднее арифметическое рассматриваемых случайных величин через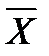

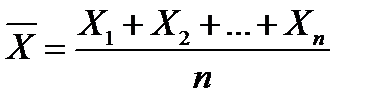
Математическое ожидание среднего арифметического n одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию a каждой из величин: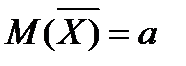

Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии каждой из величин: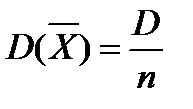

Среднее квадратическое среднего арифметического n одинаково распределенных взаимно независимых случайных величин в 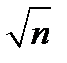раз меньше среднего квадратического каждой из величин:

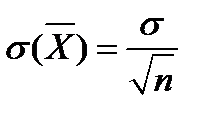
Непрерывные случайные величины (НСВ), их числовые характеристики

Случайную величину назовем непрерывной, если ее функция распределения непрерывна.

Легко видеть, что случайная величина непрерывна тогда и только тогда, когда 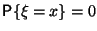при всех 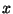. Важный класс непрерывных случайных величин - абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.

Числовые характеристики непрерывных случайных величин

Пусть непрерывная случайная величина Х задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [a,b].

Определение. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

Определение. Средним квадратичным отклонениемназывается квадратный корень из дисперсии

Вероятность попадания НСВ в заданный интервал

Вероятность попадания случайной величины Х в интервал ( 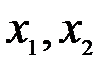) равна

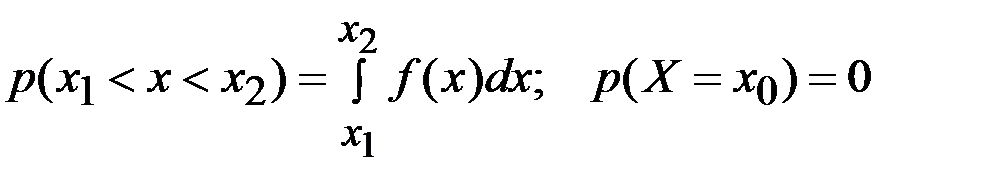
Примеры распределения НСВ

Равномерное распределение

Непрерывная случайная величина x , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения p_x (x) и функция распределения F_x (x ) имеют соответственно вид:

, .

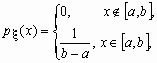
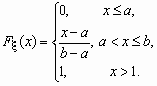
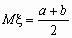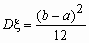Экспоненциальное (показательное) распределение

Непрерывная случайная величина x имеет показательное распределение с параметром l > 0, если она принимает только неотрицательные значения, а ее плотность распределения p_x (x )и функция распределения F_x (x) имеют соответственно вид:

, .

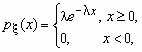
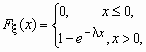
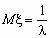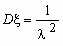Нормальное распределение

Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.

Случайная величина x нормально распределена с параметрами a и s , s >0, если ее плотность распределения p_x (x ) и функция распределения F_x (x) имеют соответственно вид:

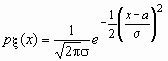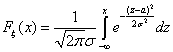, , Mx = a, Dx = s ²_.

Закон больших чисел

Закон больших чиселв теории вероятностейутверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Неравенство Чебышёва

Неравенство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего.