Локальная и интегральная теоремы Лапласса

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

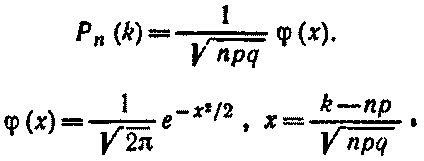
Для определения значений φ(x) можно воспользоваться специальной таблицей.

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

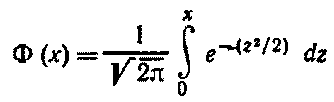-функция Лапласа

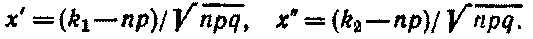
Значения функции Лапласа находят по специальной таблице.

Теорема Пуассона

При большом количестве испытаний вычисления по формуле Бернулли становятся затруднительными. Однако в ряде случаев их можно заменить более простыми асимптотическими формулами. Одна из них основана на теореме Пуассона.

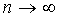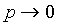Если число испытаний и так, ч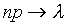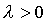то , , то 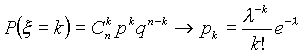при любых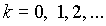

Это означает, что при больших nи малых p вместо вычислений по точной формуле

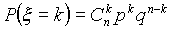
можно воспользоваться приближенной формулой ,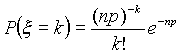

т.е. использовать формулу Пуассона для  =np.

Тема 2. Случайные величины и законы их распределения

Понятие случайной величины

Примеры дискретных случайных величин

Распределение Бернулли (или биномиальное распределение) определяется как закон распределения случайной величины, равной числу успехов в n испытаниях Бернулли. Эта случайная величина x может принять любое из значений 0, 1, 2, …, n, а их вероятности определяются формулой Бернулли: если p – вероятность успеха, q – вероятность неудачи, то

,

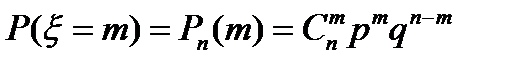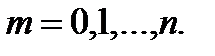
Распределение Пуассона. Случайная величина, распределенная по закону Пуассона, может принять любое из значений 0, 1, 2, … (счетное множество значений), а их вероятности задаются формулой

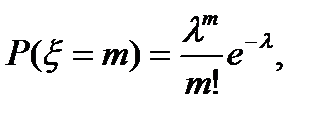
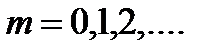, l>0.

Геометрическое распределение имеет случайная величина x, равная числу испытаний Бернулли до первого «успеха» (включительно) с вероятностью «успеха» в одном испытании равном р. Такая случайная величина принимает значения x=1, 2, 3,…, а их вероятности задаются формулой:

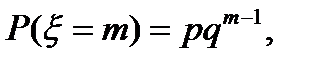
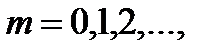
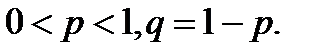
Гипергеометрическое распределение определяется, например, в задаче о выборке деталей. Пусть имеется N деталей, из которых M – стандартные. Делается выборка из n деталей. Случайная величина x определяется как число стандартных деталей в такой выборке. Оно может равняться любому числу от 0 до n, но, конечно, не больше, чем М, т.е. m=0,1,2,…,min(n,M). Вероятности этих значений определяются гипергеометрической формулой

,

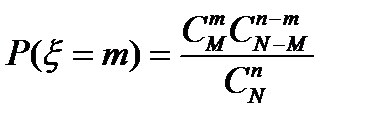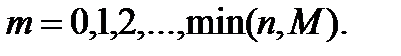
Функция распределения и плотность распределения

Функция распределения

Каждая случайная величина полностью определяется своей функцией распределения.

Если x .- случайная величина, то функция F(x) = Fx (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.

Функция распределения любой случайной величины обладает следующими свойствами:

1) F(x) определена на всей числовой прямой R;

2) F(x) не убывает, т.е. если x1 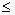x2, то F(x1) 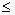F(x2);

3) F(- 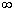)=0, F(+ 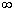)=1, т.е. 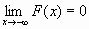и ;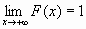

4) F(x) непрерывна справа, т.е.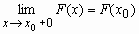

Плотность распределения

Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f (x) = F′(x).

Вероятность того,что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а,b), определяется равенством: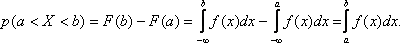

Зная плотность распределения, можно найти функцию распределения F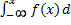(x)= x

Плотность распределения обладает следующими свойствами:

Свойство 1. Плотность распределения неотрицательна, т.е. f(x) ≥0

Свойство 2. Несобственный интеграл от плотности распределения в пределах от - 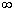до + 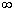равен единице: .

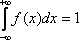В частности, если все возможные значения случайной величины принадлежат интервалу (a,b), то 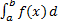x=1