Раздел 1. Теория вероятностей

Раздел 1. Теория вероятностей

Тема 1. Случайные события

Предмет теории вероятностей

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Опыт-это явление, происходящее при условиях, созданных человеком и которое может повторяться большое кол. раз. Результатом опыта наз. случайным событием.

Виды случайных событий:

1.достоверные Е(событие, кот. в усл. данного опыта обязательно происходит)

2.невозможное U(никогда не происходят в усл. данного опыта)

3.несовместные(если в усл данного опыта не происх. одновременно)

4.совместные(в условиях данного опыта м. появиться одновременно)

5.В благопрепятствует А,если из факта появленияВ вытекает факт появления А.

6.А и Ас чертой,к каждому событию А мож. сопоставить противопол. события, т.е такое событие, кот дополн А)

1.1.2.Вероятность события.

Вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений.

n-опыт

m,a-число опытов,при кот.события происх.

M(A)/n=ω(A)-частота проведения опытов

Классическое и статистическое определение вероятности

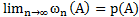–теорема Бернулли или статистическая вероятность события А

Классическая формула вероятности.

Обознач набором элементов исх.опыта.-наз. Множество событий{ 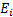}i=1

1.в результате опыта обязат. Происх одно из данных событий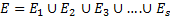

2.события 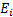попарно несовместны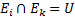

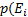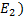3.статистич вероятность всех событий равны. )=p( =…=p( )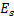

Геометрическая вероятность

Если пространство элементарных событий содержит бесконечное множество элементов и ему можно поставить в соответствие некоторое геометрическое пространство, а вероятность каждого события зависит только от меры этого события, а не от его положения, то говорят, что на этом пространстве определена геометрическая вероятность. При этом вероятность каждого события А есть отношение меры А к мере U пространства элементарных событий. Под мерой понимается

-в одномерном пространстве - длина

-в двумерном пространстве - площадь

-в трехмерном пространстве - объем

Таким образом, геометрическая вероятность означает, что

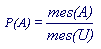
Действия над событиями

1. Если при всяком испытании, при котором происходит событие А, происходит и событие B, то событие А называется частным случаем события B.
А М B или B Й A

2. Событие (А и B), т. е. событие, состоящее в наступлении обоих событий А и B, называется произведением событий А и B и обозначается через

АB

3. Событие (А или B), т. е. событие, состоящее в наступлении хотя бы одного из событий А и B, называется суммой событий А и B и обозначается через

А + B

4. Событие, состоящее в том, что событие А не происходит, называется противоположным событию А и обозначает- ся через .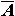
5. Событие (А и 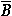), состоящее в том, что A происходит, а B не происходит, называется разностью событий А и B и обозначается через

А - B

Формула полной вероятности

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,

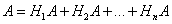
Применяя аксиому сложения вероятностей, имеем

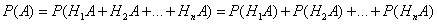
Но 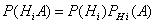(i=1, 2, ..., n), поэтому

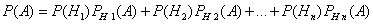Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».

Формула Байеса

Пусть событие 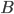происходит одновременно с одним из 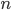несовместных событий 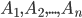. Требуется найти вероятность события 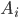, если известно, что событие 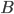произошло.

На основании теоремы о вероятности произведения двух событий можно написать

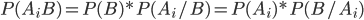
Откуда

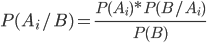
или

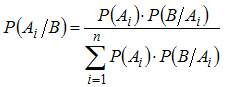(3.2)

Формула (3.2) носит название формулы Байеса.

Формулы Бернулли

Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность Pk,n того, что событие A наступит k раз в n независимых испытаниях, равна: 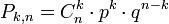где q = 1-p

Теорема Пуассона

При большом количестве испытаний вычисления по формуле Бернулли становятся затруднительными. Однако в ряде случаев их можно заменить более простыми асимптотическими формулами. Одна из них основана на теореме Пуассона.

Если число испытани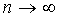й и 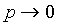так, ч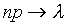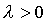то , , то 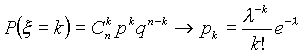при любых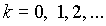

Это означает, что при больших nи малых p вместо вычислений по точной формуле

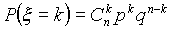
можно воспользоваться приближенной формулой ,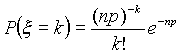

т.е. использовать формулу Пуассона для  =np.

Понятие случайной величины

Примеры дискретных случайных величин

Распределение Бернулли (или биномиальное распределение) определяется как закон распределения случайной величины, равной числу успехов в n испытаниях Бернулли. Эта случайная величина x может принять любое из значений 0, 1, 2, …, n, а их вероятности определяются формулой Бернулли: если p – вероятность успеха, q – вероятность неудачи, то

,

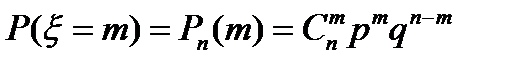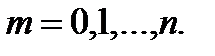
Распределение Пуассона. Случайная величина, распределенная по закону Пуассона, может принять любое из значений 0, 1, 2, … (счетное множество значений), а их вероятности задаются формулой

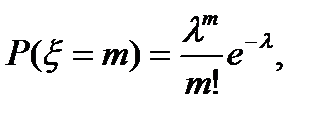
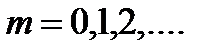, l>0.

Геометрическое распределение имеет случайная величина x, равная числу испытаний Бернулли до первого «успеха» (включительно) с вероятностью «успеха» в одном испытании равном р. Такая случайная величина принимает значения x=1, 2, 3,…, а их вероятности задаются формулой:

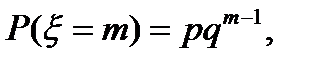
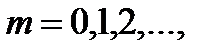
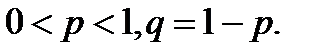
Гипергеометрическое распределение определяется, например, в задаче о выборке деталей. Пусть имеется N деталей, из которых M – стандартные. Делается выборка из n деталей. Случайная величина x определяется как число стандартных деталей в такой выборке. Оно может равняться любому числу от 0 до n, но, конечно, не больше, чем М, т.е. m=0,1,2,…,min(n,M). Вероятности этих значений определяются гипергеометрической формулой

,

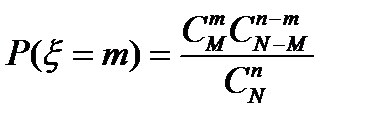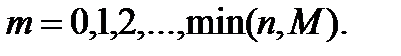
Функция распределения

Каждая случайная величина полностью определяется своей функцией распределения.

Если x .- случайная величина, то функция F(x) = Fx (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.

Функция распределения любой случайной величины обладает следующими свойствами:

1) F(x) определена на всей числовой прямой R;

2) F(x) не убывает, т.е. если x1 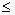x2, то F(x1) 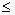F(x2);

3) F(- 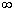)=0, F(+ 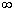)=1, т.е. 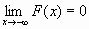и ;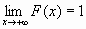

4) F(x) непрерывна справа, т.е.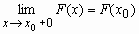

Плотность распределения

Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f (x) = F′(x).

Вероятность того,что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а,b), определяется равенством: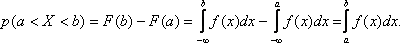

Зная плотность распределения, можно найти функцию распределения F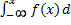(x)= x

Плотность распределения обладает следующими свойствами:

Свойство 1. Плотность распределения неотрицательна, т.е. f(x) ≥0

Свойство 2. Несобственный интеграл от плотности распределения в пределах от - 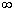до + 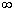равен единице: .

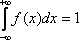В частности, если все возможные значения случайной величины принадлежат интервалу (a,b), то 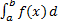x=1

Математическое ожидание ДСВ

Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.

X			…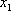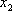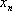
P			…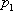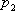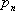

Т.е., если сл. величина имеет закон распределения, то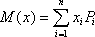

называется её математическим ожиданием. Если сл. величина имеет бесконечное число значений, то математическое ожидание определяется суммой бесконечного ряда 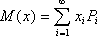, при условии, что этот ряд абсолютно сходится (в противном случае говорят, что математическое ожидание не существует).

Дисперсия ДСВ

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

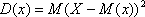
Для вычисления дисперсии можно использовать слегка преобразованную формулу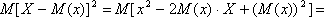

т.к. М(х), 2 и 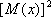постоянные величины, то

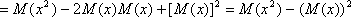
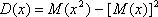
Свойства дисперсии

Свойство 1. Дисперсия постоянной равна нулю. По определению

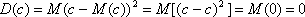
Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.

Доказательство: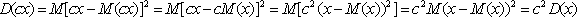

Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания.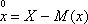

Центрированная величина обладает двумя удобными для преобразования свойствами: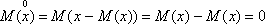

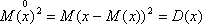
Свойство 3. Если случайные величины Х и У независимы, то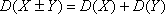

Непрерывные случайные величины (НСВ), их числовые характеристики

Случайную величину назовем непрерывной, если ее функция распределения непрерывна.

Легко видеть, что случайная величина непрерывна тогда и только тогда, когда 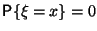при всех 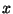. Важный класс непрерывных случайных величин - абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.

Примеры распределения НСВ

Равномерное распределение

Непрерывная случайная величина x , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения p_x (x) и функция распределения F_x (x ) имеют соответственно вид:

, .

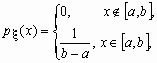
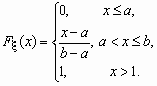
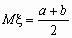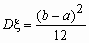Экспоненциальное (показательное) распределение

Непрерывная случайная величина x имеет показательное распределение с параметром l > 0, если она принимает только неотрицательные значения, а ее плотность распределения p_x (x )и функция распределения F_x (x) имеют соответственно вид:

, .

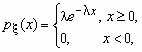
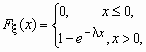
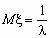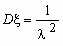Нормальное распределение

Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.

Случайная величина x нормально распределена с параметрами a и s , s >0, если ее плотность распределения p_x (x ) и функция распределения F_x (x) имеют соответственно вид:

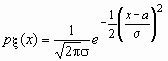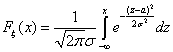, , Mx = a, Dx = s ²_.

Закон больших чисел

Закон больших чиселв теории вероятностейутверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Неравенство Чебышёва

Неравенство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего.

Теорема Бернулли

Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность P_k,n того, что событие A наступит k раз в n независимых испытаниях, равна: 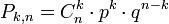где q = 1-p.

Теорема Ляпунова

Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Пусть 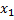, , 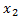…, , …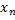- неограниченная последовательность независимых случайных величин с математическими ожиданиями 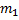, , 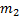…, , … 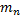и дисперсиями 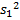, , 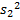…, … 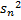. Обозначим , , ,.

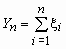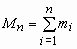
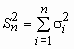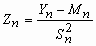Тогда 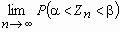= Ф(b) - Ф(a) для любых действительных чисел a и b , где Ф(x) - функция распределения нормального закона.

Тема 1. Выборочный метод

Раздел 1. Теория вероятностей

Тема 1. Случайные события

Предмет теории вероятностей

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Опыт-это явление, происходящее при условиях, созданных человеком и которое может повторяться большое кол. раз. Результатом опыта наз. случайным событием.

Виды случайных событий:

1.достоверные Е(событие, кот. в усл. данного опыта обязательно происходит)

2.невозможное U(никогда не происходят в усл. данного опыта)

3.несовместные(если в усл данного опыта не происх. одновременно)

4.совместные(в условиях данного опыта м. появиться одновременно)

5.В благопрепятствует А,если из факта появленияВ вытекает факт появления А.

6.А и Ас чертой,к каждому событию А мож. сопоставить противопол. события, т.е такое событие, кот дополн А)

1.1.2.Вероятность события.

Вероятность события — это отношение количества тех наблюдений, при которых рассматриваемое событие наступило, к общему количеству наблюдений.

n-опыт

m,a-число опытов,при кот.события происх.

M(A)/n=ω(A)-частота проведения опытов