Гамма-функция и ее свойства.
Определение 1. Несобственный интеграл
 , (1)
, (1)
где  , называется эйлеровым интегралом 2-ого рода, а функция
, называется эйлеровым интегралом 2-ого рода, а функция  переменной z называется гамма-функцией Эйлера. При этом функция
переменной z называется гамма-функцией Эйлера. При этом функция
 (2)
(2)
называется неполной гамма-функцией.
Замечание.Проинтегрируем по частям интеграл (1)

 .
.
Таким образом
 . (3)
. (3)
Т. к.  , то из формулы (3) следует:
, то из формулы (3) следует:  ,
, 
 …
… 
Таким образом  (4)
(4)
Еще одно соотношение для функции  :
:
 . (5)
. (5)
Поэтому при  получим:
получим:
 .
.
Далее, используя формулу (3), получим:

 .
.
То есть 
 . (6)
. (6)
Замечание.Перепишем формулу (3) в виде
 , (7)
, (7)
что позволяет доопределить функцию  для отрицательных значений z.
для отрицательных значений z.

Рис.1 График функции Г(z).
Пример 1.Найти  .
.
Решение.По формуле (6):
 =
=  .
.
Упражнения
6.1. Вычислить 1)  ; 2)
; 2)  , если а)
, если а)  ; б)
; б)  .
.
6.2.Проверить справедливость формулы
 при
при  .
.
6.3.Вычислить а)  , б)
, б)  , и)
, и)  .
.
Ответ:а) – 1; б) 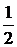 ; в)
; в)  .
.
Некоторые законы распределения времени наработки на отказ.
7.1.Экспоненциальный закон  . Подробно рассмотрен в §§ 2, 3.
. Подробно рассмотрен в §§ 2, 3.
 .
.



Рис. 2. Графики  для
для  .
.
7.2. Нормальный закон  . Подробно рассмотрен в §§ 2, 3.
. Подробно рассмотрен в §§ 2, 3.
 ,
, 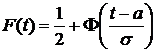 ,
,
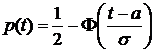 ;
;  ;
;  .
.



Рис. 3. Графики  для распределения
для распределения  .
.
7.3.Распределение Рэлея  .
.
Определение 1. Случайная величина Т называется распределенной по закону Рэлея  , если ее функция распределения
, если ее функция распределения
 – параметр распределения. (1)
– параметр распределения. (1)
Замечание.  – функция надежности, (2)
– функция надежности, (2)
 – функция плотности распределения вероятностей, (3)
– функция плотности распределения вероятностей, (3)
 – функция интенсивности отказов. (4)
– функция интенсивности отказов. (4)



Рис. 4. Графики  для
для  .
.
График 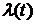 в распределении
в распределении  прямо пропорционально зависит от t. Поэтому этот закон применяют для исследования систем с ярко выраженным эффектом старения.
прямо пропорционально зависит от t. Поэтому этот закон применяют для исследования систем с ярко выраженным эффектом старения.
Так как  , то точка локального максимума для функции
, то точка локального максимума для функции 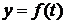
 будет точкой перегиба для функции
будет точкой перегиба для функции  .
.
Найдем еще  и
и  . По формуле (9) § 3
. По формуле (9) § 3

 , так как
, так как
 - интеграл Пуассона.
- интеграл Пуассона.
Таким образом  . (5)
. (5)
По формуле (10) § 3


 .
.
Таким образом  . (6)
. (6)
Пример 1.Время Т наработки системы на отказ распределено по закону  . При этом интенсивность отказов
. При этом интенсивность отказов 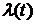 при t=1000 час равна:
при t=1000 час равна:  .
.
Найти: 1) вероятность безотказной работы системы в течение 500 час;
2)  ;
;
3)  .
.
Решение. 
 . Тогда 1)
. Тогда 1)  .
.
2) 

3) 
 час.
час.
7.4.Распределение Вейбулла.
Определение 2. Случайная величина Т называется распределенной по закону Вейбулла  , если ее функция распределения
, если ее функция распределения
 - (7)
- (7)
параметры распределения,  .
.
Замечание.  - функция надежности, (8)
- функция надежности, (8)
 - (9)
- (9)
функция плотности распределения вероятностей,
 - функция интенсивности отказов. (10)
- функция интенсивности отказов. (10)
При  становится экспоненциальным распределением
становится экспоненциальным распределением  .
.
При  становится распределением Рэлея
становится распределением Рэлея  .
.



Рис. 5. Графики  для распределения
для распределения  .
.



Рис. 6. Графики  для распределения
для распределения  .
.



Рис. 7. Графики  для распределения
для распределения  .
.
Найдем М(Т) и D(Т)

 .
.
Таким образом  . (11)
. (11)



 .
.
Таким образом  . (12)
. (12)
Пример 2.Время Т наработки системы на отказ распределено по закону Вейбулла  . При этом интенсивность отказов
. При этом интенсивность отказов 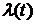 в момент времени t=1000 час равна
в момент времени t=1000 час равна  . Найти :
. Найти :
1) вероятность безотказной работы за это время.
2)  .
.
Решение.1) По Формуле (10):
 ;
;  ;
;
 .
.
По формуле (8):  .
.
 .
.
2) По формуле (11): 
 .
.
Так как  , то
, то  и
и
 час.
час.
Упражнения.
7.1. Нерезервированная невосстанавливаемая система состоит из 3-х последовательно соединенных элементов. Время жизни элементов распределено по закону Рэлея:  . Определить показатели надежности системы:
. Определить показатели надежности системы:  . Определить время, в течение которого система будет исправна с вероятностью
. Определить время, в течение которого система будет исправна с вероятностью  .
.
Ответ.  ,
,  .
.
7.2.Нерезервированная система состоит из n последовательно соединенных элементов, время жизни которых  . 1) Найти показатели надежности системы. 2) Определить по какому закону распределено время жизни системы.
. 1) Найти показатели надежности системы. 2) Определить по какому закону распределено время жизни системы.
Ответ.1) 
 ;
;  .
.
2)  .
.
7.3. Резервированная невосстанавливаемая система состоит из 2-х параллельно соединенных элементов (постоянно включенный резерв). Время жизни каждого элемента  . Определить показатели надежности системы:
. Определить показатели надежности системы:  . Определить
. Определить  для одного элемента.
для одного элемента.
Ответ.  ,
,
Тср(для одного элемента) = 177 час.
7.4.Время Т наработки элемента на отказ распределено по закону Вейбулла  . При этом интенсивность отказов
. При этом интенсивность отказов 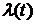 :
:  . Найти :
. Найти :
1) Найти параметры  .
.
2) Найти показатели надежности при t=2000 час.
3)  , D(T).
, D(T).
Ответ.1)  ,
,  ; 3)
; 3)  ,
,  .
.
7.5. Нерезервированная система состоит из 8 последевательно соединенных элементов, время жизни которых распределено по закону  . Определить по какому закону распределено время жизни системы.
. Определить по какому закону распределено время жизни системы.
Ответ.  .
.
7.6.Время Т наработки детали на отказ распределено по закону Рэлея  . Найти показатели надежности работы детали
. Найти показатели надежности работы детали  при а) t=10000 час, б) t=20000 час. Найти
при а) t=10000 час, б) t=20000 час. Найти  , D(T).
, D(T).
7.7.Время Т наработки системы на отказ распределено по закону  , при этом интенсивность отказов
, при этом интенсивность отказов 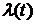 при t=5000 час равна:
при t=5000 час равна:  . Найти 1) параметр
. Найти 1) параметр 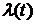 ; 2)
; 2)  , D(T); 3) показатели надежности работы системы
, D(T); 3) показатели надежности работы системы  а) через год, б) через 2 года ( считать, что в году 8760 час).
а) через год, б) через 2 года ( считать, что в году 8760 час).
7.8.Нерезервированная система состоит из 2-х последовательно соединенных элементов. Время жизни 1-ого элемента распределено по закону  , 2-ого -
, 2-ого -  . Найти 1) показатели надежности системы, 2)
. Найти 1) показатели надежности системы, 2)  .
.
7.9.Время Т наработки элемента на отказ распределено по закону Вейбулла  . При этом интенсивность отказов
. При этом интенсивность отказов  .
.
1) Найти параметр  .
.
2) Найти показатели надежности через t=2000 час.
3)  .
.
Ответ.  ,
,  ;
;  .
.
7.10.Время Т наработки устройства на отказ распределено по закону  . Найти Тср , D(T), показатели надежности через t=2000 час.
. Найти Тср , D(T), показатели надежности через t=2000 час.
Ответ.  ;
;  ,
,  ;
;  ,
,
Гамма - распределение.
Определение 1. Случайная величина Т имеет гамма – распределение  , если ее функция распределения
, если ее функция распределения
 , (1)
, (1)
где  – неполная гамма – функция (см. §6),
– неполная гамма – функция (см. §6),  – параметры распределения;
– параметры распределения;  .
.
Замечание. 
 . Таким образом,
. Таким образом,  – (2)
– (2)
функция плотности вероятностей,

 – (3)
– (3)
функция надежности,

 – (4)
– (4)
функция интенсивности отказов.
Из формулы (2) видно, что для 
 и , следовательно, распределение
и , следовательно, распределение  совпадает с
совпадает с  .
.



Рис.1 Графики  для распределения Г(5;1/300).
для распределения Г(5;1/300).



Рис.2 Графики  для распределения Г(1/2;1/3000).
для распределения Г(1/2;1/3000).
Найдем еще 


 .
.
Таким образом  . (5)
. (5)

 (по формуле (3) § 6)
(по формуле (3) § 6)
 .
.
Таким образом
 . (6)
. (6)
Большой интерес представляет случай, когда в распределении  параметр
параметр  – натуральное число ,
– натуральное число ,  .
.
Определение 2. Пусть  , тогда распределение
, тогда распределение  называется распределением Эрланга порядка k.
называется распределением Эрланга порядка k.
Замечание.Так как  , то из формулы (3) следует:
, то из формулы (3) следует:

 =
=  –
– 
 .
.
И далее, если проводить интегрирование по частям еще (k-2) раз, то получим

 . (7)
. (7)
Случайная величина Т, распределенная по закону Эрланга  возникает при рассмотрении модели накапливающихся повреждений: если через случайные интервалы времени в системе возникают единичные повреждения, вызванные потоком случайных событий, и при накоплении k повреждений система отказывает. Тогда, если время между наступлением 2-х последовательных событий потока распределено по показательному закону
возникает при рассмотрении модели накапливающихся повреждений: если через случайные интервалы времени в системе возникают единичные повреждения, вызванные потоком случайных событий, и при накоплении k повреждений система отказывает. Тогда, если время между наступлением 2-х последовательных событий потока распределено по показательному закону  , то Т – время наработки системы на отказ распределена по закону
, то Т – время наработки системы на отказ распределена по закону  .
.
Действительно, верна теорема:
Теорема 1. Пусть время между наступлением 2-х соседних событий потока (время между 2-мя единичными повреждениями) распределено по закону  . Тогда случайная величина Y – число событий потока за время t (число случайных повреждений системы) распределено по закону Пуассона
. Тогда случайная величина Y – число событий потока за время t (число случайных повреждений системы) распределено по закону Пуассона  , т.е.
, т.е.  .
.
Подробнее о потоках случайных событий см. § 14.
Из теоремы 1 следует, что для рассмотренной выше СВ Т – времени жизни системы, функция надежности

 ,
,
что совпадает с формулой (7).
Замечание.Для системы рассмотренной выше последовательность моментов времени наступления единичных повреждений можно представить в виде:
 - время наработки системы на отказ, причем Ti независимы и имеют распределение
- время наработки системы на отказ, причем Ti независимы и имеют распределение  ,
,  .
.
Пример 1.Время жизни изделия Т распределено по закону  , причем
, причем  час. Найти показатели надежности изделия через 4000 час.
час. Найти показатели надежности изделия через 4000 час.
Решение.
 .
.
Тогда, по формуле (7)
 .
.
 .
.
 .
.
Упражнения.
10.1. Время Т наработки устройства на отказ распределено по закону:  .
.
1) Записать функции:  .
.
2) Найти Тср , D(T).
3) Найти показатели надежности при  час.
час.
Ответ.
10.2. Время Т жизни элемента распределено по закону  .
.
1) Найти показатели надежности при  час.
час.
2) Найти Тср , D(T).
Ответ.  час2.
час2.
10.3. а) Дана резервированная система (резерв замещением кратности m=2):

Время жизни каждого элемента распределено по закону  :
:
1) Определить по какому закону распределено Т – время жизни системы, записать функцию p(t).
2) Найти Тср .
б) Дана резервированная система ( постоянно включенный резерв кратности m=2):

Время жизни каждого элемента распределено по закону  :
:
1) Записать функцию p(t) для Т – времени жизни системы.
2) Найти Тср .
10.4. Дана резервированная система (резерв замещением кратности m=3).
 Время жизни каждого элемента распределено по закону
Время жизни каждого элемента распределено по закону  :
:
0. у.
а) Определить по какому закону распределено Т – время жизни системы.
б) Найти показатели надежности.
в) Найти Тср , D(T).
Ответ. а)  .
.
Приложение 2. РГР Законы распределения времени наработки на отказ.
Постановка задачи
Система состоит из трех последовательно соединенных элементов, законы распределения времени наработки на отказ которых приведены в таблице. Найти показатели надежности каждого элемента и всей системы в целом:
1. Среднее время жизни , среднее квадратическое отклонение  для каждого элемента, где
для каждого элемента, где  - время наработки на отказ.
- время наработки на отказ.
2. Функцию плотности вероятностей для случайной величины  .
.
3. Функцию надежности.
4. Функцию интенсивности отказов.
5. Построить графики  .
.
6. Протабулировать функции  .
.
7. Среднее время жизни системы.
Задания
| В1 | В2 | В3 | В4 | В5 | |
| 1-й элемент | W(2;1/1500) | R(1/1000) | W(1;1/2000) | W(3;1/3000) | W(4;1/2000) |
| 2-й элемент | Г(8;1/200) | Exp(1/1000) | Г(5;1/500) | Г(7;1/1000) | W(1;1/1500) |
| 3-й элемент | TN(1500;800) | TN(3000;300) | TN(1000;700) | TN(1000;800) | TN(100;800) |
| В6 | В7 | В8 | В9 | В10 | |
| 1-й элемент | W(4;1/3000) | R(1/2000) | W(5;1/3000) | Г(5;1/800) | W(6;1/3000) |
| 2-й элемент | Г(6;1/800) | Г(6;1/800) | Г(6;1/1000) | Г(5;1/800) | W(6;1/3000) |
| 3-й элемент | TN(0;1000) | TN(200;800) | R(1/3000) | Exp(1/2000) | TN(500;1000) |
| В11 | В12 | В13 | В14 | В15 | |
| 1-й элемент | W(5;1/2000) | R(1/1500) | W(1/5;1/3) | R(1/1600) | W(4;1/1800) |
| 2-й элемент | TN(600;1000) | Г(7;1/1500) | Г(7;1/200) | R(1/1600) | W(1;1/1400) |
| 3-й элемент | TN(600;1000) | TN(700;1000) | TN(700;1000) | TN(800;1000) | TN(150;800) |
| В16 | В17 | В18 | В19 | В20 | |
| 1-й элемент | W(2;1/1600) | R(1/1200) | W(1;1/2200) | W(3;1/3200) | W(4;1/2300) |
| 2-й элемент | Г(8;1/250) | Exp(1/1200) | Г(5;1/550) | Г(7;1/1200) | W(1;1/1600) |
| 3-й элемент | TN(1400;800) | TN(2500;300) | TN(900;700) | TN(1200;800) | TN(350;800) |
| В21 | В22 | В23 | В24 | В25 | |
| 1-й элемент | W(4;1/3100) | R(1/2200) | W(5;1/3100) | Г(5;1/850) | W(6;1/3200) |
| 2-й элемент | Г(6;1/900) | Г(6;1/900) | Г(6;1/1100) | Г(5;1/850) | W(6;1/3200) |
| 3-й элемент | TN(0;1200) | TN(200;850) | R(1/3100) | Exp(1/2200) | TN(500;1200) |
| В26 | В27 | В28 | В29 | В30 | |
| 1-й элемент | W(5;1/2100) | R(1/1600) | W(1/5;1/3) | R(1/1700) | W(4;1/1900) |
| 2-й элемент | TN(600;1100) | Г(7;1/1600) | Г(7;1/220) | R(1/1700) | W(1;1/1500) |
| 3-й элемент | TN(600;1100) | TN(700;1300) | TN(700;1100) | TN(800;1200) | TN(250;800) |
Пример решения в среде Mathematica.
Текстовая ячейка Subsubtitle Законы распределения времени наработки на отказ элементов:  |
| Текстовая ячейка Subtitle Показатели надежности для W(aa,ll) |
Группа ячеек ввода aa:= 2 ll:=1/2000 MT:=Gamma[1+1/aa]/ll sT:=Sqrt[(Gamma[1+2/aa]-(Gamma[1+1/aa])^2)]/ll Labeled[N[MT],Среднее время жизни,Left] Labeled[N[sT],Среднее квадратическое отклонение, Left] f1= aa*(ll^aa)*(x^(aa-1))*Exp[-((ll*x)^aa)] p1=Exp[-((ll*x)^aa)] lam1=aa*(ll^aa)*(x^(aa-1)) Plot[f1,{x,0,5000}, PlotLabel "Плотность вероятностей"] Plot[p1,{x,0,5000},PlotLabel "Функция надежности "] Plot[lam1,{x,0,5000}, PlotLabel "Интенсивность отказов"] ------Ячейки вывода --------------------------- Время жизни Среднее 1772.45 Среднее отклонение квадратическое 926.503       |
| Текстовая ячейка Subtitle Показатели надежности для Г(a,l) |
Группа ячеек ввода l:=1/300 a:=5 Labeled[a/l, Среднее время жизни,Left] Labeled[N[Sqrt[a]/l], Среднее квадратическое отклонение, Left] f2=(l^a)*(x^(a-1))*Exp[-l*x]/Gamma[a] p2=Gamma[a,l*x]/Gamma[a] lam2=((l^a)*(x^(a-1))*Exp[-l*x])/(Gamma[a,l*x]) Plot[f2,{x,0,5000}, PlotLabel "Плотность вероятностей"] Plot[p2,{x,0,5000},PlotLabel "Функция надежности "] Plot[lam2,{x,0,5000}, PlotLabel "Интенсивность отказов"] ------Ячейки вывода --------------------------- Время жизни Среднее 1500 Среднее отклонение квадратическое 670.82       |
Текстовая ячейка Subtitle Показатели надежности для TN(aaa,s), функция Лапласа  . . |
Группа ячеек ввода aaa:= 2000 s:= 1000 xx:=aaa/s c=1/(0.5+0.5*Erf[0,xx/Sqrt[2]]) k=(c/Sqrt[2*Pi])*Exp[-(xx^2)/2] Labeled[N[aaa+k*s], Среднее время жизни ,Left] Labeled[N[s*Sqrt[1+k*xx-k^2]], Среднее квадратическое отклонение , Left] f3=c*PDF[NormalDistribution[aaa,s],x] p3=c*(0.5-0.5*Erf[0,(x-aaa)/(s*Sqrt[2])]) lam3=c*PDF[NormalDistribution[aaa,s],x]/p3 Plot[f3,{x,0,5000}, PlotLabel "Плотность вероятностей"] Plot[p3,{x,0,5000},PlotLabel "Функция надежности "] Plot[lam3,{x,0,5000}, PlotLabel "Интенсивность отказов"] ------Ячейки вывода --------------------------- 1.02328 0.0552479 Время жизни Среднее 2055.25 Среднее отклонение квадратическое 1052.35       |
| Текстовая ячейка Subtitle Функция надежности системы |
Группа ячеек ввода p= p1*p2*p3 Plot[p,{x,0,5000},PlotLabel® "Функция надежности системы "] ------Ячейки вывода ---------------------------   |
| Текстовая ячейка Subtitle Интенсивность отказа системы |
Группа ячеек ввода lam=lam1+lam2+lam3 Plot[lam,{x,0,5000}, PlotLabel® " Интенсивность отказов системы"] ------Ячейки вывода ---------------------------   |
| Текстовая ячейка Subtitle Плотность распределения вероятностей системы |
Группа ячеек ввода f:= p*lam Plot[f,{x,0,5000}, PlotLabel "Плотность распределения времени наработки на отказ системы"] ------Ячейки вывода ---------------------------  |
| Текстовая ячейка Subtitle Таблица значений функций p(i), i=1,…,3 и p с шагом 100 час |
Группа ячеек ввода MatrixForm[Table[{x,N[p1,6],N[p2,6],N[p3,6],N[p,6]},{x,0,3000,100}]] ------Ячейки вывода ---------------------------  |
| Текстовая ячейка Subtitle Таблица значений функций f(i), i=1,…,3 и f с шагом 100 час |
Группа ячеек ввода MatrixForm[Table[{x,N[f1,6],N[f2,6],N[f3,6],N[f,6]},{x,0, 3000,100}]] ------Ячейки вывода ---------------------------  |
| Текстовая ячейка Subtitle Среднее время жизни системы |
Группа ячеек ввода  ------Ячейки вывода --------------------------- ------Ячейки вывода ---------------------------  |
ЛИТЕРАТУРА
1. А.М. Половко, С.В. Гуров. Основы теории надежности. С. – Петербург, БХВ – Петербург, 2008.
2. А.М. Половко, С.В. Гуров. Основы теории надежности. Практикум. С. – Петербург, БХВ – Петербург, 2006.
3. В.К. Саульев. Математическая теория надежности и восстановления. – Москва, МАИ, 1974.
4. Н.П. Ямпурин, А.В. Баранова. Основы надежности электронных средств. – Москва, Изд. центр «Академия», 2010.
5. Т.А.Голинкевич. Прикладная теория надежности. – М. Высшая школа, 1977.
6. Г.Н. Черкасов. Надежность аппаратно-программных комплексов. Учебное пособие. – СП.б.: Питер, 2005.
7. А.М. Половко. Mathematica для студента. – СП.б.: БХВ – Петербург, 2007.
СОДЕРЖАНИЕ
§ 1. Вероятностное пространство. 3
Упражнения. 6
§ 2. Случайные величины. 8
§ 3. Основные понятия теории надежности. 14
§ 4. Статистическое оценивание показателей надежности. 20
§ 5. Показатели надежности для сложных систем. 24
§ 6. Гамма-функция и ее свойства. 36
§ 7. Некоторые законы распределения времени наработки на отказ. 37
§ 8. Усеченное нормальное распределение. 46
§ 9. Логарифмическое нормальное распределение. 49
§ 10. Гамма - распределение. 51
§ 11. Распределение  . 56
. 56
§ 12. Случайные процессы. 60
§ 13. Цепи Маркова. 62
§ 14. Потоки событий. 71
§ 15. Марковcкие процессы с дискретными состояниями и непрерывным временем. 73
Приложение 1. Вычисления в среде Mathematica. 89
Приложение 2. РГР Законы распределения времени наработки на отказ. 95
ЛИТЕРАТУРА.. 106
Учебное издание
ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ ТИПОВЫХ РАСЧЕТОВ
ПО МАТЕМАТИКЕ
для студентов 1 курса
энергетического факультета
Составители:
РУДЫЙ Александр Никодимович
Редактор Т.Н. Микулик
_____________________________________________________________
Подписано в печать .2009.
Формат 60×84  . Бумага офсетная.
. Бумага офсетная.
Отпечатано на ризографе. Гарнитура Таймс.
Усл. печ. л. 5,81. Уч.-изд. л. 2,27. Тираж . Заказ .
____________________________________________________________
Издатель и полиграфическое исполнение:
Белорусский национальный технический университет.
ЛИ № 02330/0131627 от 01.04.2004.
Проспект Независимости, 65, 220013, Минск.
