В дальнейшем нам потребуется интеграл Пуассона

.

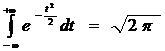Используя этот интеграл несложно заметить, что функция распределения f(x) удовлетворяет основному соотношению

.

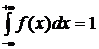Действительно, обозначив 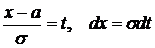, можно написать

.

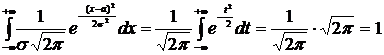Числовые характеристики нормального распределения. Определим математическое ожидание случайной величины с нормальным законом распределения

.

.

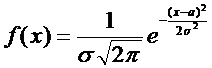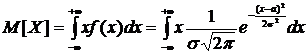Выполнив замену переменной 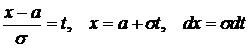, получаем

.

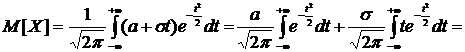
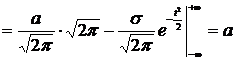Итак, М[X]=a. Значение параметра а в формуле, определяющей плотность распределения вероятности, равно математическому ожиданию рассматриваемой случайной величины. Точка х=а является центром распределения вероятностей, или центром рассеивания.

Найдем

.

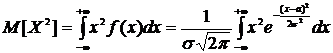Выполнив ту же замену переменной, будем иметь

.

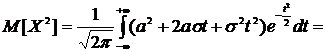
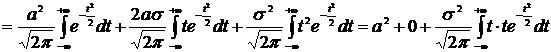Проинтегрировав по частям последний интеграл: u=t, 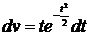, получим

.

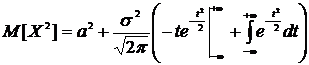Так как по правилу Лопиталя 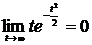, то

.

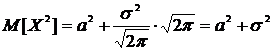Поэтому дисперсия нормального распределения случайной величины будет

.

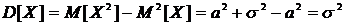Итак, M[X]=a, D[X]=σ², σ[X]= σ.

7. Функция Лапласа. Функция распределения случайной величины Х, имеющей нормальное распределение.В дальнейшем будем использовать функцию Лапласа, определяемую равенством

.

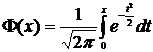Составлены подробные таблицы значений этой функции.

Укажем некоторые свойства функции Ф(х).

1. Ф(х) определена при всех значениях х.

2. Ф(0)=0.

3. .

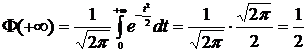4. .

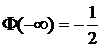5. Ф(х) монотонно возрастает при всех .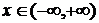

6. Ф(х) – функция нечетная: Ф(-х)= - Ф(х).

Определим функцию распределения случайной величины Х, имеющей нормальное распределение.

.

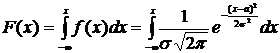Обозначив 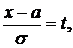получим

.

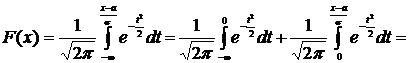
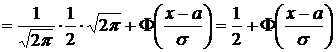Итак, функция распределения случайной величины Х имеет вид

.

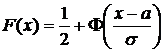8. Вероятность попадания случайной величины Х, имеющей нормальное распределение, в заданном интервале.Используя функцию распределения случайной величины Х, найдем вероятность попадания ее значений в интервал (α, β).

.

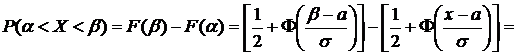
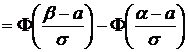Таким образом, .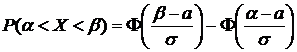

Пример. Найти вероятность попадания в интервал 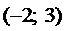для нормально распределенной случайной величины с параметрами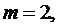

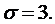
Имеем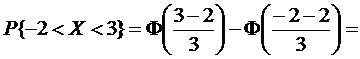

◄

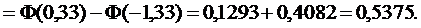Известно («правило трех сигм»), что практически все возможные значения нормально распределенной случайной величины сосредоточены в интервале 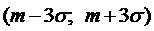. Действительно, вероятность попадания в этот интервал равна 0,9973, то есть выход за его границы можно считать событием практически невозможным ( ).

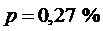Пример. Найти математическое ожидание и дисперсию нормально распределенной случайной величины, принимающей значения от 3,5 до 10,1.

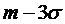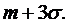Будем считать границы интервала равными и Тогда 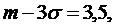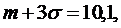и следовательно, ◄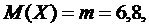

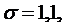
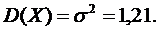Пример.Непрерывная случайная величина распределена нормально с 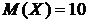, 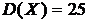. Найти интервал, в котором согласно правилу «трех сигм» попадает случайная величина с вероятностью 0,9973.

Правило «трех сигм» представлено формулой

.

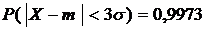Так как 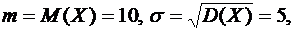то

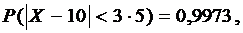откуда .

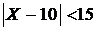Решая последнее неравенство, получаем

,

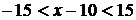откуда .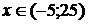

Пример. Плотность распределения вероятностей случайной величины Х имеет вид 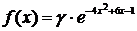. Найти: γ, M[X], D[X], F(x), .

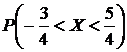Случайная величина Х имеет нормальное распределение. Поэтому приведем плотность распределения f(x) к виду

.

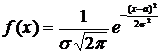Выделим в показателе заданной функции полный квадрат

.

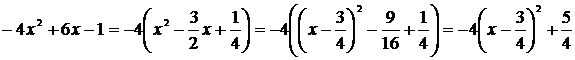Следовательно,

.

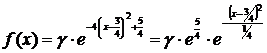Сравним

.

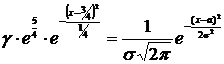Из последнего равенства получаем

.

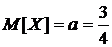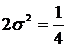, т.е. .

, .

.

.

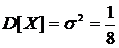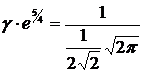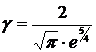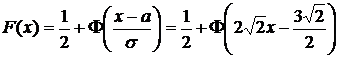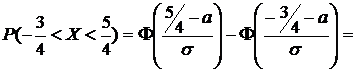
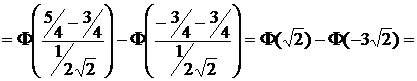
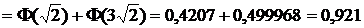В последнем равенстве при вычислени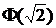и и 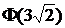использованы таблицы значений функции Ф(х).

Итак: , , , , . ◄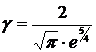

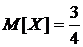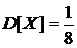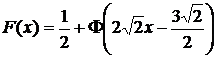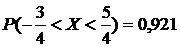Вопросы для самопроверки

1. Сформулируйте определение случайной величины.

2. Какие случайные величины называются дискретными? непрерывными? Приведите примеры тех и других случайных величин.

3. Опишите форму таблицы распределения случайной величины. Как такая таблица изображается на чертеже?

4. Дайте определение закона распределения вероятностей случайной вели­чины.

5. Как определяется дифференциальная функция распределения вероятностей случайной величины? Почему эту функцию называют функцией распределения плотности вероятности случайной величины?

6. Как вычисляется вероятность попадания в заданный интервал дискрет­ной случайной величины?

7. Дайте определение математического ожидания случайной величины. Ка­кое свойство случайной величины характеризует математическое ожидание?

8. Дайте определения дисперсии и среднего квадратического отклонения. Для характеристики какого свойства случайной величины применяют диспер­сию или среднее квадратическое отклонение?

9. Перечислите свойства математического ожидания и дисперсии.

10. Начертите форму кривой нормального распределения. Как меняется кри­вая при изменении математического ожидания и среднего квадратического от­клонения?

!1. Изложите методику расчета вероятности попадания случайной величины в заданный интервал при нормальном распределении.

12. Сформулируйте теорему Ляпунова. Объясните структуру случайных ве­личин- характеризуемых нормальным распределением.

13. Что понимается под законом больших чисел?

14. Сформулируйте теорему Бернулли. Какое значение имеет эта теорема для практики?

15. Сформулируйте теорему Чебышева. Укажите ее значение для практики.