Можно показать, что для распределения Пуассона

M[X]= D[X]=λ=np.

Непрерывные случайные

Величины

1. Функция распределения. Для непрерывной случайной величины теряет смысл понятие вероятности каждого конкретного значения, поскольку таких значений бесконечно много, и из условия, что сумма вероятностей всех значений равна 1, следует, что вероятность каждого фиксированного значения равна нулю. Поэтому основными характеристиками, описывающими поведение непрерывной случайной величины, являются функция распределения (интегральная функция распределения) и плотность распределения вероятностей (плотность вероятности, дифференциальная функция распределения).

Рассмотрим непрерывную случайную величину Х, заданную а некотором интервале (а, b). Закон распределения вероятностей для такой величины должен позволять находить вероятность попадания ее значения в любой интервал (х₁, х₂).

Функцией распределения непрерывной случайной величиныХ называют функцию F(x), определяющую для каждого значения 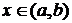вероятность того, что случайная величина Х примет значение, меньшее х, т.е. .

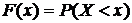Функция распределения обладает следующими свойствами:

1. Как любая вероятность .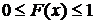

2. F(x) – неубывающая функция, т.е. если х₁< х₂, то F(x₁)≤ F(x₂).

3. .

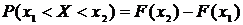4. Р(Х= x₁)=0.

5. Если все возможные значения случайной величины Х находятся на интервале (а, b), то F(x)=0 при х≤а и F(x)=1 при .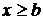

6. , .

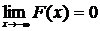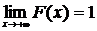Плотностью распределения непрерывной случайной величины Х называют производную от функции распределения: .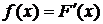

Плотность распределения непрерывной случайной величины Х обладает свойствами:

1. f(x)≥0.

2. .

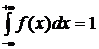3. Зная плотность распределения, можно найти функцию распределения случайной величины .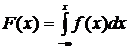

4. .

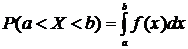График функции 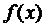называют кривой распределения.

Примеры.

1.Случайная величина Х задана функцией распределения

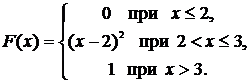
Найти плотность распределения этой случайной величины и вероятность попадания ее в интервал (1; 2,5).

По определению

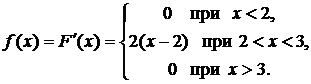
Требуемая вероятность будет

. ◄

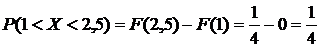2.Дана плотность распределения непрерывной случайной величины Х:

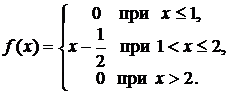
Найти функцию распределения этой величины.

Воспользуемся формулой .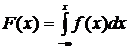

Если х≤1, то f(x)=0, следовательно, .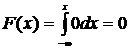

Если 1<x≤2, то

.

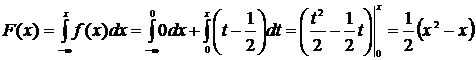Если х>2, то

.

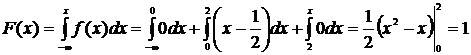Итак, искомая функция распределения имеет вид

◄

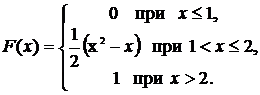3.Составить функцию распределения F(x) дискретной случайной величины Х с законом распределения:

Х
Р	0,5	0,2	0,3

Если х≤2, то F(x)=0, так как значений меньших 2 величина Х не принимает. Поэтому при х≤2 F(x)=Р(Х<x)=0.

Если 2<x≤4, то F(x)=0,5, так как Х может принимать значение 2 с вероятностью 0,5.

Если 4<x≤7, то F(x)= Р(Х<x)= Р(Х=2)+ Р(Х=4)=0,5+0,2=0,7 (по теореме сложения вероятностей несовместных событий).

Если х>7, то F(x)=1, так как событие Х≤7 достоверное.

Итак, искомая функция распределения имеет вид

◄

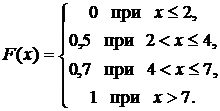2. Числовые характеристики непрерывной случайной величины. Аналогично тому, как это было сделано для дискретной случайной величины, определим числовые характеристики непрерывной случайной величины Х с плотностью распределения f(x).

Математическим ожиданием непрерывной случайной величины Х с плотностью распределения f(x) называется выражение

.

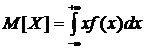Если случайная величина Х может принимать значения только на конечном отрезке [a, b], то .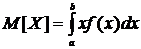

Дисперсия непрерывной случайной величины Х определяется равенством

,

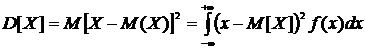или равносильным равенством

.

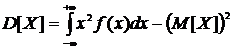Все свойства математического ожидания и дисперсии, указанные для дискретных величин, сохраняются и для непрерывных величин

Среднеквадратичным отклонением случайной величины Х называется корень квадратный из дисперсии

.

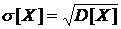Значение случайной величины Х, при котором плотность распределения f(x) имеет наибольшее значение называется модой М₀[X].

Медианой М_е[X] непрерывной случайной величины Х, называют ее значение, определяемой равенством

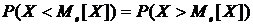
или

.

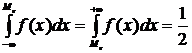Пример. Случайная величина Х задана плотностью распределения

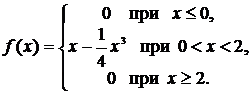
Найти математическое ожидание, дисперсию и среднеквадратичное отклонение величины Х.

Воспользуемся определениями.

.

.

.

. ◄

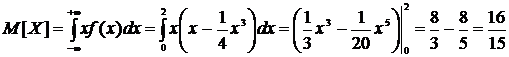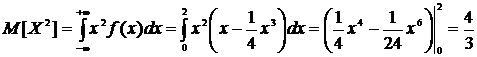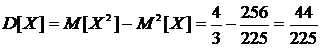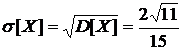Пример. Плотность вероятности случайной величины 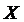имеет вид:

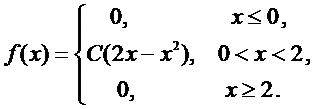
Найти:

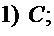
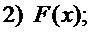
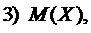
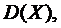
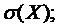
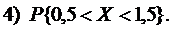
1) Из условия нормированности плотности вероятности следует, что 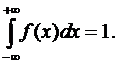В нашем случае

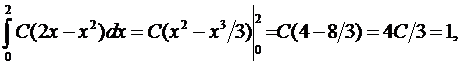
откуда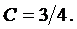

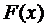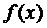2) Связь между и задается формулой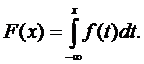

Поэтому при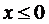

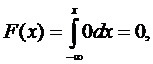
при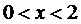

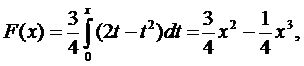
а для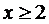

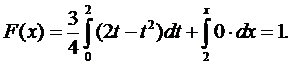
Cледовательно,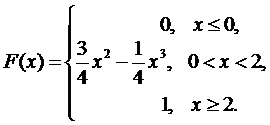

◄

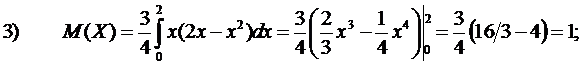
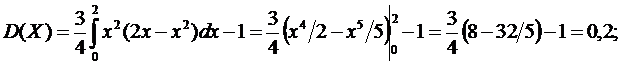
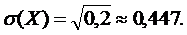
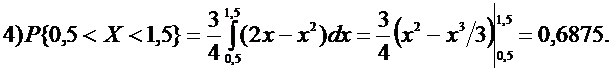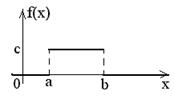3. Закон равномерного распределения вероятностей непрерывной случайной величины. Непрерывная случайная величина Х имеет равномерное распределение вероятностей если ее плотность распределения задается следующим образом:

Найдем значение с. По свойству плотностей распределения 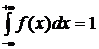получаем

,

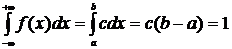следовательно, 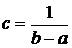и

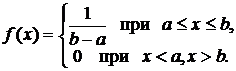
Так как 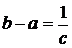, то промежуток [a, b], на котором имеет место равномерное распределение, обязательно конечен.

Определим вероятность того, что случайная величина Х примет значение, заключенное в интервале (α, β).

.

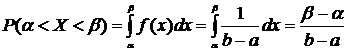Итак, искомая вероятность

,

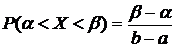т.е. вероятность попадания Х в интервал зависит только от длины этого интервала и не зависит от значений величины Х. При равномерном распределении случайной величины Х вероятности попадания Х в промежутки равной длины одинаковы.

Найдем функцию распределения .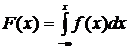

Если х<a, то f(x)=0 и, следовательно, .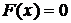

Если а≤x≤b, то 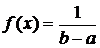и, следовательно,

.

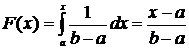Если х>b, то f(x)=0 и, следовательно,

.

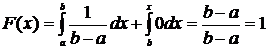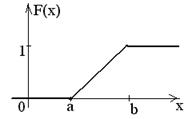
Таким образом,

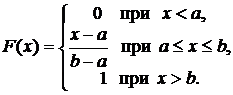
Пример. Интервал движения автобуса равен 20 минутам. Найти вероятность того, что пассажир будет ожидать автобус менее 5 минут.

Пусть случайная величина Х – время прихода пассажира на станцию после отправления очередного автобуса 0<X<20. Х имеет равномерное распределение, так как вероятность прихода, например, в пятую минуту, равна вероятности прихода в восьмую. В задаче требуется найти вероятность того, что случайная величина Х примет значение из интервала (15, 20).

. ◄

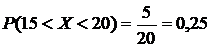4. Числовые характеристики равномерного распределения. Для случайной величины Х, имеющей равномерное распределение, плотность распределения определяется формулой

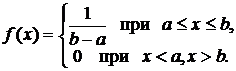
Тогда по определению математического ожидания

.

.

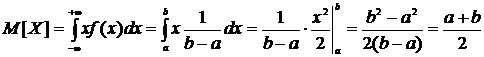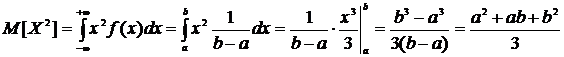Дисперсия равномерно распределенной случайной величины будет

.

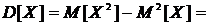
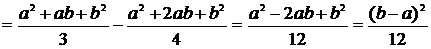Итак,

, = , .

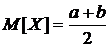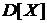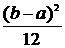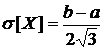5. Нормальный закон распределения непрерывной случайной величины. 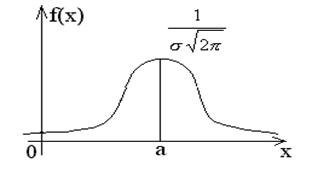Изучение различных явлений показывает, что многие случайные величины, имеют плотность распределения вероятности, которая определяется формулой

,

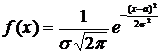где а и σ – параметры распределения. В этом случае говорят, что случайная величина Х подчинена нормальному закону распределения. Кривая нормального распределения изображена на рисунке.