Дисперсия СВ, распределенной по гипергеометрическом закону определяется как
Г) 
.
8. Согласно свойствам функции распределения F(x) данная функция:
А) неотрицательная и неубывающая
9. Вероятность попадания нормально распределенной СВ в заданный интервал вычисляется:
Б) 
;
10. Задача: в ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. При условии, что 10% счетов содержат ошибки, какому закону распределения подчиняется количество счетов с ошибками среди отобранных?
| А) биномиальному; | В) равномерному; |
| Б) гипергеометрическому; | Г) закону распределения Пуассона. |
11. Если значение коэффициента асимметрии 
, то асимметрия:
| А) существенная левосторонняя; | В) существенная правосторонняя; |
| Б) несущественная левосторонняя; | Г) несущественная правосторонняя. |
12. Если все варианты ряда уменьшить (увеличить) на постоянную величину k, то дисперсия:
| А) не измениться; |
13. Коэффициент вариации рассчитывается:
Б) 
14. . Если строится 95%-ный доверительный интервал, то в каких границах будет находиться неизвестное значение генеральной средней?
Г) 
Теоретической основой выборочного метода является
Г) теорема Чебышева (общий случай).
16. Сущность выборочного метода состоит в том, что:
А) для изучения вместо всей совокупности элементов берётся лишь некоторая их часть, отобранная по определённым правилам
17. Необходимый объем выборки для оценки генеральной средней при собственно- случайном повторном отборе может быть найден как:
А)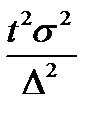 
;
18. При помощи 
- критерия Пирсона осуществляется проверка гипотезы о
А) числовом значении доли;
Б) равенстве двух генеральных средних с неизвестными дисперсиями ;
В) равенстве двух генеральных дисперсий;
Г) нормальном распределении генеральной совокупности
19. Критические области бывают:
Г)одно- или двухсторонними
20. Задача: в молочном отделе универсама произведено контрольное взвешивание десяти 200-грамовых пачек сливочного масла и установлено, что 
г. и S=4г. Менеджер отдела выдвигает предположение о недобросовестности поставщика. Прав ли он? Уровень значимости принять равным 
=0,001. Нулевая и альтернативная гипотезы формулируются как:
А)  ; | Б)  ; | В)  ; | Г)  . |
Еще одни 2011..
БИЛЕТ № 7, 22
1. Согласно свойству сочетаний:
Б)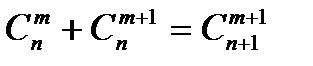 
, где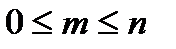 
;
| 2. | Несовместные события могут быть определены как: |
| А. | несколько событий называются несовместными, если в результате опыта наступление одного из них исключает появление других; |
3. Теорема умножения двух зависимых событий может быть записана как:
В)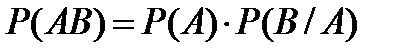 
| 4. | Правило полной вероятности утверждает: |
| А. | если событие А может наступить только вместе с одним из событий Н1, Н2, Н3,…., Нn, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н1, Н2, Н3,…., Нn, на соответствующую условную вероятность события А; |
| 5. | Случайную величину называют непрерывной если: |
она может принять любое значение из некоторого конечного или бесконечного интервала;
6. Дисперсия биномиального распределения рассчитывается как:
Б)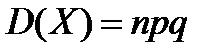 
;
7. Формула распределения вероятностей Пуассона записывается как:
Б)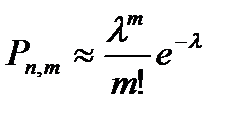 
;
8. Нормальная СВ имеет плотность распределения, определяемую формулой:
А)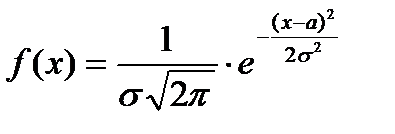 
;
9. Согласно свойствам дифференциальной функции f(x),эта функция:
А)положительная;
Задача: вероятность сдать экзамен на право вождения автомобиля одинакова для всех слушателей курсов и равна 0,8. В группе 20 человек. Какому закону распределения будет подчиняться число слушателей, получивших права?
| В) равномерному; | ||
11. Для расчета коэффициента асимметрии используется:
| А)центральный момент четвертого порядка; | В) начальный момент четвертого порядка; |
| Б) центральный момент третьего порядка; | Г) начальный момент третьего порядка. |