Случайная величина - это величина, принимающая те или иные значения в зависимости от случая.

Случайная величина называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Задание дискретной случайной величины по определению равносильно заданию закона распределения случайной величины в следующем виде:

где 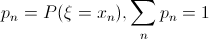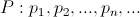Примеры дискретных случайных величин:

1) дискретная случайная величина Бернулли(закон распределения Бернулли). Закон распределения дискретной случайной величины Бернулли имеет следующий вид: 0<p<1

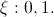
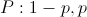Такому распределению соответствует бросание монеты, на одной стороне которой - 0, а на второй - 1.

2) дискретная биномиальная случайная величина(биномиальное распределение). Закон распределения данной дискретной случайной величины запишется следующим образом: 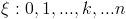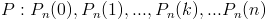где

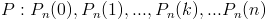
3) дискретная случайная величина Пуассона(пуассоновское распределение с параметром ). Закон распределения дискретной случайной величины Пуассона задается следующим образом: 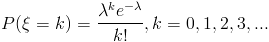где - 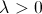параметр.

4) дискретная геометрическая случайная величина (геометрическое распределение). Закон распределения геометрической дискретной случайной величины имеет вид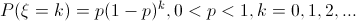

Непрерывные случайные величиныРаспределение случайной величины называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого 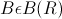, 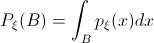где 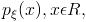- интегрируемая по Лебегу функция. Функция 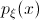называется плотностью распределения случайной величины .

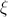Примеры непрерывных случайных величин:

1) нормальная непрерывная случайная величина, или непрерывная случайная величина Гаусса(нормальное распределение). Непрерывная случайная величина 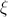имеет нормальное (гауссовское) распределение, если её плотность распределения имеет вид 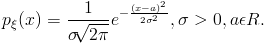Если 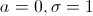, то распределение называется стандартным нормальным распределением.

2)экспоненциальная (показательная) непрерывная случайная величина 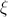(экспоненциальное распределение). Непрерывная случайная величина имеет экспоненциальное(показательное) распределение с параметром 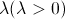, если её плотность имеет вид

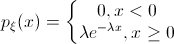3) Равномерная на [a;b] непрерывная случайная величина 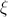(равномерное на отрезке [a;b] распределение).

Равномерно распределенная на отрезке [a;b] непрерывная случайная величина имеет плотность распределения

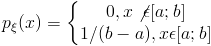Равномерное распределение реализует принцип геометрической вероятности при бросании точки на отрезок [a;b]

22.Законом распределениядискретнойслучайнойвеличиныназываютсоответствиемеждувозможнымизначениямислучайнойвеличины и ихвероятностями Закон распределениядискретнойслучайнойвеличины Х можетбытьзадан в видетаблицы, в первойстрокекоторойуказаны в порядкевозрастания все возможныезначенияслучайнойвеличины, а вовторойстрокесоответствующиевероятностиэтих значений, т.е.

x	x1	x2	х3	…	хn
p	р1	р2	р3	...	рn

где р₁+ р₂+…+ р_n=1

Закон распределениядискретнойслучайнойвеличины Х можноизобразитьграфически, для чего в прямоугольнойсистеме координат строятломаную, соединяющуюпоследовательно точки с координатами (x_i;p_i), i=1,2,…n. Полученнуюлиниюназываютмногоугольникомраспределения (рис.1).

23.