Формулы умножения вероятностей

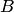Пусть события и независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий и .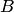

Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

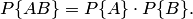
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

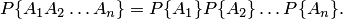
Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие ), 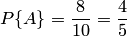. Вероятность того, что из второго ящика взята стандартная деталь (событие 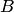), 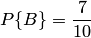. Вероятность того, что из третьего ящика взята стандартная деталь (событие 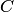), 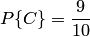. Так как события , 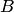и 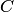независимые в совокупности, то искомая вероятность (по теореме умножения)

Пусть события и 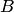зависимые, причем вероятности 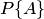и и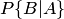звестны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие , и событие .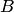

Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие 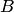) и при третьем — синий (событие ).

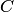Решение. Вероятность появления белого шара при первом испытании 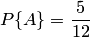. Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность 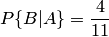. Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный, 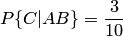. Искомая вероятность

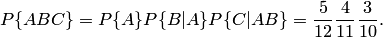
Формула полной вероятности

Теорема 2.5. Если событие наступает только при условии появления одного из событий 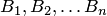, образующих полную группу несовместных событий, то вероятность события равна сумме произведений вероятностей каждого из событий 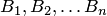на соответствующую условную вероятность события :

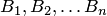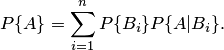
(2.1)

При этом события 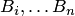называются гипотезами, а вероятности 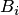— априорными. Эта формула называется формулой полной вероятности.

Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.

Решение. Обозначим событие, означающее годность собранного узла; 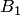, 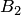и 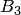— события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда

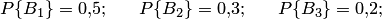
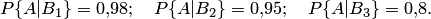
Искомая вероятность

Формула Байеса

Эта формула применяется при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий 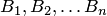, образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез 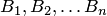. Априорные (до опыта) вероятности 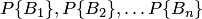известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности 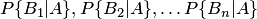. Для гипотезы 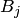формула Байеса выглядит так:

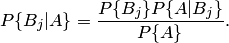
Раскрывая в этом равенстве 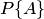по формуле полной вероятности (2.1), получаем

Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.

Решение. Рассчитаем условные вероятности по формуле Байеса:

для первого станка

для второго станка

для третьего станка