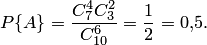Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Произведение событий обозначается

.

Например, если событие есть попадание в цель при первом выстреле, событие 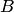— при втором, то событие 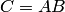состоит в том, что в цель попали при обоих выстрелах.

Понятия суммы и произведения событий имеют наглядную геометрическую интерпретацию. Пусть событие состоит в попадании точки в область 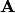, событие 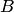— в попадании в область 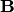, тогда событие 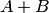состоит в попадании точки в область, заштрихованную на рис. 1, и событие 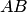— в попадании точки в область, заштрихованную на рис. 2

Классическое определение вероятности случайного события

Для количественного сравнения событий по степени возможности их появления вводится числовая мера, которая называется вероятностью события.

Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.

Вероятность события будем обозначать символом .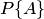

Вероятность события равна отношению числа случаев 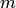, благоприятствующих ему, из общего числа 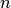единственно возможных, равновозможных и несовместных случаев к числу 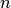, т. е.

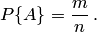
(1.1)

Это есть классическое определение вероятности. Таким образом, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать общее их число 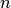, число случаев 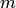, благоприятствующих данному событию, и затем выполнить расчет по формуле (1.1).

Из формулы (1.1) следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев:

.

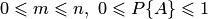Свойства вероятности

Свойство 1. Если все случаи являются благоприятствующими данному событию , то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления 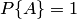, так как в этом случае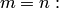

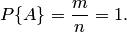
Свойство 2. Если нет ни одного случая, благоприятствующего данному событию , то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления 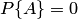, так как в этом случае :

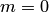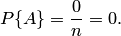
Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.

Свойство 4. Вероятность наступления противоположного события 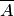определяется так же, как и вероятность наступления, события :

где — число случаев, благоприятствующих появлению противоположного события 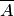. Отсюда вероятность наступления противоположного события 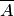равна разнице между единицей и вероятностью наступления события :

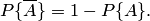
(1.2)

Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.

Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение. Обозначим событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:

.

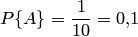Элементы комбинаторики

В теории вероятностей часто используют размещения, перестановки и сочетания. Если дано множество 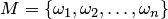, то размещением (сочетанием) из 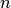элементов по 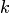называется любое упорядоченное (неупорядоченное) подмножество 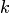элементов множества 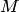. При 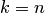размещение называется перестановкой из 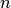элементов.

Пусть, например, дано множество 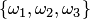. Размещениями из трех элементов этого множества по два являются 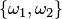, , 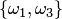, , 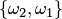, 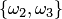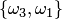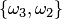; сочетаниями — , , .

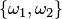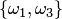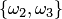Два сочетания различаются хотя бы одним элементом, а размещения различаются либо самими элементами, либо порядком их следования. Число сочетаний из 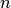элементов по 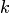вычисляется по формуле

,

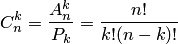где

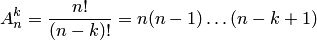
есть число размещений из 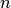элементов по 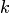; 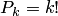— число перестановок из 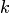элементов.

Пример 2. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди взятых наудачу 6 деталей ровно 4 стандартных.

Решение. Общее число возможных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. равно 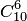— числу сочетаний из 10 элементов по 6. Число исходов, благоприятствующих событию (среди 6 взятых деталей ровно 4 стандартных), определяем так: 4 стандартные детали можно взять из 7 стандартных деталей 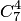способами; при этом остальные 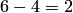детали должны быть нестандартными; взять же 2 нестандартные детали из 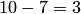нестандартных деталей можно 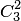способами. Следовательно, число благоприятствующих исходов равно 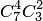. Исходная вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов: