Методы расчета электрических цепей.
Методическая разработка
по дисциплине «Электротехника»
«Расчет электрических цепей»
Часть 1
МР.В43.02-09
МР.Т39.02-09
Автор_____Д.А.Коренева

Дата
| РАССМОТРЕНО на заседании ЦК _______________ наименование ЦК Председатель___________________ Протокол заседания ЦК от________200_ №____ | УТВЕРЖДАЮ Зам. директора по УР _________И.Е. Игольникова |
РЕКОМЕНДОВАНО
Методическим советом
Протокол заседания
от________200_ №____
Зам. директора по УМНР
____________О.Б. Кузнецова
Аннотация
(Краткое описание работы)
Автор: Д.А. Коренева
Рецензенты Методист ФГОУСПО ЧЭМК Лисицына И.В. ___________
Доцент кафедры ТОЭ
ЧГУ им. И.Н. Ульянова
Нестерина А.Д. __________
Содержание
Введение………………………………………………….....4
1. Методы расчета электрических цепей………………….5
1.1 Метод суперпозиций…………………………………...5
1.2 Метод узловых и контурных уравнений……………..13
1.3 Метод узловых потенциалов………………………….16
1.4 Метод контурных токов……………………………….21
1.5 Метод эквивалентного генератора…………………...24
2.Расчетно-графическая работа №1
«Электрические цепи постоянного тока»………………..29
2.1 Задание…………………………………………………29
Приложение 1. Схемы для расчета по вариантам………31
Приложение 2. Задание для студентов по вариантам…..45
Введение
Дисциплина «Электротехника» для специальностей 140603, 140613 и 230101 является основополагающим предметом, на знании основных законов и навыков которого базируется изучение специальных дисциплин «Электрические аппараты», «Электрические машины» и т.д.
Поэтому изучение предмета должно быть углублено путем увеличения самостоятельной индивидуальной работы студентов.
Для этого преподавателем разработаны индивидуальные задания, позволяющие преподавателю легко контролировать уровень усвоения материала, глубину понимания отдельных схем.
При изучении темы «Расчет электрических цепей постоянного тока» студент должен знать: 1-ый, 2-ой законы Кирхгофа, закон Ома, что такое узел, ветвь, контур; определять их количество в схеме.
Студент должен уметь:
- рассчитывать токи в разветвленной электрической цепи методом суперпозиций;
- рассчитывать ток одной из ветвей методом эквивалентного генератора;
- составлять систему уравнений:
по первому и второму законам Кирхгофа;
для нахождения контурных токов;
для нахождения узловых потенциалов;
и решать их одним из способов, изученных в курсе математики.
Данная методическая разработка позволяет студенту самостоятельно провести расчет электрической схемы и произвести проверку результата балансом мощности.
Методы расчета электрических цепей.
Метод суперпозиций
Метод используется только для расчета линейных электрических цепей.
  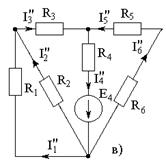 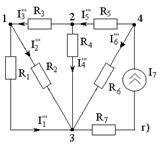 | Методика расчета: 1) Произвольно задаются направления токов в ветвях. 2) На основе исходной схемы составляются частные расчетные схемы, в каждой из которых действует только один источник. 3) Любым методом определяют токи в частных схемах (б, в, г). б) 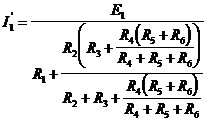 , , 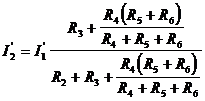 ; ; 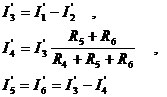 в) в) 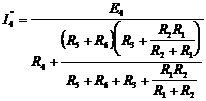 , , 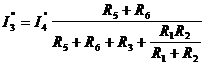 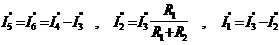 г) г) 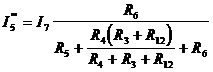 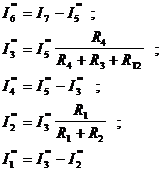 |
4) Ток в ветви исходной схемы (а) равен алгебраической сумме частных токов ветви.
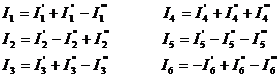
Вывод: если в результате расчета какие-либо токи получатся отрицательными, значит направление токов выбрано неверно.
Проверка правильности расчета — баланс мощности.
Примечание: при исключении источники Е закорачиваются, источники I разрываются.
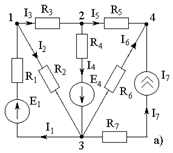
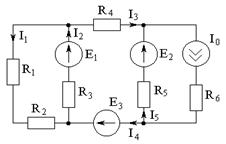
Пример расчета:
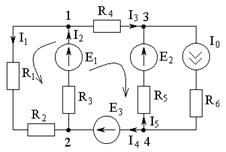 | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: все токи. |
Решение:
1. Зададим направления токов в ветвях схемы:
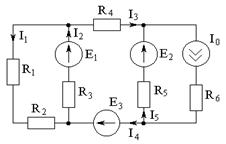
2. На основе исходной схемы составляем частные расчетные схемы. В схеме 4 источника – составляем 4 частные расчетные схемы.
а) Оставляем источник Е1, а Е2, Е3 закорачиваем (пустой провод), источник I0 разрываем (ветвь не рисуем):
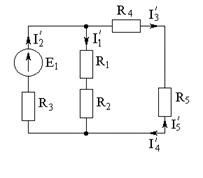
Сопротивления R4 и R5 соединены последовательно; R1 и R2 – последовательно, тогда после преобразования:
R4,5=R4+R5=25Ом R1,2=R1+R2=25 Ом
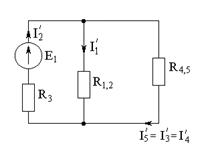
Сопротивления R1,2 и R4,5 соединены параллельно, тогда:
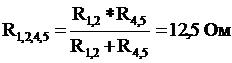
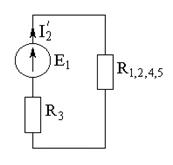 Сопротивления R3 и R1,2,4,5 соединены последовательно с источником Е1, тогда:
Сопротивления R3 и R1,2,4,5 соединены последовательно с источником Е1, тогда:
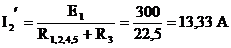
Токи 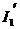 и
и 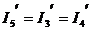 в параллельных ветвях можно рассчитать по формуле «чужого сопротивления», а так как сопротивления этих ветвей одинаковы, тогда:
в параллельных ветвях можно рассчитать по формуле «чужого сопротивления», а так как сопротивления этих ветвей одинаковы, тогда:
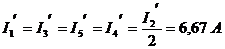
б) Оставляем источник E2, а источники: E1, E3 закорачиваем, I0 – разрываем.
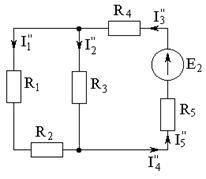
Расчет схемы можно провести аналогично пункту а), а можно и короче:
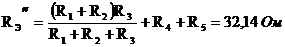
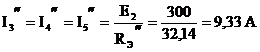
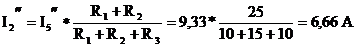
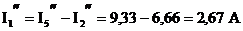
в) Оставляем источник E3, источники: E1, E2 - закорачиваем, I0 – разрываем.
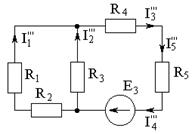
Аналогично пункту б):
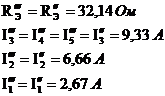
г) Оставляем источник I0, а Е1, E2, E3 – закорачиваем:
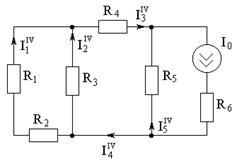
Резисторы R1 и R2 соединены последовательно, а резисторы R1,2 и R5 – параллельно:
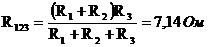
R4 и R1,2,3 – последовательно;
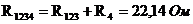 .
.
Тогда по формуле чужого сопротивления:
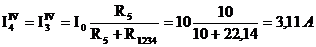
По первому закону Кирхгофа:
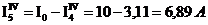
По формуле «чужого сопротивления»:
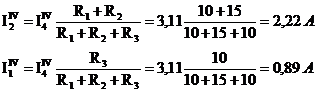
3. Токи в ветвях исходной схемы определяем по формулам:
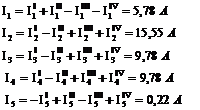
Частные токи 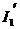 и
и 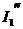 в первой формуле со знаком «+», так как они совпадают по направлению с исходным током I1, а
в первой формуле со знаком «+», так как они совпадают по направлению с исходным током I1, а 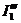 и
и 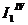 со знаком «-», так как они не совпадают по направлению с
со знаком «-», так как они не совпадают по направлению с 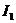 ! Токи остальных ветвей – аналогично.
! Токи остальных ветвей – аналогично.
Все токи получились положительными, значит их направление выбрано верно.
Метод узловых потенциалов
Метод позволяет сократить число уравнений в системе до n–1 (n—количество узлов).
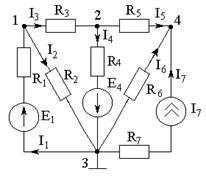 | Узловым напряжением называется разность потенциалов между данным узлом и базисным (jк-го=0). По I-му закону Кирхгофа для независимых узлов (1,2,4): 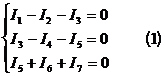 |
По обобщенному закону Ома токи в ветвях:

Для “1” узла: 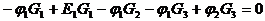
Перепишем систему уравнений (1):
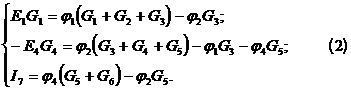
Методика расчета:
1) Произвольно задаются направления I-ов в ветвях.
2) Намечается базисный узел (j=0) и все независимые узлы.
3) Составляется система уравнений для независимых узлов типа :
в левой части уравнения — S произведений Е ветвей, сходящихся в данном узле, на соответствующие им проводимости и S источников тока;
в правой части уравнения — произведение j рассматриваемого узла и суммы проводимостей ветвей, сходящихся в данном узле, минус j противоположных концов этих ветвей, умноженных на проводимости этих ветвей.
4) ЭДС (I0) учитывается со знаком “+”, если направлена в данный узел, и наоборот.
5) Решаем систему уравнений любым известным из математики способом.
6) Определяем токи в ветвях по обобщенному закону Ома.
Вывод : Если в результате расчета какие-либо токи получатся отрицательными, значит направление токов выбрано неверно.
Проверка правильности расчета — баланс мощности.
Примечание — если в схеме есть ветвь с чистой Е (без R), то в качестве нулевого j необходимо взять один из узлов данной ветви, а ток ветви рассчитывается по I-му закону Кирхгофа.
Частный случай: Метод 2-х узлов.
Можно применять в схемах, имеющих любое количество активных или пассивных ветвей, но только два узла.
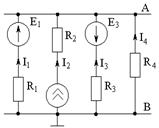 | Методика расчета : 1) Направление токов в ветвях задается произвольно, но к одному узлу. 2) Записывается уравнение узлового U, причем ЭДС считается “+”, если направление I и Е ветви совпадают, и наоборот : 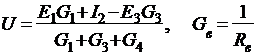 |
3) Определяются токи ветвей по формуле:
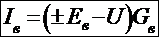
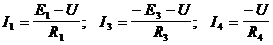
Е считается “+”, если направлениеЕ и I ветви совпадают.
Вывод и проверка — см. Выше.
1) ЕслиЕ ветви> U, то источник работает в режиме генератора.
2) Если Е ветви< U, то источник работает в режиме потребителя.
3) Если Е ветви = U, то источник работает в режиме Х.Х. и её можно включить и отключить не нарушая рабочего режима работы.
4) Если в ветви только чистая Е, то U=Ев и нет необходимости рассчитывать U между узлами.
Пример решения:
 | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: все токи. |
Решение:
1. Задаем направления токов в ветвях.
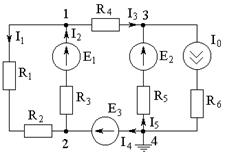
2. Задаем базисный узел (φ4=0), так как он принадлежит к ветке с чистой Е3 (без резистора), остальные узлы соответственно с потенциалами φ1, φ2, φ3.
Тогда φ1=Е3=300 В.
3. Составляем систему уравнений для независимых узлов (2,3):
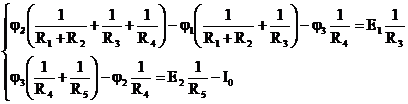
Решим систему методом подстановки:
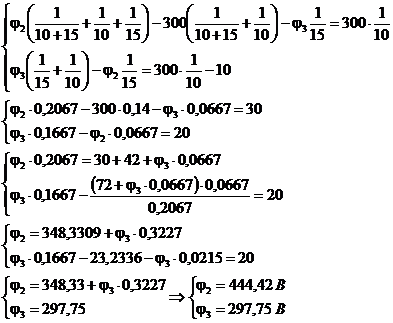
4. По обобщенному закону Ома находим токи в ветвях схемы. Ток ветви прямо пропорционален разности потенциалов концов ветви, по которой протекает ток (ток течет от большего потенциала к меньшему) и ЭДС ветви («+» - если ЭДС совпадает по направлению с током) и обратно пропорционален сопротивлению ветви.
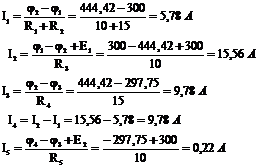
В результате расчета все токи получились положительные, значит их направление выбрано верно. Значения токов совпали со значениями предыдущих токов.
Решение верно.
Метод контурных токов
Метод позволяет уменьшить число уравнений до (m-n+1).
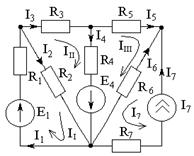 | Методика расчета: 1) Произвольно задаются направления токов в ветвях. 2) Произвольно задаются направления контурных токов в независимых контурах схемы. Контурный ток — расчетная величина, которая одинакова для всех ветвей данного контура. Контурный ток равен действительному току ветви, которая принадлежит только данному контуру. |
3) Составляются уравнения для определения действительных токов:
для смежных ветвей — наложением контурных токов, соответствующих смежных контуров;
для независимых ветвей — если контурный ток совпадает с направлением I ветви, то Iв=Iк, если не совпадает, то Iв= –Iк.
I1=II; I3=III; I5=IIII — для независимых ветвей;
I2=II–III; I4=III–IIII; I6=–IIII–I7 — для ветвей смежных контуров.
4) По II-му закону Кирхгофа составляются контурные уравнения:
ЭДС считается положительной, если направления ЭДС и контурного тока совпадают и наоборот;
падение напряжения от собственного контурного тока всегда “+”;
падение напряжения от смежного контура в ветви их соприкосновения будет “+”, если направления контурных токов в ветви соприкосновения смежных контуров совпадают и наоборот.
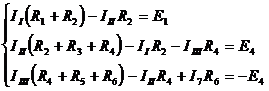
5) Полученная система решается любым известным из математики способом, и определяются величины контурных токов.
6) По уравнениям п.3 определяются реальные токи.
Вывод: Если в результате расчета какие-либо токи получатся отрицательными, значит направление токов выбрано неверно.
Проверка правильности расчета — баланс мощности.
Примечание: Для контура, содержащего источник тока, уравнение по II-му закону Кирхгофа не записывается, но падение напряжения в смежном контуре от данного контура учитывается на общих основаниях (см. уравнение 3 п.4)
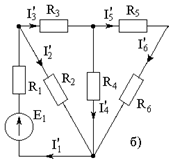
Пример решения:
 | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: все токи. |
Решение:
1. Задаем направления токов в ветвях.
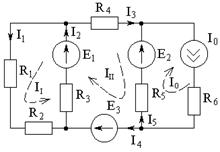
2. Задаем направление контурных токов в независимых контурах схемы (II, III, I0).
3. По второму закону Кирхгофа составляем контурные уравнения для контуров с токами II и III.
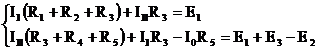
Для контура I0 уравнение не составляется, так как он содержит источник тока.
Решим систему методом подстановки.
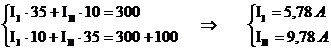
4. Определяем действительные токи ветвей.
- для независимых ветвей:
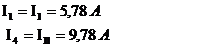
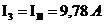
- для ветвей смежных контуров:
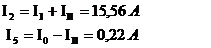
В результате расчета все токи получились положительные, значит их направление выбрано верно. Значения токов совпали со значениями предыдущих токов.
Решение верно.
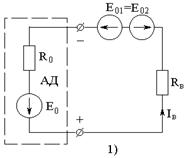
Вывод формулы
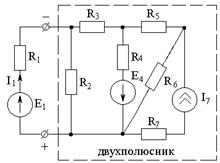 | 1) При анализе цепи используем метод наложения: в выделенную ветвь включаем 2 источника ЭДС, равные по величине, но противоположные по направлению. При этом ток в схеме не изменится. |
|
2) Исключаем поочередно действия источников Е01 и Е02. При Е01=0, I=0, если внутреннюю ЭДС двухполюсника компенсирует действие ЭДС Е02=Е0.
3) Е01 является внутренней ЭДС двухполюсника. Ток ветви и ЭДС сонаправлены.
R0 — внутреннее сопротивление двухполюсника относительно зажимов исследуемой ветви.
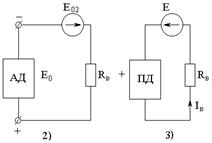
Определение E0 и R0
| Схема | Опыт | Расчет |
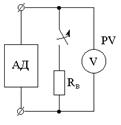 | 1) Опыт ХХ 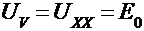 | Размыкается исследуемая ветвь и любым из известных методов рассчитывается разность потенциалов на разомкнутых зажимах, причем больший потенциал определяется по направлению тока в исследуемой ветви. |
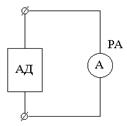 | 2) Опыт КЗ Вместо Rв ставится РА 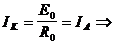 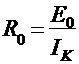 | Все источники Е внутри двухполюсника закорачиваются (тока — разрываются) и определяется эквивалентное R относительно зажимов выделенной ветви. |
4) Ток ветви определяется по формуле:
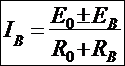
Пример решения:
 | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: I2. |
Решение:
В ветви с током I2 содержится ЭДС Е2, направленное по току, и резистор R3. По основной расчетной формуле:
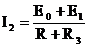
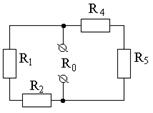
а) Определим сопротивление эквивалентного генератора R0.
Резисторы R1 и R5 соединены последовательно, R4 и R5 - последовательно, а R1,2 и R4,5 – параллельно, следовательно:
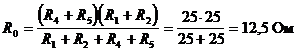
б) Определим ЭДС эквивалентного генератора Е0.
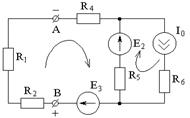
Ток I2 в исходной схеме направлен от клеммы В к клемме А, тогда:
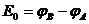 , или
, или
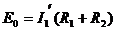
По методу контурных токов
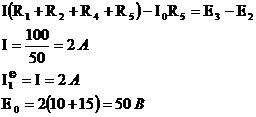
Ток во второй ветви:
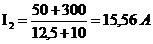
В результате расчета ток I2 получился положительным и совпал по величине с предыдущими расчетами.
Решение верно
Задание.
1. Определить токи во всех ветвях схемы методом:
а) «узловых и контурных уравнений»;
б) «контурных токов»;
в) «узловых потенциалов»;
г) «наложения (суперпозиций)».
2. Составить баланс мощностей. Проверить правильность расчетов.
3. Определить методом «эквивалентного генератора» обозначенный в схеме ток.
4. Определить показание вольтметра, включенного между точками А и В.
Приложение 1. Схемы по расчетам по вариантам
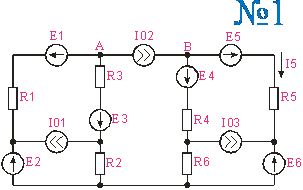
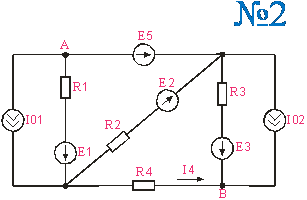
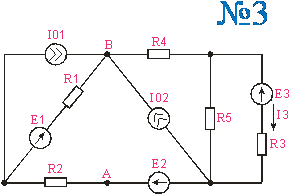
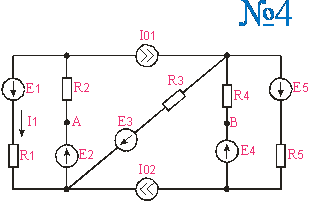
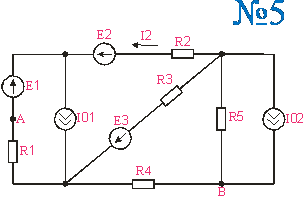
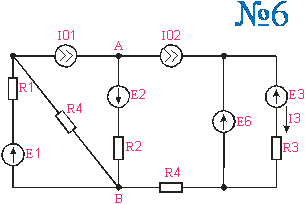
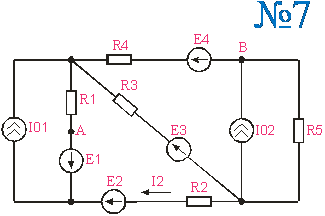
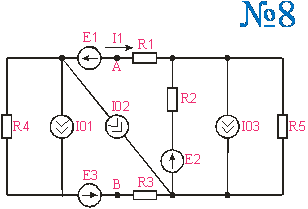
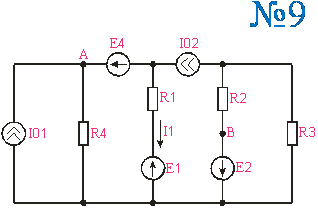
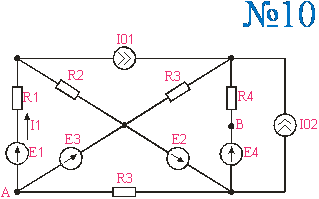
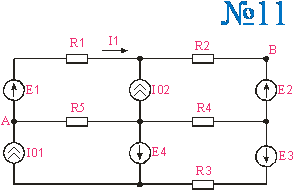
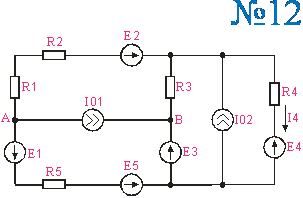
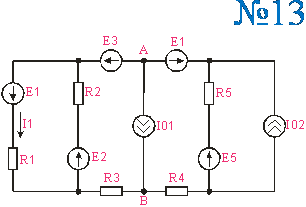
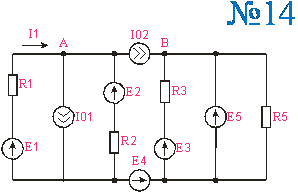
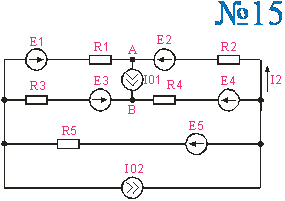
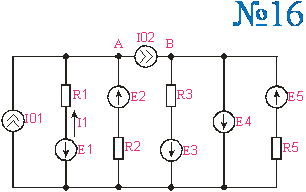
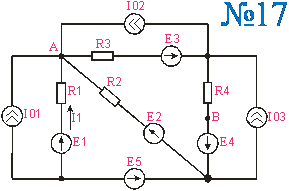
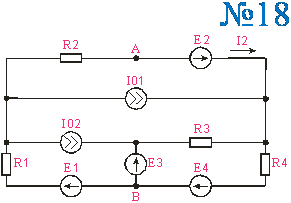
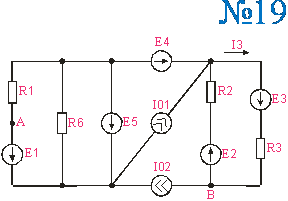
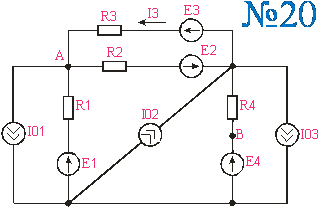
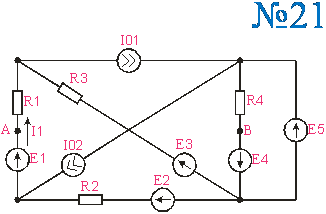
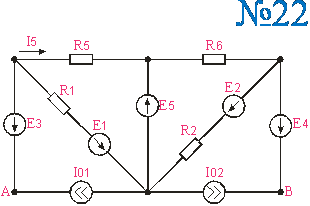
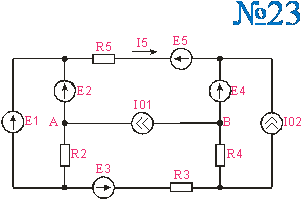
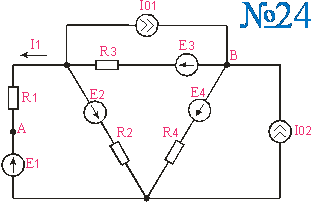
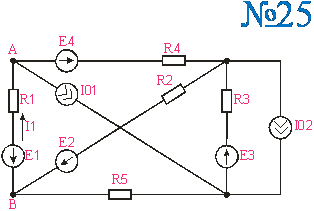
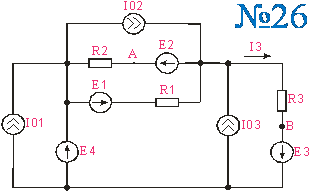
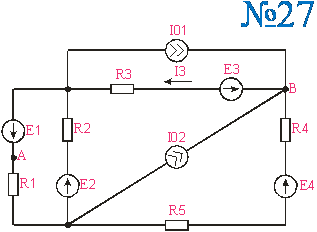
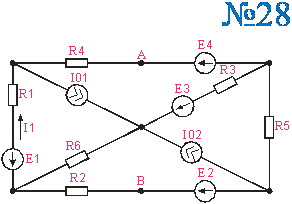
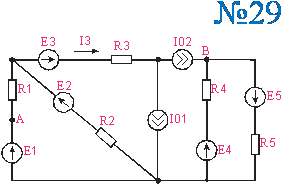
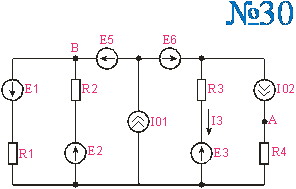
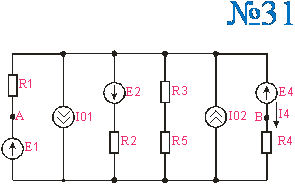
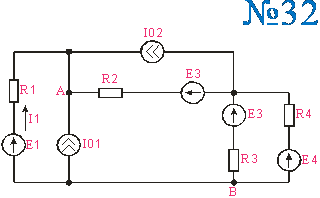
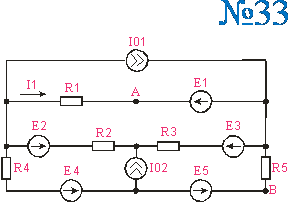
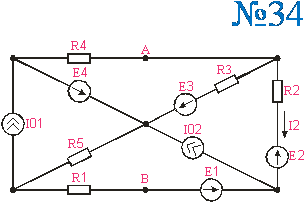
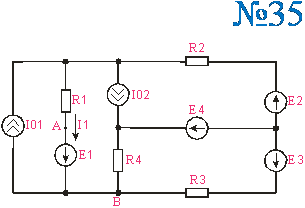
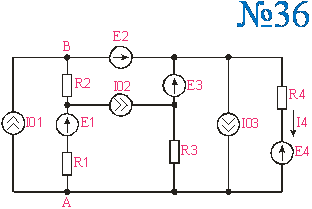
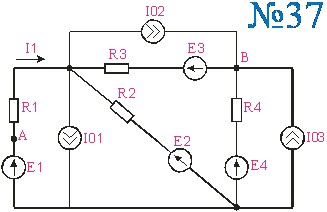
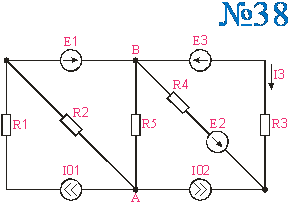
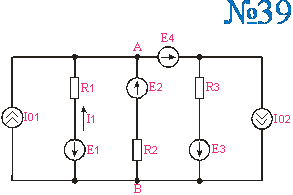
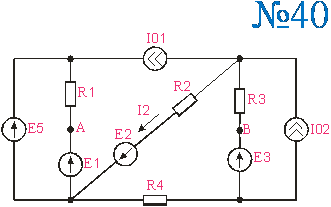
Приложение 2.
Задание для студентов по вариантам.
| № | Е1=Е4 | Е2=Е5 | Е3=Е6 | R1=R4 | R2=R5 | R3=R6 | I01=I02=I03 |
| В | В | В | Ом | Ом | Ом | А | |
| 1…10 | |||||||
| 11…20 | |||||||
| 21…30 | |||||||
| 31…40 |
Методическая разработка
по дисциплине «Электротехника»
«Расчет электрических цепей»
Часть 1
МР.В43.02-09
МР.Т39.02-09
Автор_____Д.А.Коренева

Дата
| РАССМОТРЕНО на заседании ЦК _______________ наименование ЦК Председатель___________________ Протокол заседания ЦК от________200_ №____ | УТВЕРЖДАЮ Зам. директора по УР _________И.Е. Игольникова |
РЕКОМЕНДОВАНО
Методическим советом
Протокол заседания
от________200_ №____
Зам. директора по УМНР
____________О.Б. Кузнецова
Аннотация
(Краткое описание работы)
Автор: Д.А. Коренева
Рецензенты Методист ФГОУСПО ЧЭМК Лисицына И.В. ___________
Доцент кафедры ТОЭ
ЧГУ им. И.Н. Ульянова
Нестерина А.Д. __________
Содержание
Введение………………………………………………….....4
1. Методы расчета электрических цепей………………….5
1.1 Метод суперпозиций…………………………………...5
1.2 Метод узловых и контурных уравнений……………..13
1.3 Метод узловых потенциалов………………………….16
1.4 Метод контурных токов……………………………….21
1.5 Метод эквивалентного генератора…………………...24
2.Расчетно-графическая работа №1
«Электрические цепи постоянного тока»………………..29
2.1 Задание…………………………………………………29
Приложение 1. Схемы для расчета по вариантам………31
Приложение 2. Задание для студентов по вариантам…..45
Введение
Дисциплина «Электротехника» для специальностей 140603, 140613 и 230101 является основополагающим предметом, на знании основных законов и навыков которого базируется изучение специальных дисциплин «Электрические аппараты», «Электрические машины» и т.д.
Поэтому изучение предмета должно быть углублено путем увеличения самостоятельной индивидуальной работы студентов.
Для этого преподавателем разработаны индивидуальные задания, позволяющие преподавателю легко контролировать уровень усвоения материала, глубину понимания отдельных схем.
При изучении темы «Расчет электрических цепей постоянного тока» студент должен знать: 1-ый, 2-ой законы Кирхгофа, закон Ома, что такое узел, ветвь, контур; определять их количество в схеме.
Студент должен уметь:
- рассчитывать токи в разветвленной электрической цепи методом суперпозиций;
- рассчитывать ток одной из ветвей методом эквивалентного генератора;
- составлять систему уравнений:
по первому и второму законам Кирхгофа;
для нахождения контурных токов;
для нахождения узловых потенциалов;
и решать их одним из способов, изученных в курсе математики.
Данная методическая разработка позволяет студенту самостоятельно провести расчет электрической схемы и произвести проверку результата балансом мощности.
Методы расчета электрических цепей.
Метод суперпозиций
Метод используется только для расчета линейных электрических цепей.
    | Методика расчета: 1) Произвольно задаются направления токов в ветвях. 2) На основе исходной схемы составляются частные расчетные схемы, в каждой из которых действует только один источник. 3) Любым методом определяют токи в частных схемах (б, в, г). б) 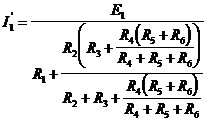 , , 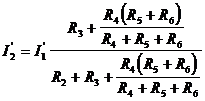 ; ; 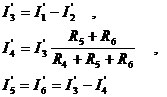 в) в) 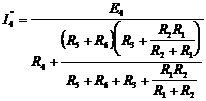 , , 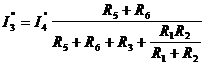 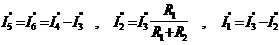 г) г) 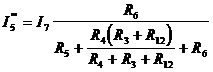 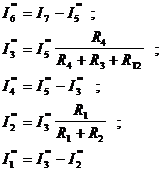 |
4) Ток в ветви исходной схемы (а) равен алгебраической сумме частных токов ветви.
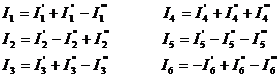
Вывод: если в результате расчета какие-либо токи получатся отрицательными, значит направление токов выбрано неверно.
Проверка правильности расчета — баланс мощности.
Примечание: при исключении источники Е закорачиваются, источники I разрываются.
Пример расчета:
 | Дано: Е1=Е2=Е3=300 В R1=R3=R5=R6=10 Ом R2=R4=15 Ом I0=10 A Найти: все токи. |
Решение:
1. Зададим направления токов в ветвях схемы:

2. На основе исходной схемы составляем частные расчетные схемы. В схеме 4 источника – составляем 4 частные расчетные схемы.
а) Оставляем источник Е1, а Е2, Е3 закорачиваем (пустой провод), источник I0 разрываем (ветвь не рисуем):

Сопротивления R4 и R5 соединены последовательно; R1 и R2 – последовательно, тогда после преобразования:

R4,5=R4+R5=25Ом R1,2=R1+R2=25 Ом
Сопротивления R1,2 и R4,5 соединены параллельно, тогда:
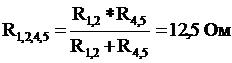
 Сопротивления R3 и R1,2,4,5 соединены последовательно с источником Е1, тогда:
Сопротивления R3 и R1,2,4,5 соединены последовательно с источником Е1, тогда:
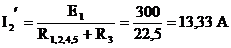
Токи 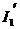 и
и 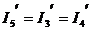 в параллельных ветвях можно рассчитать по формуле «чужого сопротивления», а так как сопротивления этих ветвей одинаковы, тогда:
в параллельных ветвях можно рассчитать по формуле «чужого сопротивления», а так как сопротивления этих ветвей одинаковы, тогда:
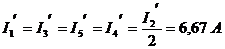
б) Оставляем источник E2, а источники: E1, E3 закорачиваем, I0 – разрываем.

Расчет схемы можно провести аналогично пункту а), а можно и короче:
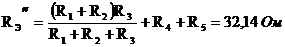
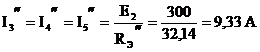
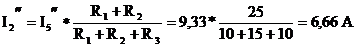
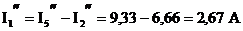
в) Оставляем источник E3, источники: E1, E2 - закорачиваем, I0 – разрываем.

Аналогично пункту б):
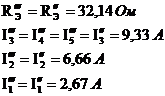
г) Оставляем источник I0, а Е1, E2, E3 – закорачиваем:

Резисторы R1 и R2 соединены последовательно, а резисторы R1,2 и R5 – параллельно:
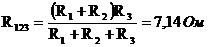
R4 и R1,2,3 – последовательно;
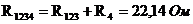 .
.
Тогда по формуле чужого сопротивления:
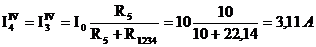
По первому закону Кирхгофа:
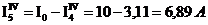
По формуле «чужого сопротивления»:
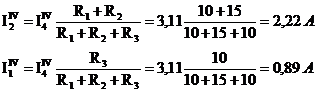
3. Токи в ветвях исходной схемы определяем по формулам:

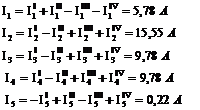
Частные токи 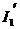 и
и 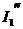 в первой формуле со знаком «+», так как они совпадают по направлению с исходным током I1, а
в первой формуле со знаком «+», так как они совпадают по направлению с исходным током I1, а 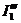 и
и 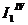 со знаком «-», так как они не совпадают по направлению с
со знаком «-», так как они не совпадают по направлению с 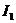 ! Токи остальных ветвей – аналогично.
! Токи остальных ветвей – аналогично.
Все токи получились положительными, значит их направление выбрано верно.