Тема 1. Определение вероятности

Тема 1. Определение вероятности

№1. Игральная кость бросается один раз. Тогда вероятность того, что число очков, выпавших на верхней грани, будет меньше трех, равна …

Тема 2. Теоремы сложения и умножения вероятностей

№2.1 Из урны, содержащей 6 белых и 4 черных шара извлекают без возвращения 2 шара. Определить вероятность того, что первым извлекли белый, а вторым черный

2.2 Из урны, содержащей 7 белых и 3 черных шара извлекают без возвращения 2 шара. Определить вероятность того, что хотя бы один из извлеченных белый.

2.3 В электрической сети последовательно включены 2 элемента, работающие независимо друг от друга. Вероятности отказа элементов 0,2 и 0,15. Тогда вероятность того, что ток в цепи будет равна.

2.4 В партии из 10 деталей имеется 3 бракованные. Наудачу отобраны три детали. Тогда вероятность того, что все отобранные детали будут бракованными, равна …

2.5 Студент сдает 2 экзамена. Пусть А- студент сдал первый экзамен, В – студент сдал второй экзамен. Тогда событие С - студент сдал только один экзамен, записывается в виде

Тема 3 Полная вероятность. Формула Байеса.

3.1 В первой урне 3 черных и 7 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …

3.3 При сборке изделий используются детали с двух предприятий. С первого поступает 30%, со второго 70%. Вероятность того, что деталь первого предприятия исправна 0,8; второго 0,7. определить вероятность того, что случайно взятое изделие неисправно

3.4 Событие А может наступить лишь при условии появления одного из двух несовместных событи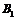й и 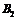, образующих полную группу событий. Известны вероятность 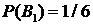и условные вероятности 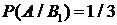, 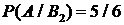. Тогда вероятность 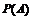равна…

3.5 Несовместные события А, В, С не образуют полную группу событий, если их вероятности равны…

1	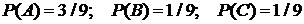2.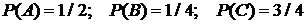
3.	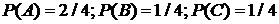4.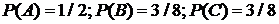

Тема №4. Законы распределения вероятностей дискретных случайных величин

4.1 Дискретная случайная величина 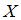задана законом распределения вероятностей:

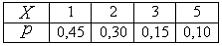
Тогда вероятность 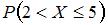равна …

4.4 Дискретная случайная величина 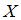задана законом распределения вероятностей:

	0,1	0,25	a	0,3

4.5 Задан закон распределения дискретной случайной величины.

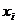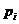	0,7	0,3

Найти ее функцию распределения

4.4 Дискретная случайная величина 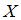задана законом распределения вероятностей:

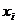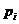	a	0,2	b	c

Тогда a, b, c могут быть равны

А) a=0,3, b=0,5, c=0,2 В) a=0,1, b=0,2, c=0,3

А) a=0,3, b=0,4, c=0,1 В) a=0,2, b=0,2, c=0,2

Тема №5. Законы распределения вероятностей непрерывных случайных величин

5.2 Плотность распределения случайной величины имеет вид: 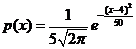. Тогда ее математическое ожидание и среднее квадратическое отклонение равно

Функция распределения равномерно распределенной случайной величины изображена на рисунке. Тогда ее дисперсия равна

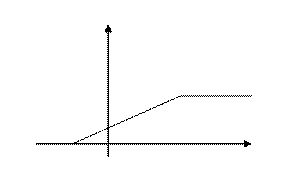
Тема №6. Числовые характеристики дискретных случайных величин

6 Задан закон распределения дискретной случайной величины. Найти ее М(х) и Д(х)

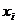	-1
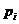	0,7	0,2	0,1

Тема 1. Определение вероятности

№1. Игральная кость бросается один раз. Тогда вероятность того, что число очков, выпавших на верхней грани, будет меньше трех, равна …