Тема 40. Элементы теории игр

Тема 40. Элементы теории игр

Игровые модели и их классификация

Определение 1. Конфликтной ситуацией (конфликтом)называют явление или ситуацию, в которой участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия.

Определение 2. Упрощенную формализованную модель конфликтной ситуации называют игрой.

Замечание. От реального конфликта игра отличается наличием правил игры.

Теория игр – раздел прикладной математики, занимающийся построением математических моделей возможных конфликтных ситуаций и разработкой методов решения возникающих в этих ситуациях задач.

Определение 3. Заинтересованные стороны конфликта называют игроками.

Определение 4. Каждое действие игрока в рамках правил игры и в зависимости от ситуации, сложившейся в процессе игры, называют ходом или стратегией игрока.

Определение 5. Число, выражающее степень удовлетворения интересов игрока в данной ситуации, называют выигрышем игрока.

Определение 6. Зависимость величины выигрыша игрока от всевозможных стратегий называют функцией выигрыша (платежной функцией).

Определение 7. Значение функции выигрыша называют исходом игры.

Замечание. В теории игр предполагают, что функции выигрыша и множество доступных для каждого игрока стратегий известны, то есть каждый игрок знает как свои функции выигрыша и набор имеющихся в его распоряжении стратегий, так и функции выигрыша и стратегии остальных игроков. В соответствии с этой информацией он и организует свое поведение, то есть определяет выбор своей стратегии. Суть игры заключается в том, что каждый из игроков принимает такие решения, которые, как он полагает, могут обеспечить ему наилучший результат (исход).

Определение 8. Стратегию называют оптимальной, если она при многократном повторении обеспечивает данному игроку максимально возможный средний выигрыш.

Основные направления изучения теории игр

1) выработка принципов оптимальности – критериев, по которым поведение игроков следует считать оптимальным;

2) выяснение реализуемости принципов оптимальности – установление оптимальных в выработанном смысле ситуаций, отыскание их реализаций.

Определение 9. Игровую ситуацию называют равновесной (равновесием), если в ее нарушении не заинтересован ни один из игроков.

Замечание.Равновесие является одной из форм представления об оптимальности в игре, так как в равновесной ситуации каждый игрок получает наибольший выигрыш.

Определение 10.Если в игре существуют стратегии, приводящие к равновесной ситуации, то такие стратегии называют чистыми.

Определение 11. Если в игре не существует стратегий, приводящих к равновесной ситуации, но существуют комбинации исходных стратегий, приводящие к равновесию, то такие комбинации называют смешанными стратегиями.

Замечание.Часто смешанную стратегию представляют как случайный выбор игроками чистых стратегий, при котором случайные выборы различных игроков независимы в совокупности, а выигрыш каждого из них определяется как математическое ожидание случайного выигрыша.

Определение 12. Игру, в которой не существует равновесия, достигаемого чистыми стратегиями, но достигаемого смешанными стратегиями, называют смешанным расширением исходной игры.

Классификация игр

№ п/п	Признак	Класс игр
1.	Число игроков	Парные игры (два игрока)
Множественные игры (три и более игроков)
Игры с бесконечным числом игроков
2.	Количество стратегий	Конечные игры (конечное число стратегий у каждого игрока)
Бесконечные игры (бесконечное число стратегий у каждого игрока)
3.	Свойства функции выигрыша	Игры с нулевой суммой или антагонистические игры (выигрыш одного игрока равен проигрышу другого)
Игры с постоянной разностью (игроки выигрывают и проигрывают одновременно и им выгодно согласовывать свои действия)
Игры с ненулевой суммой (возможны и конфликты и согласованные действия)
4.	Возможность ведения переговоров	Кооперативные (коалиционные) игры (игроки могут договариваться о совместных стратегиях)
Некооперативные игры (игроки не имеют возможности договариваться)
5.	Характер действий игроков	Позиционные игры (игроки совершают действия последовательно, друг за другом)
Непозиционные игры (игроки действуют одновременно)

Матричные игры

Определение 13. Игру, в которой участвуют два игрока, называют парной игрой.

Пусть в игре участвуют два игрока А и В. Каждый из игроков располагает конечным числом чистых стратегий. Обозначим их соответственно: 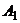, , 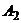…, 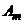– стратегии первого игрока, 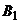, , 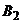…, 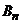– стратегии второго игрока. Игрок А может выбрать любую чистую стратегию 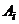, , 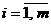в ответ на которую игрок В может выбрать любую свою чистую стратегию 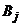, 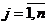. Если игра состоит только из личных ходов, то выбор пары стратегий 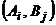однозначно определяет результат 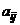– выигрыш игрока А. При этом проигрыш игрока В составит 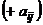(выигрыш игрока В равен 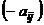). Если известны значения 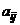для каждой пары 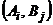чистых стратегий, то можно составить матрицу выигрышей игрока А (проигрышей игрока В) .

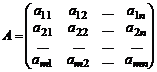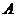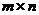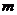Определение 14. Прямоугольную матрицу размерности , где (число строк) – число чистых стратегий первого игрока, а 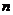(число столбцов) – число стратегий второго игрока, а в клетках указаны выигрыши игроков для каждой ситуации, называют платежной матрицей игры (матрицей выигрышей, матрицей платежей) первого игрока.

Определение 15. Игры двух игроков, функции выигрышей которых можно представить в виде матриц, называют матричными.

Замечание 1. Платежная матрица второго игрока: .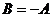

Замечание 2.Для наглядности матрицы выигрышей обоих игроков объединяют в биматрицу игры, элементами которой являются упорядоченные пары, состоящие из выигрыша первого и проигрыша второго игрока при данной стратегии:

.

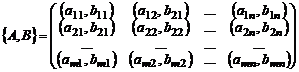Пример 40.1. Два игрока независимо друг от друга записывают любое целое число. Если выписанные числа имеют одинаковую четность, то игрок А получает от игрока В один рубль, а если разную, то наоборот, игрок А платит игроку В один рубль. Требуется составить платежную матрицу игры.

Решение. Игрок А имеет две стратегии: 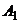– записать четное число, 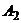– записать нечетное число. Игрок В также имеет две стратегии: 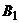– записать четное число, 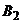– записать нечетное число. Выбор игроками соответствующих стратеги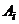й и 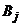однозначно определяет исход игры: 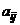– выигрыш игрока А. Стратегиям 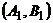и 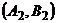соответствует выигрыш игрока А, равный одному рублю, а стратегиям 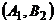и 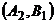соответствует проигрыш игрока, равный одному рублю. Тогда платежные матрицы игроков и биматрица игры будут иметь вид

, , .

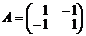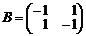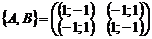Пример 40.2.Две фирмы функционируют на рынке одновременно с одинаковым товарным объемом 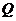. У обеих фирм по соображениям рентабельности есть следующие стратегии: либо вбросить на рынок полный объем товара 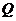, либо выбросить на рынок половину объема 0,5 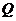. Если первая фирма выбрасывает на рынок полный объем товара, а вторая – половину объема, то первая фирма получает 100 % запланированной прибыли, а вторая – только 25 %, и наоборот. Если обе фирмы выбрасывают на рынок по полному объему прибыли, то получат по 15 % прибыли; если по половине объема, то прибыль каждой из фирм составит по 50 % от запланированной.

Решение. Обозначим 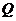– объем товара для каждой из фирм. Для первой фирмы возможны две стратегии: 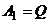, 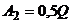(выбросить на рынок весь объем товара или его половину). Аналогично для второй фирмы: 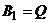, 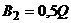(выбросить на рынок весь объем товара или его половину). Примем долю прибыли (в процентах от запланированной) за значение выигрыша при каждой стратегии. Тогда возможны следующие ситуаци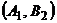и: и 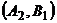– одна из фирм выбросила 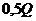товара, а другая 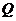товара; 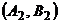– обе фирмы выбросили по 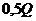товара. Запишем матрицы выигрышей обеих фирм и биматрицу игры:

, , .

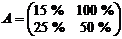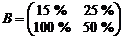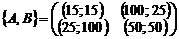Пример 40.3. Две конкурирующие фирмы борются за рынки сбыта, других конкурентов в этом сегменте нет (дуополия). В этом случае каждый из игроков может назвать цену p, по которой он хочет продать определенное количество товара. При этом полагается, что потребители приобретут товар у фирмы, объявившей меньшую цену. В случае объявления одинаковой цены спрос 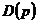распределяется между фирмами поровну.

Решение. Каждый из игроков обладает бесконечным числом стратегий. Функция выигрышей игроков характеризует величины дохода фирм в зависимости от объявленных цен. Так как доход фирмы 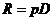, то функцию выигрышей игроков можно представить в виде

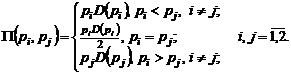
Упрощение платежных матриц

Поиск оптимальных стратегий тем сложнее, чем больше размерность платежной матрицы. Поэтому поиск оптимальных стратегий начинают с упрощения платежной матрицы.

Определение 32. Если в платежной матрице элементы 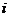-ой строки не меньше соответствующих элементов 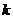-ой строки, то есть 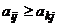( 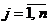), то стратегию 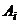называют доминирующей над стратегией 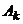(стратегию 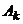называют доминируемой).

Определение 33. Если в платежной матрице элементы 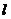-го столбца не больше соответствующих элементов 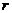-го столбца, то есть 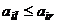( 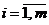), то стратегию 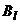называют доминирующей над стратегией 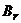(стратегию 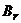называют доминируемой).

Определение 34. Стратег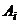ии 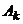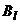и ( и 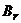) называют дублирующими друг друга, если ( ) ( ( )).

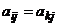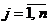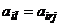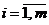Замечание. Дублирование является частным случаем доминирования. Игрокам выгоднее пользоваться доминирующими стратегиями. Поэтому вероятность применения доминируемых стратегий равна нулю. Исключая из платежной матрицы доминируемые стратегии, можно уменьшить ее размерность, что упрощает решение игры. При исключении доминируемых стратегий цена игры не меняется.

Теорема 4. Оптимальные смешанные стратеги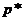и и 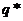в игре с платежной матрицей 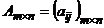и ценой 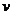остаются оптимальными и для игры с платежной матрицей 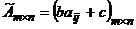( 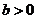) и ценой .

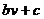На основании теоремы 4 платежную матрицу всегда можно преобразовать так, что ее элементы будут целыми неотрицательными числами, что упрощает расчеты.

Пример 40.6. Найти решение игры, заданной платежной матрицей

.

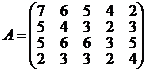Решение. Найдем верхнюю и нижнюю цены игры:

, .

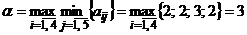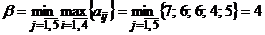Так как 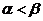, то игра не имеет решения в чистых стратегиях. Оптимальной стратегией первого игрока является стратегия 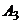, так как в ней расположен максимин 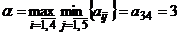. Оптимальной стратегией второго игрока является стратегия 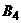, так как в ней расположен минимакс .

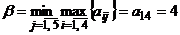Исключим невыгодные стратегии первого игрока. Так как все элементы строки 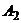не превосходят элементов строки 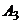, то строку 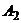можно исключить. Аналогично все элементы строки 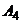не превосходят элементов строки 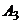, поэтому исключаем 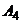. Строку 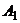исключить нельзя, так как в ней есть элементы, превосходящие элементы строки 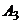. Тогда преобразованная платежная матрица игры будет иметь вид 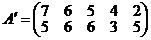. Исключим невыгодные стратегии второго игрока. Все элементы столбцов 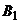, 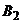и 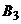больше соответствующих элементов столбца 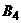, поэтому эти столбцы можно исключить. В столбце 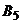есть элементы, меньшие соответствующих элементов столбца 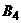, поэтому этот столбец следует оставить. Преобразованная платежная матрица игры будет иметь вид .

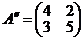Найдем седловую точку матрицы 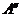в смешанных стратегиях. Пусть смешанные стратегии игроков определяются векторами вероятностей 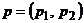, , 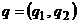компоненты которых удовлетворяют условию нормировки 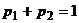, 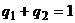. Функция выигрыша будет иметь вид

.

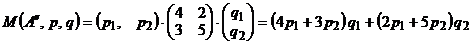Так как первый игрок стремится получить максимальный гарантированный выигрыш 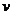, то при оптимальной смешанной стратегии 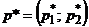должно выполняться равенство 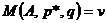или 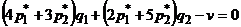. С учетом условий нормировки система уравнений для определения оптимальных стратеги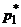й и 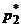первого игрока имеет вид

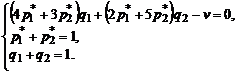
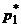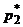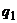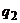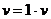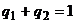В ней содержится 3 уравнения и 5 неизвестных. Для отыскания и исключим переменные и с помощью подстановки: так как и , то 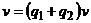. Тогда первое уравнение системы после подстановки в него выражения 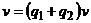и группировки слагаемых относительно 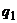и 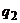можно записать следующим образом: .

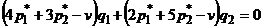Так как по теореме 3 значения 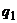и 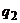должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных 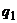и 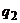только в том случае, когда выполняется равенство 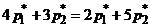. Из условия нормировки 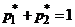выразим 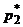и подставим в полученное равенство. Раскрывая скобки и выражая 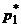, получим 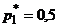, 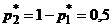. Таким образом, вероятности стратегий первого игрока , .

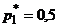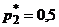Применяя аналогичный прием для отыскания 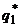и 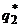получаем, что вероятности стратегий второго игрока , .

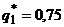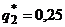Подставим найденные оптимальные смешанные стратегии в функцию выигрыша, найдем цену игры .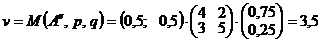

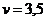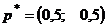Ответ. Цена игры при и 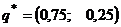. Первый игрок может с одинаковыми вероятностями применять обе стратегии. Второму игроку выгоднее чаще использовать первую стратегию.

40.5. Графический метод решения матричных игр,
не имеющих решения в чистых стратегиях

Для построения решений игр, в которых число стратегий хотя бы одного из игроков равно двум, существует достаточно эффективный графический метод. Будем предполагать, что в рассматриваемых играх нет седловой точки в чистых стратегиях.

Определение 35. Матричную игру, в которой число стратегий первого игрока равно двум, а число стратегий второго игрока равно 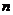, называют 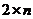-игрой.

Платежная матрица первого игрока 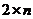-игры имеет вид

.

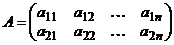Определение 36. Ломаную линию, состоящую из отрезков семейства прямых 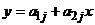( 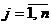) и расположенную не выше каждой прямой семейства, называют нижней огибающей семейства прямых ( ).

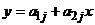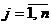Определение 37. Ломаную линию, состоящую из отрезков семейства прямых 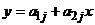( 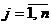) и расположенную не ниже каждой прямой семейства, называют верхней огибающей семейства прямых ( ).

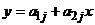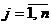Замечание. Нижнюю и верхнюю огибающие семейства прямых будем обозначать соответственно , .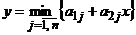

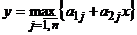Определение 38. Матричную игру, в которой число стратегий первого игрока равно 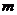, а число стратегий второго игрока равно двум, называют 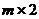-игрой.

Платежная матрица 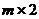-игры имеет вид .

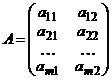Определение 39. Матричную игру, заданную платежной матрицей размерности 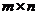называют 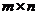-игрой.

Замечание. Если матричную 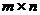игру можно свести к игре 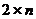или 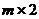, то ее всегда можно решить графическим методом.

Обозначим 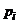– вероятность применения первым игроком стратегии 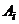, 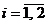; 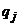– вероятность применения вторым игроком стратегии , , , .

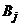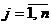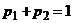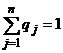Алгоритм графического решения 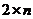-игры

1) Проверить, что игра не имеет решения в чистых стратегиях.

2) Исключить невыгодные стратегии второго игрока, упростить платежную матрицу.

3) На отрезке 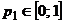построить семейство прямых 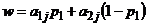( 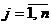), уравнения которых составлены с использованием столбцов упрощенной платежной матрицы 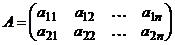и условия нормировки .

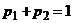4) Построить нижнюю огибающую 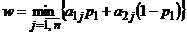, выделить ее высшую точку 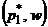и стратегии второго игрока, прямые которых проходят через точку .

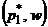5) Найти оптимальные стратегии игроков. В зависимости от формы нижней огибающей может представиться несколько случаев.

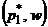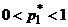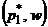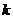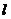Первый случай. Нижняя огибающая имеет ровно одну наивысшую точку , , в точке пересекаются ровно две прямые (например, с номерами и ), соответствующие чистым стратегиям 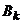и 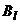второго игрока (рис. 40.1, а)). Для отыскания оптимальной смешанной стратегии первого игрока необходимо выполнить следующие действия:

а) найти координаты точки 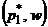как решение системы уравнений, соответствующих чистым стратегиям 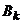и 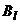второго игрока:

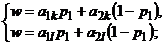
б) найти оптимальную смешанную стратегию первого игрока 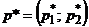, в которой .

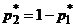Для отыскания оптимальной смешанной стратегии второго игрока необходимо выполнить следующие действия:

а) в платежной матрице оставить только столбцы, соответствующие стратегиям 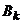и 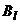второго игрока: ;

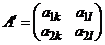б) с использованием строк матрицы 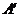составить систему уравнений

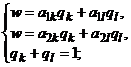
в) найти решение 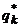и 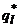полученной системы уравнений;

г) составить оптимальную смешанную стратегию второго игрока, полагая вероятности исключенных стратегий второго игрока равными нулю: .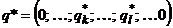

Второй случай. Нижняя огибающая имеет ровно одну наивысшую точку 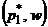, , 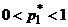в точке 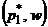пересекается более двух прямых, соответствующих чистым стратегиям второго игрока. Для отыскания оптимальной смешанной стратегии следует выбрать прямые, входящие в нижнюю огибающую (рис. 40.1, б)), а затем провести вычисления, аналогичные первому случаю.

Третий случай. Нижняя огибающая имеет ровно одну наивысшую точку 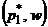, 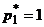. Тогда оптимальной стратегией первого игрока является чистая стратегия 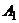, 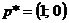. В качестве оптимальной стратегии второго игрока следует выбрать чистую стратегию 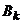, соответствующую прямой с наименьшимположительным наклоном, проходящей через точку 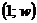(рис. 40.1, в)). Далее следует составить оптимальную смешанную стратегию второго игрока, полагая 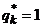, а вероятности остальных стратегий – равными нулю.

Четвертый случай. Нижняя огибающая имеет ровно одну наивысшую точку 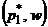и 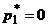. Тогда оптимальной стратегией первого игрока является чистая стратегия 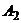, 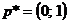. В качестве оптимальной стратегии второго игрока следует выбрать чистую стратегию 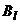, соответствующую прямой с наибольшимотрицательным наклоном, проходящей через точку 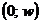(рис. 40.1, г)). Далее следует составить оптимальную смешанную стратегию второго игрока, полагая 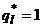, а остальные вероятности равными нулю.

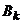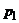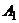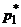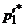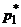Пятый случай. Нижняя огибающая имеет горизонтальный участок, соответствующий чистой стратегии второго игрока (рис. 40.1, д)). Тогда первый игрок имеет бесконечно много оптимальных смешанных стратегий. Вероятность применения первым игроком стратегии может изменяться от до ( и 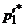– абсциссы точек пересечения прямой, соответствующей чистой стратегии 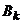, с другими прямыми, образующими нижнюю огибающую). Вероятность 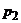применения первым игроком стратегии 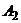может изменяться от 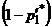до 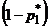. Оптимальной стратегией второго игрока является чистая стратегия 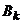, , 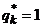вероятности остальных стратегий равны нулю.

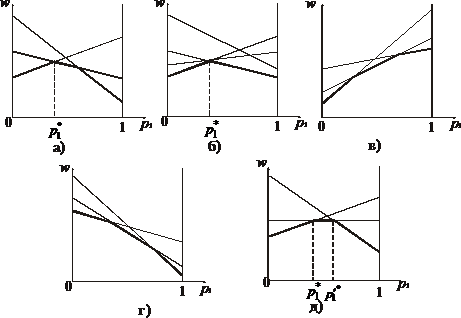
Рис. 40.1

6) Найти цену игры 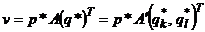. Записать ответ.

Замечание.Выражение 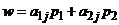характеризует ожидаемый средний выигрыш первого игрока при применении вторым игроком чистой стратегии ( ).

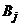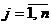Графическое решение 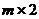-игры во многом аналогично графическому решению 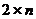-игры, но проходит в другой последовательности.

Алгоритм графического решения 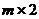-игры

1) Проверить, что игра не имеет решения в чистых стратегиях.

2) Исключить невыгодные стратегии первого игрока, упростить платежную матрицу.

3) На отрезке 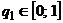построить семейство прямых 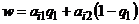( 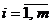), уравнения которых составлены с использованием строк упрощенной платежной матрицы и условия нормировки .

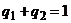4) Построить верхнюю огибающую 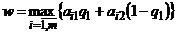, выделить ее низшую точку 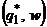и стратегии второго игрока, прямые которых проходят через точку .

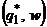5) В платежной матрице оставить только строки, соответствующие стратегиям 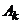и 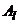первого игрока: .

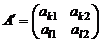6) Найти оптимальные стратегии игроков с использованием верхней огибающей. В зависимости от формы верхней огибающей также может представиться несколько случаев, вычисления в которых проводят аналогично.

7) Найти цену игры по формуле теоремы 3: 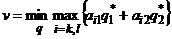. Записать ответ.

Пример 40.7. Найти решение 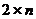-игры, заданной платежной матрицей

.

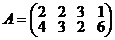Решение. 1) Найдем верхнюю и нижнюю цены игры:

, .

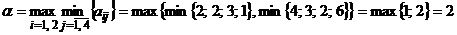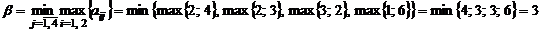Так как 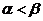, то решения игры в чистых стратегиях нет.

Обозначим 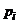– вероятность применения первым игроком стратегии 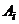, 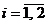; 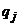– вероятность применения вторым игроком стратегии 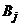, 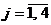. Условия нормировки: , .

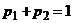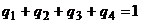2) Упростим платежную матрицу. Заметим, что элементы первого столбца не меньше соответствующих элементов второго столбца. Следовательно, стратегия 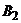является доминирующей над стратегией 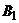. Других доминирующих стратегий в матрице 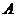нет. Исключим стратегию 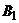, тогда 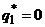. Матрица 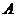примет вид .

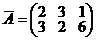3) По столбцам платежной матрицы 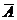с учетом условия нормировки 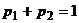составим уравнения семейства прямых 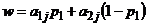( 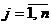), соответствующих чистым стратегиям второго игрока.

Стратегии второго игрока	Ожидаемый средний выигрыш первого игрока	Уравнение прямой

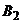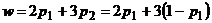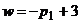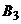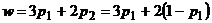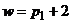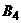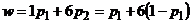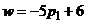Построим полученные прямые на отрезке 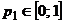(рис. 40.2).

4) Выделим нижнюю огибающую. Из рис. 40.2 видно, что наивысшая точка нижней огибающей лежит внутри интервала 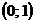и является точкой пересечения прямых 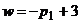и 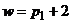, которые соответствуют стратегиям 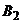и 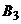второго игрока.

5) Так как нижняя огибающая имеет одну наивысшую точку внутри интервала 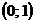, через которую проходят ровно две прямые, соответствующие стратегиям 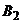и 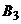, то имеет место первый случай. Найдем оптимальную смешанную стратегию первого игрока:

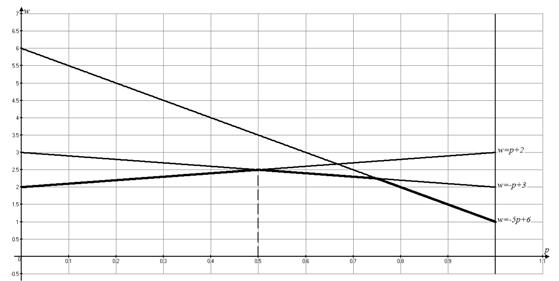
Рис. 40.2

а) найдем точку пересечения прямых 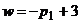и 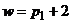: