Фазовая скорость и длина волны.
Под фазовой скоростью волны напряжения или тока понимают скорость перемещения вдоль линии некоторой точки этой волны, которой присуще неизменное фазовое состояние или фазовая скорость υф- скорость с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны напряжения или тока бегущей волны.
Для определения выражения фазовой скорости примем фазу падающей волны (ур.6) неизменной, т.е.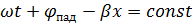 
возьмем производную от этого выражения по времени и приравняем ее к 0.
=> 
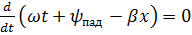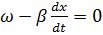
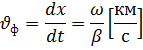
Фазовая скорость одинакова и для падающей и для отраженной волны: у воздушных линий без потерь скорость волны практически равна скорости света. В воздушных линиях с потерями фазовая скорость хотя и немного, то всеже меньше. В кабелях скорость волны в 2-2,5раза меньше(зависит от частоты).
Длиной волны λ называется расстояние между ближайшими двумя точками взятое в направлении распространения волны, фазы колебания в которых различаются на 2π.
Следовательно для падающей волны получим
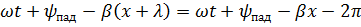
Откуда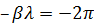 
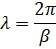
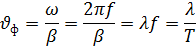
Отсюда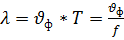 
Т.е за время равное одному периоду Т волна пробегает расстояние, равное длине волны λ.
ПРИМЕР. В воздушных линиях, для для которых скорость волны близко к С0 при f=50Гц длина волны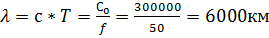 
(длина ЛЭП Волгоград-Москва =1000км- т.е. даже на таких длинных линиях укладывают сравнительно небольшая доля длины волны и нельзя наблюдать волнообразного изменения тока или напряжение вдоль линии, а можно наблюдать лишь их монотонное изменение).
Длина волны λ- наименьшее расстояние между двумя токами имеющими одинаковое фазовое состояние.
Уравнение линии с РП в гиперболических функциях .
Как было показано ранее (§2.3.)напряжение и ток в любой точке сечения линии с РП выражается уравнениями:
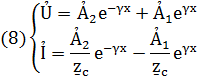
В данных уравнениях комплексные постоянные могут быть определены несколькими способами, если известны граничные условия (либоỦ1 и Ỉ1 в начале, либо Ủ2 и Ỉ2 в конце линии при конкретном режиме работы линии. Рассмотрим 2 наиболее важных, чаще всего встречающихся на практике случаях.
1 случай Ủ1 и Ỉ1 в начале линии (х=0)
Получим из уравнений
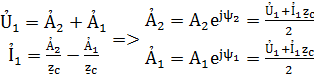
Подставим значения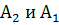 
в исходное уравнение
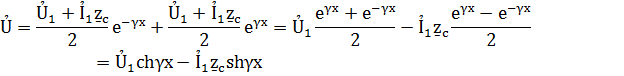
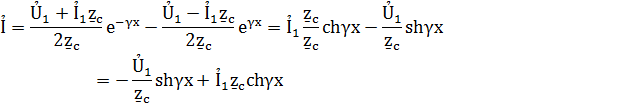
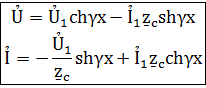
Эти формулы позволяют определить ток и напряжение в любой точке линии о их значениямỦ1 и Ỉ1 в начале линии. Следует отметить чтоchγх иshγх являются комплексными числами, т.к. γх=αх+jβx.
2 случай Ủ2 и Ỉ2 в конце линии (х=0)
При этом можно полагать, что задано сопротивление нагрузки, т.к.
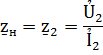
В этом случае удобнее отсчет расстояния вести от конца линии. Примем расстояние до точки от конца линии x’=l-x(где l- длина линии).
При этом имеем
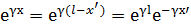
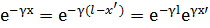
Подставим эти выражения в исходную систему уравнений
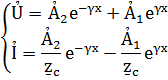
После постановки получаем
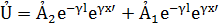
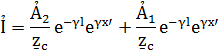
Введем обозначения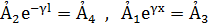 
и получим
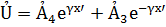
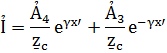
При х’=0 т.е. x=l имеем Ủ=Ủ2 , Ỉ=Ỉ2
Поэтому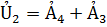 
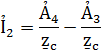
Решаем совместно находим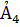 
и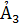 
и подставляем их в исходную систему .
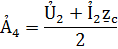
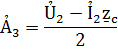
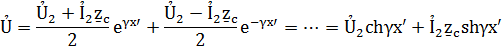
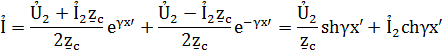
Эти формулы позволяют определить ток и напряжение в любой точке линии по их значениям Ủ2 и Ỉ2 в конце линии