Тема 3 Обратная матрица. Вырожденные и невырожденные матрицы. Обратная матрица и ее вычисление. Матричные уравнения
Пусть A – квадратная матрица.
Матрица B называется обратной к матрице A, если 
Обратная матрица обозначается A-1 и  .
.
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Уравнение вида  называют простейшим матричным уравнением. Если A – квадратная невырожденная матрица, то решением такого уравнения будет матрица
называют простейшим матричным уравнением. Если A – квадратная невырожденная матрица, то решением такого уравнения будет матрица  .
.
Если уравнение имеет вид  , то
, то 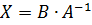 .
.
Пример 1 Найти матрицу обратную данной: 
Решение
1) Найдем определитель матрицы A.

Следовательно, матрица А невырожденная и имеет себе обратную.
2) Найдем алгебраические дополнения к элементам матрицы A.









3) Запишем A-1:
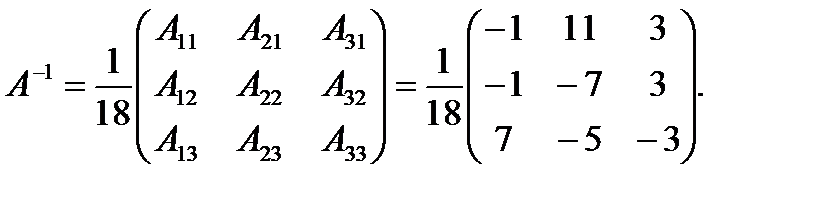
4) Выполним проверку:


Пример 2 Решить матричное уравнение: 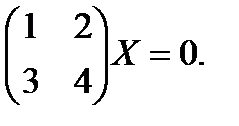
Решение
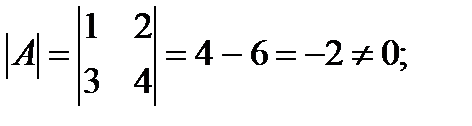
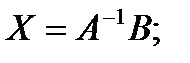


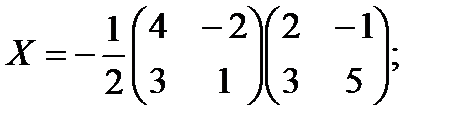

Задачи для решения
1 Найти матрицу, обратную данной:
а)  б)
б)  в)
в)  г)
г) 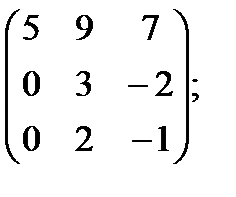 д)
д) 
е)  ж)
ж)  з)
з)  и)
и) 
к)  л)
л)  м)
м)  н)
н) 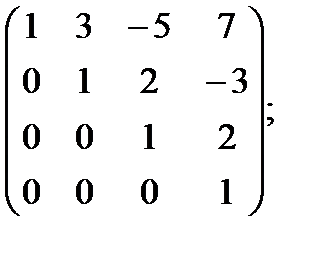
о)  п)
п)  .
.
2 Решите матричное уравнение:
а)  б)
б) 
в)  г)
г) 
д)  е)
е) 
ж)  з)
з) 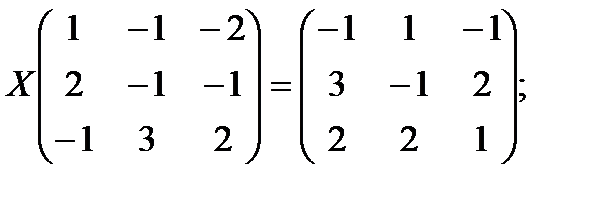
и)  к)
к)  .
.
Раздел 3 Системы линейных уравнений. Методы решения систем линейных уравнений
Тема 1 Решение системы n – линейных уравнений с n неизвестными в матричном виде
Пусть дана система линейных уравнений:
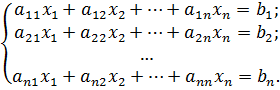
Рассмотрим матрицу, составленную из коэффициентов при неизвестных:

Матрица А коэффициентов при неизвестных называется главной матрицей системы.
Свободные члены и неизвестные можно записать в виде столбцевых матриц:
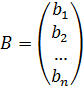
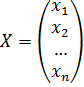
Тогда, используя правило умножение матриц, эту систему уравнений можно записать так:
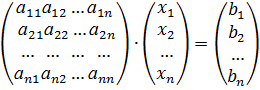
или
A·X = B (1)
Равенство (1) называется матричным уравнением или системой уравнений в матричном виде.
Отсюда
Х =  B.
B.
Таким образом, чтобы решить систему уравнение, нужно:
1) Найти обратную матрицу  .
.
2) Найти произведение обратной матрицы  на матрицу-столбец свободных членов В, т. e. Х =
на матрицу-столбец свободных членов В, т. e. Х =  B.
B.
Пользуясь определением равных матриц, записать ответ.
Пример Решить систему уравнений:

Х =  , B =
, B =  , A =
, A = 
Найдем обратную матрицу А-1.
D =  =
=  5
5  2
2  2 + (-1)
2 + (-1)  3
3  4 + (-1)
4 + (-1)  1
1  3 - ((-1)
3 - ((-1)  2
2  4 + 5
4 + 5  3
3  3 + 1
3 + 1  (-1)
(-1)  2) =
2) =
= 20 - 12 - 3 - (- 8 + 45 - 2) = 5-35 = -30.
 ∙
∙  = - 5; A21 =
= - 5; A21 =  ; A31 =
; A31 = 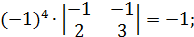
A12 =  A22 =
A22 =  ; A32 =
; A32 =  ;
;
A13 =  ∙
∙ 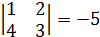 ; A23 =
; A23 =  A33 =
A33 = 
A-1 =  =
= 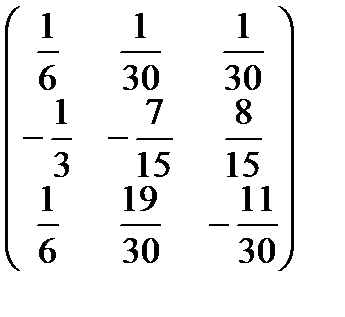 ;
;
Cделаем проверку:
A×A-1 =  =E.
=E.
Находим матрицу Х.
Х =  = А-1В =
= А-1В =  ×
×  =
=  .
.
Проверка:
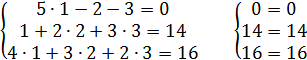 (верно)
(верно)
Решением системы является набор (1, 2, 3): x = 1; y = 2; z = 3.
Задачи для решения
1 Решить системы линейных уравнений матричным методом
а) 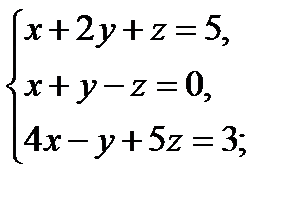 б)
б)  в)
в) 
г) 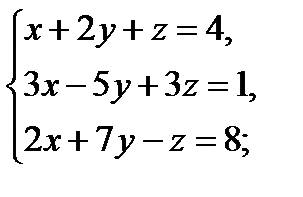 д)
д)  е)
е) 
2 Решить системы линейных уравнений
а) 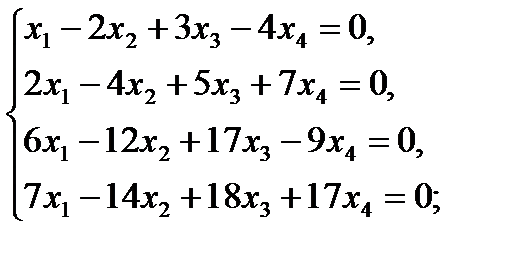 б)
б) 
в)  г)
г) 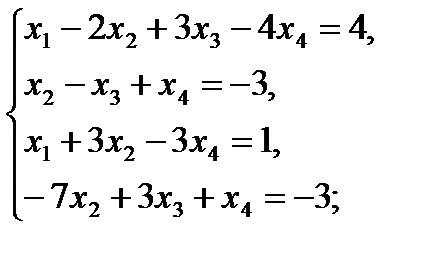
д)  е)
е) 
Тема 2 Правило Крамера
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными
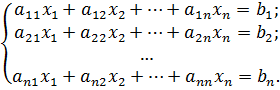
Обозначим через Δ и Δj определитель матрицы системы и определители, полученные из определителя Δ заменой j-го столбца столбцом свободных членов системы:

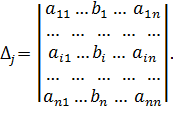
Если определитель матрицы системы отличен от нуля, Δ≠0, то решение системы определяется равенствами:

Пример Решим по правилу Крамера систему трех линейных уравнений с тремя неизвестными.

Запишем матрицу системы, столбец свободных членов и вычислим определитель матрицы системы:
 .
.
Определитель матрицы системы отличен от нуля. Система имеет единственное решение. Вычислим его по формулам Крамера. Для этого найдем определители 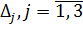 .
.
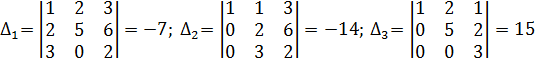 .
.
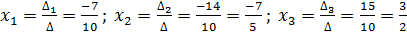 .
.
Проверим:
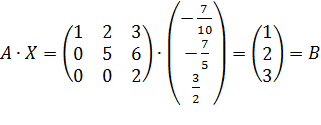 .
.
1 Решить систему линейных уравнений по правилу Крамера:
а) 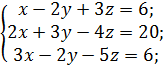 б)
б)  в)
в) 
г)  д)
д) 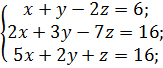 ж)
ж) 
з) 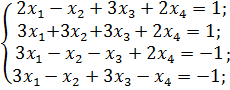 и)
и) 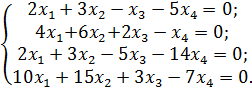
Тема 3 Метод последовательного исключения неизвестных (метод Гаусса)
Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Рассмотрим метод Гаусса на примере системы из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из второго и третьего исключим слагаемые, содержащие 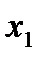 . Для этого второе уравнение разделим на
. Для этого второе уравнение разделим на  и умножим на
и умножим на  , а затем сложим с первым уравнением. Аналогично третье уравнение разделим на
, а затем сложим с первым уравнением. Аналогично третье уравнение разделим на 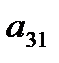 и умножим на
и умножим на 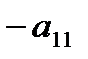 и сложим с первым. В результате исходная система примет вид:
и сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения легко найти  , затем из второго уравнения
, затем из второго уравнения  . Для этого третье уравнение разделим на
. Для этого третье уравнение разделим на  , умножим на
, умножим на  и сложим со вторым. Тогда будем иметь систему уравнений:
и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда легко найти  , затем из второго уравнения
, затем из второго уравнения 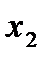 , и из первого
, и из первого 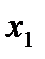 . Вместо того чтобы писать систему уравнений выписывают расширенную матрицу системы, которая состоит из коэффициентов этой системы и свободных членов. Приводим ее к ступенчатому виду.
. Вместо того чтобы писать систему уравнений выписывают расширенную матрицу системы, которая состоит из коэффициентов этой системы и свободных членов. Приводим ее к ступенчатому виду.

Матрица имеет ступенчатый вид, если
· все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками;
· ведущий элемент (первый ненулевой элемент строки при отсчёте слева направо) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.

Цель элементарных преобразований– привести матрицу к ступенчатому (треугольному) виду.
Элементарными преобразованиями матрицы называются следующие ее преобразования:
I Перестановка двух строк матрицы.
II Умножение всех элементов одной строки матрицы на одно и то же число, отличное от нуля.
III Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число.
IV Вычеркивание нулевой строки.
Пример:
Решить методом Гаусса систему уравнений:
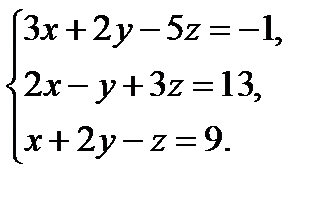
Запишем расширенную матрицу системы: 
Поменяем местами первую и третью строки
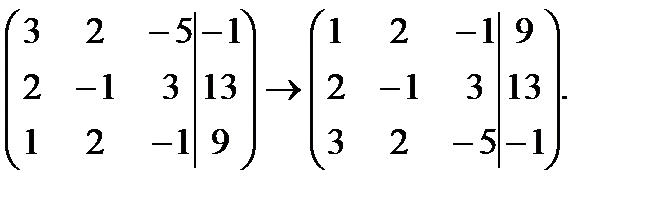
Мы получили единицу в верхнем углу. Теперь нужно получить нули в первом столбце 2-ой и 3-ей строки. Для этого ко второй строке прибавим первую строку, умноженную на -2:
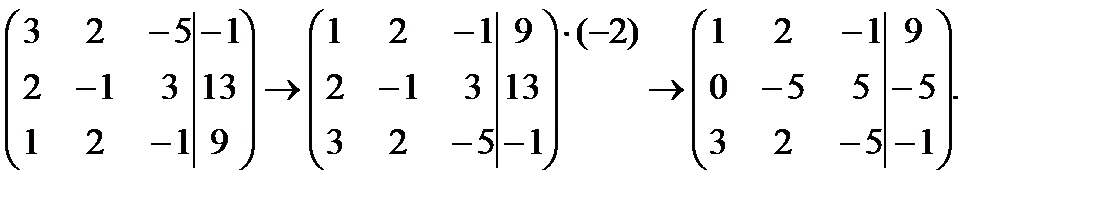
К третьей строке прибавим первую, умноженную на 3:
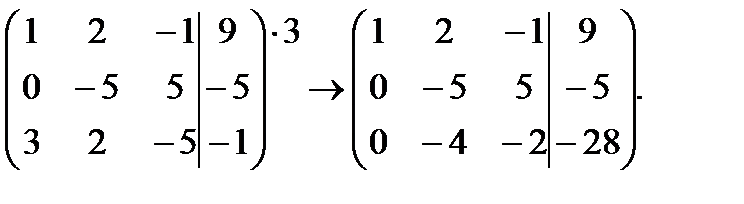
Вторую строку умножим на -1/5, а третью строку на -1/2

К третьей строке прибавим вторую строку, умноженную на -2
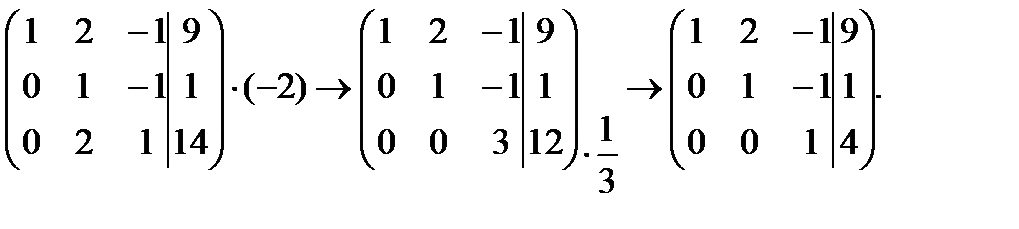
Из последней строчки находим, что  .
.
Из второй строки находим y: 
И из первой строки найдем x: 
Таким образом, мы нашли решение системы:
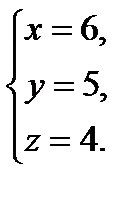
Решить методом Гаусса следующие системы уравнений:
1 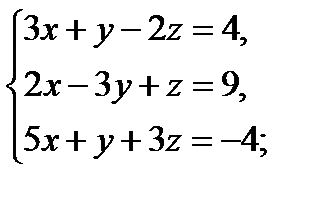 2
2  3
3  4
4 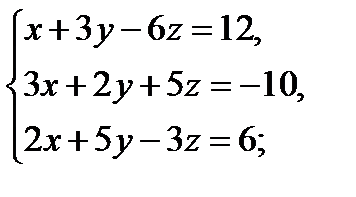
5  6
6  7
7  8
8 
9  10
10 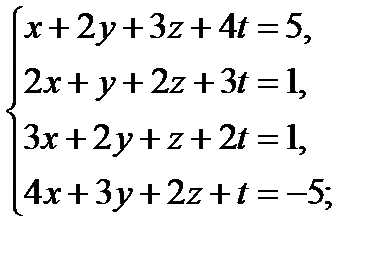 11
11 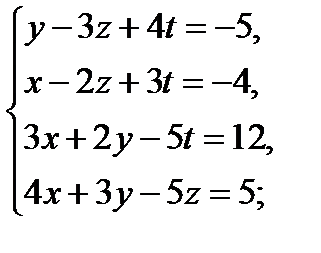
12  13
13 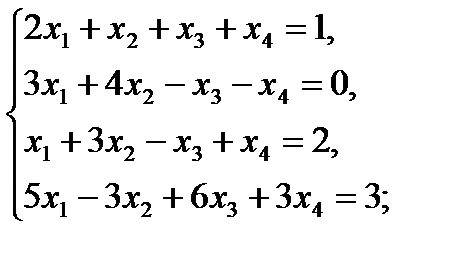 14
14 
15  16
16 
17  18
18 
19 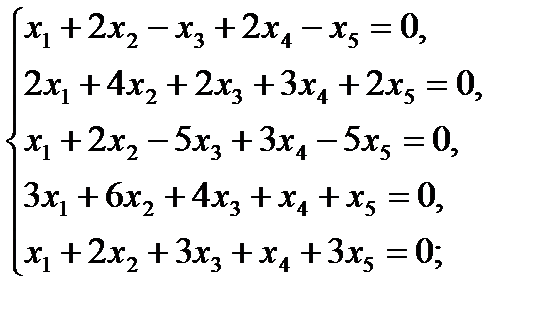 20
20 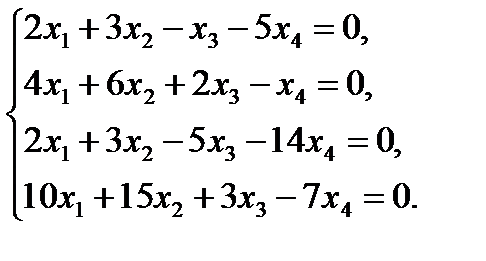
Шатных Олеся Николаевна
АЛГЕБРА
(ЧАСТЬ 1)
Материалы для практических занятий
и самостоятельной работы
для студентов факультета М и ИТ
Редактор
____________________________________________________________________
Подписано к печати Формат бумаги 60  84 1/16 Бумага тип № 1
84 1/16 Бумага тип № 1
Печать цифровая Усл. печ.л. 2,25 Уч.-изд.л.
Заказ Тираж 30 Не для продажи
____________________________________________________________________
РИЦ Курганского государственного университета.
640669, г. Курган, ул. Гоголя, 25.
Курганский государственный университет.
