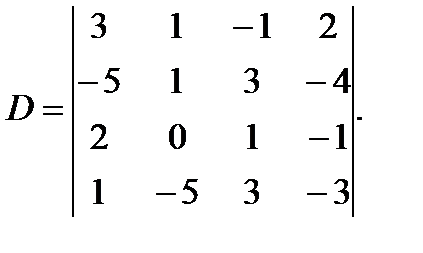Геометрическое решение уравнений
Найти геометрическое решение неравенства 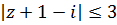 .
.
Решение: 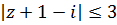 ,
, 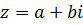 ,
, 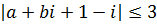 ,
, 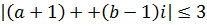 . Найдем модуль комплексного числа
. Найдем модуль комплексного числа 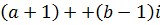 .
.
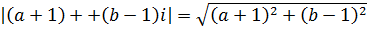 .
.
Получим 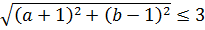 (1), возведем в квадрат правую и левую части (1), получим
(1), возведем в квадрат правую и левую части (1), получим 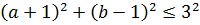 .
.
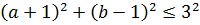 – геометрически это круг с центром в точке A (-1; 1) и радиусом 3 (рисунок 5).
– геометрически это круг с центром в точке A (-1; 1) и радиусом 3 (рисунок 5).
y
-1 0 x
Рисунок 5 – Решение неравенства
Задачи для решения
1 Найти решение систем:
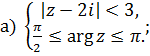
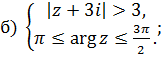
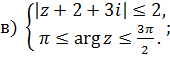
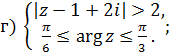
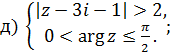
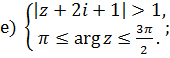
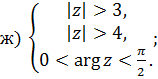
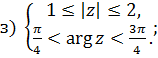
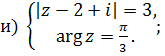
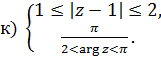
Раздел 2 Матрицы и определители
Тема 1 Матрицы. Определение матрицы, виды матриц, действия над матрицами
Матрицей называется прямоугольная таблица, составленная из чисел некоторого поля 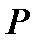 . Числа, из которых состоит матрица, называются элементами матрицы. Если матрица имеет m строк и n столбцов, то (m, n) называют размерностью матрицы.
. Числа, из которых состоит матрица, называются элементами матрицы. Если матрица имеет m строк и n столбцов, то (m, n) называют размерностью матрицы.
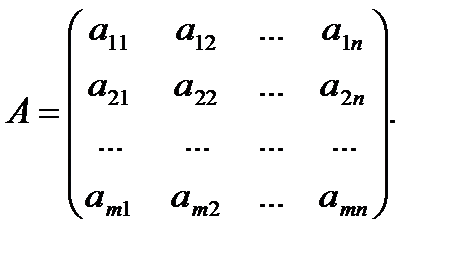
Если число строк матрицы равно числу столбцов, то такая матрица называется квадратной.
Две матрицы называютсяоднотипными, если они имеют одинаковую размерность.
Действия над матрицами
I Суммой матриц A+ Bназывается матрица 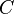 , элементы которой равны суммам соответствующих элементов матриц A и B, т. е. cij = aij + bij.
, элементы которой равны суммам соответствующих элементов матриц A и B, т. е. cij = aij + bij.
Складывать и вычитать можно только матрицы одинаковой размерности (число строк и столбцов у них должно быть одинаково).
Пример 1: 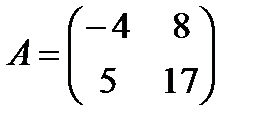 ,
, 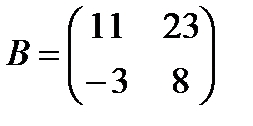 .
.
Решение: 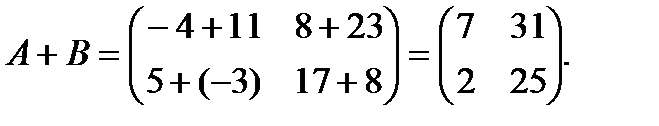
II Произведением матрицы А на число λназывается матрица В, которая получается из матрицы А умножением всех ее элементов на λ, т.е.
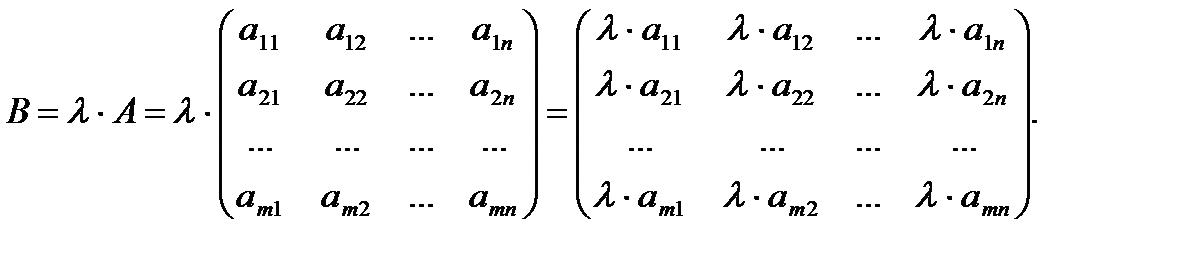
Пример 2: 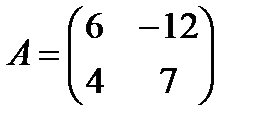 ,
, 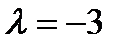 .
.
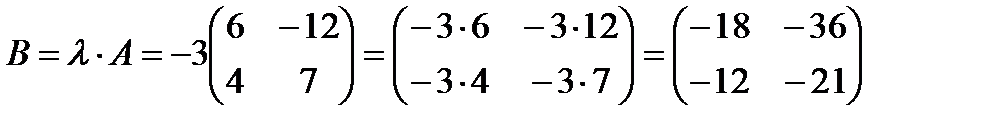 .
.
IIIРазность двух матрицодинаковой размерности можно определить через операцию сложения матриц и через умножение матрицы на число:
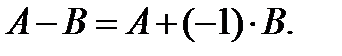
Пример 3: 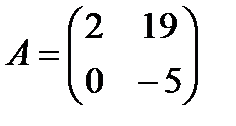 ,
, 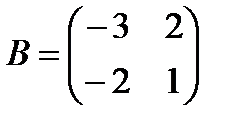 .
.
Решение: 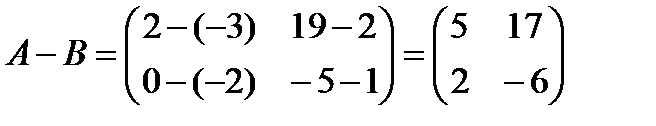 .
.
VIМатрицу 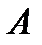 можно умножить на матрицу
можно умножить на матрицу 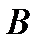 тогда и только тогда, когда число столбцов в первой матрице равно числу строк во второй. При этом получается матрица, имеющая столько строк, сколько в первой, и столько столбцов, сколько во второй.
тогда и только тогда, когда число столбцов в первой матрице равно числу строк во второй. При этом получается матрица, имеющая столько строк, сколько в первой, и столько столбцов, сколько во второй.
Произведением двух матриц 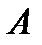 и
и 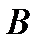 называется матрица
называется матрица 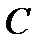 , элементы которой вычисляются по правилу умножения
, элементы которой вычисляются по правилу умножения 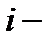 ой строки матрицы
ой строки матрицы 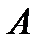 на
на 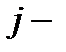 ый столбец матрицы
ый столбец матрицы 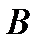 .
.
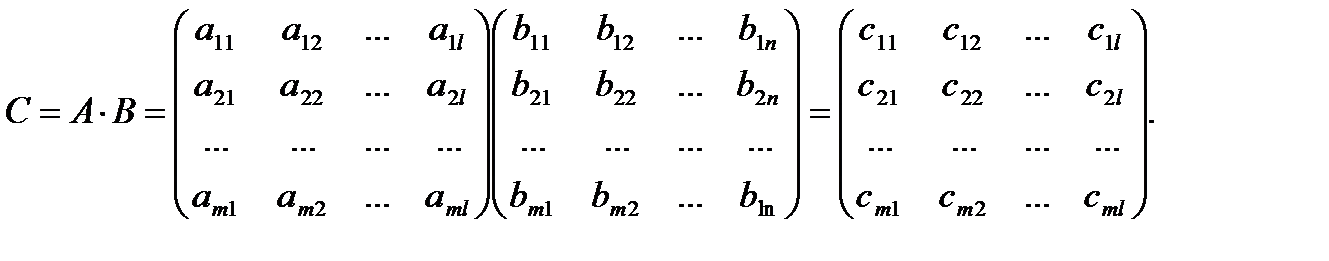
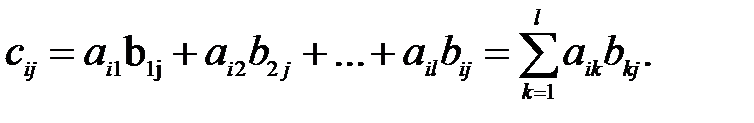
Пример: Умножить матрицу А на матрицу В:
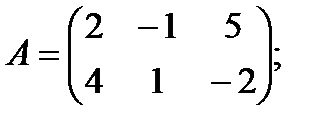
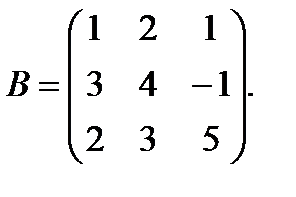
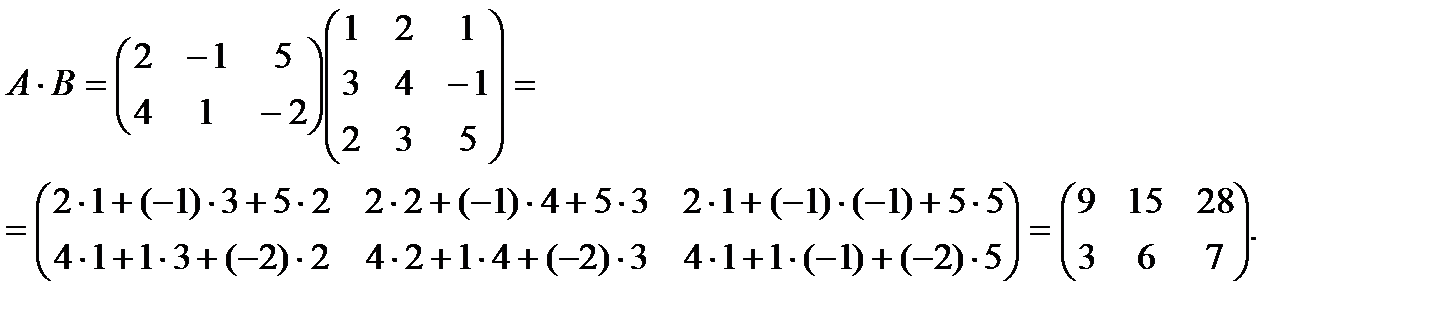
Задачи для решения
1 Найти сумму матриц A и B:
a) 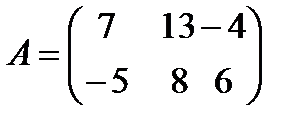 ,
, 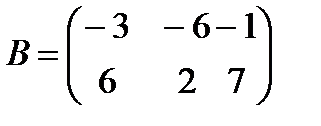 ;
;
б) 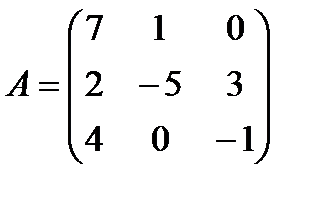 ,
, 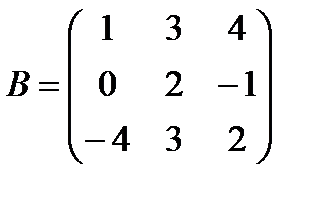 ;
;
в) 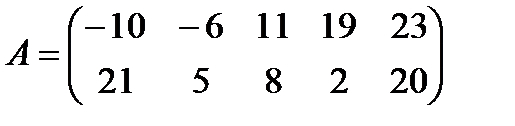 ,
, 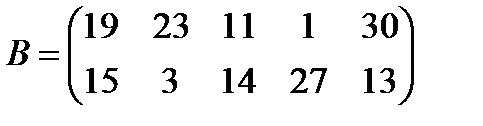 ;
;
г) 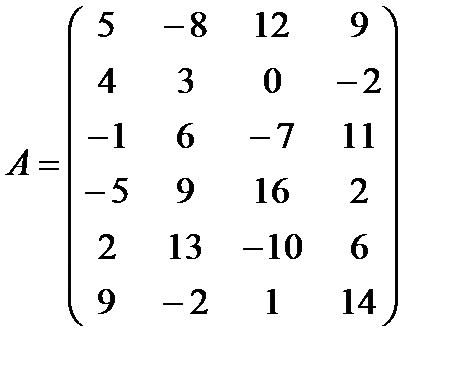 ,
, 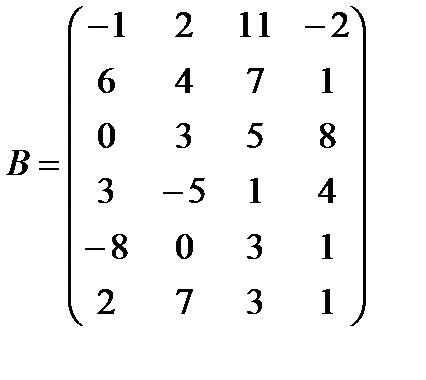 ;
;
д) 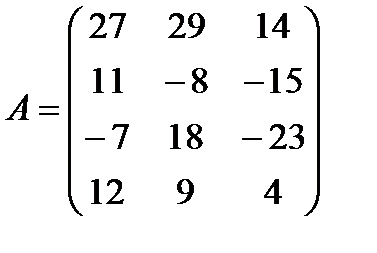 ,
, 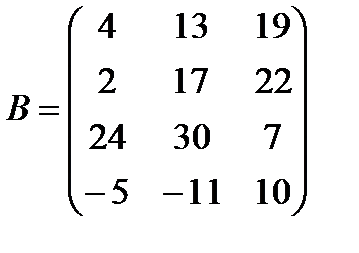 ;
;
е) 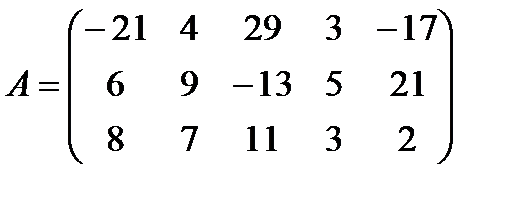 ,
, 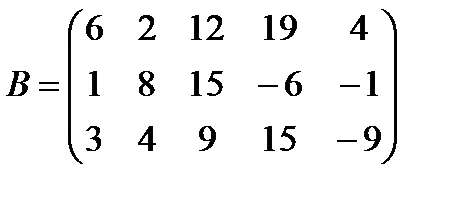 ;
;
2 Умножить матрицу A на число 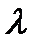 :
:
а) 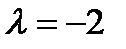 ,
, 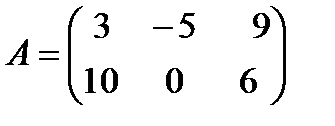 ; б)
; б) 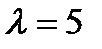 ,
, 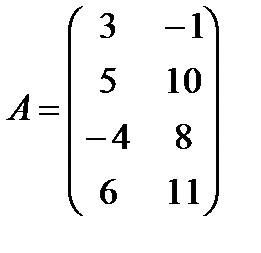 ;
;
в) 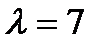 ,
, 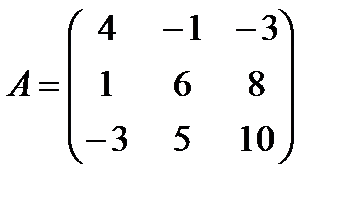 ; г)
; г) 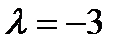 ,
, 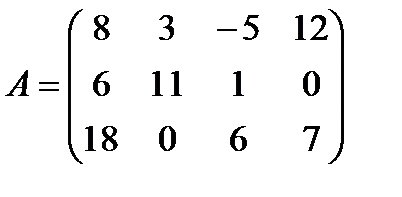 ;
;
д) 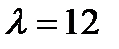 ,
, 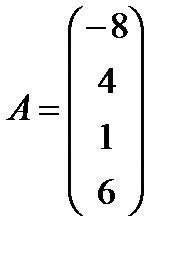 ; е)
; е) 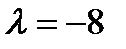 ,
, 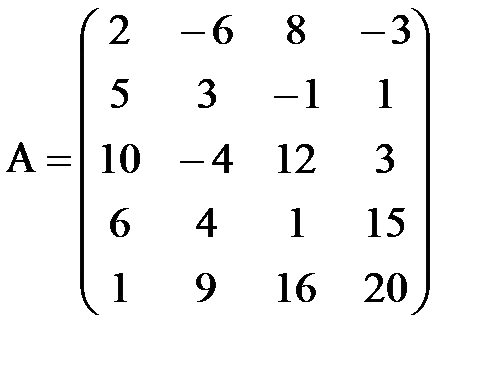 ;
;
3 Найти разность матриц A и B:
a) 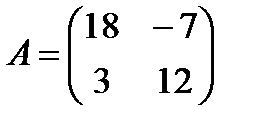 ,
, 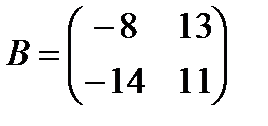 ;
;
б) 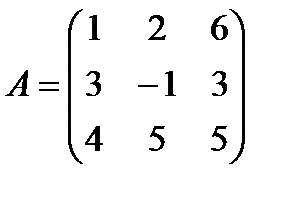 ,
, 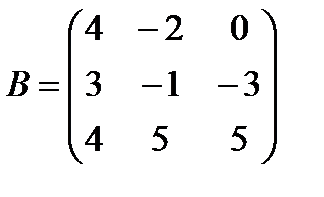 ;
;
в) 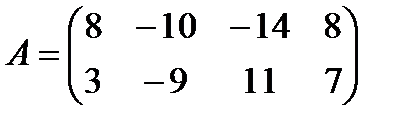 ,
, 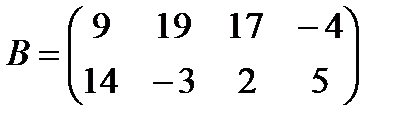 ;
;
г) 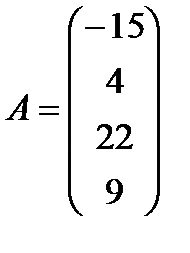 ,
, 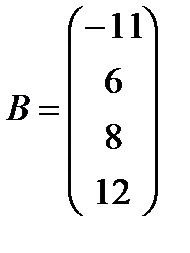 ;
;
д) 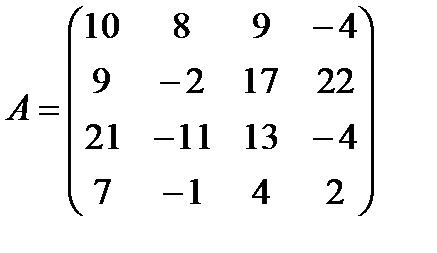 ,
,  ;
;
e) 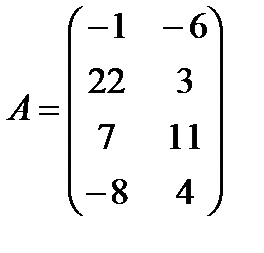 ,
, 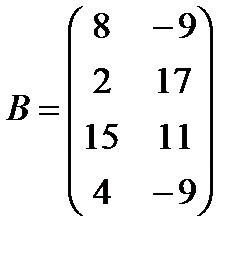 ;
;
4 Найдите произведение матриц A и B:
a) 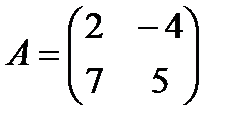 ,
, 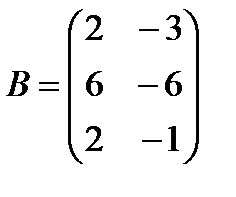 ;
;
б) 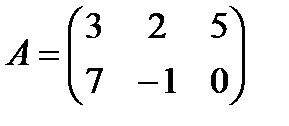 ,
, 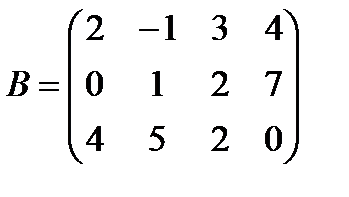 ;
;
в) 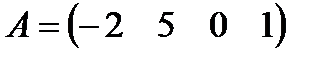 ,
, 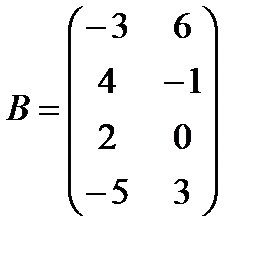 ;
;
г) 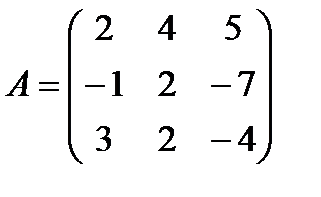 ,
, 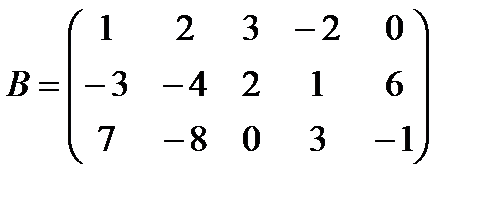 ;
;
д) 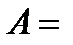
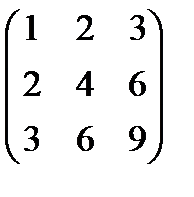 ,
, 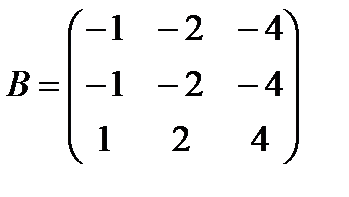 ;
;
е) 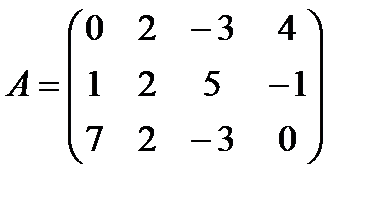 ,
, 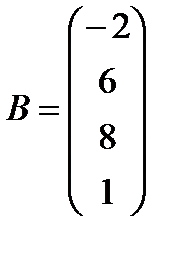 .
.
5 Даны матрицы:
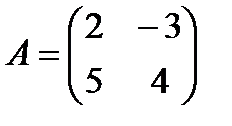 ,
, 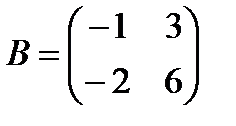 ,
, 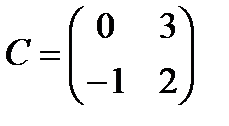
Найти: а) 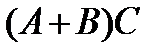 ; б)
; б) 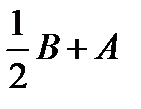 ; в)
; в) 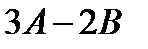 ; г)
; г) 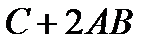 ;
;
д) 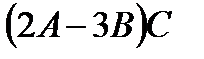 ; е)
; е) 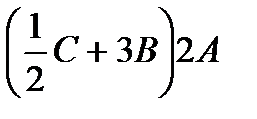 ;
;
6 Выполните действия:
а) 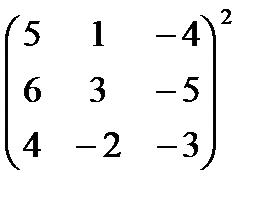 ;
;
б) 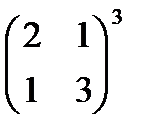 ;
;
в) 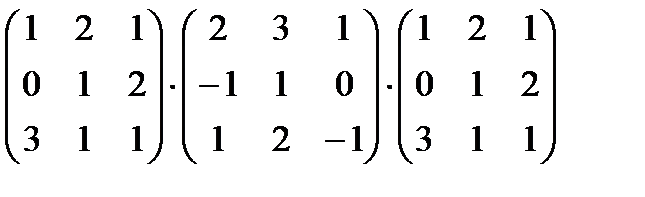 ;
;
г) 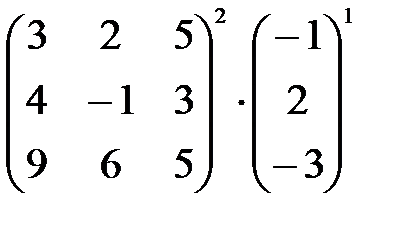 ;
;
д) 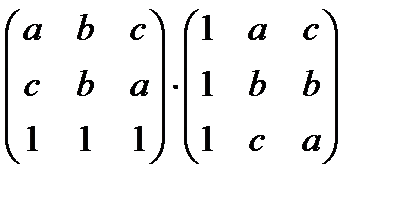 ;
;
е) 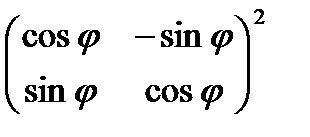 .
.
7 Найти значение многочлена 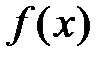 от матрицы А:
от матрицы А:
а) 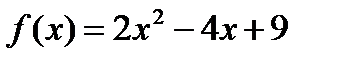 ;
; 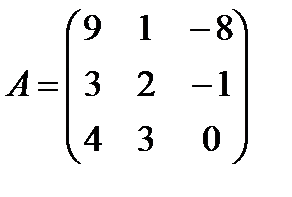 ;
;
б) 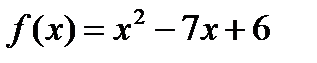 ;
; 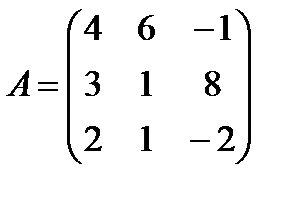 .
.
Тема 2 Определители. Перестановки из n элементов. Подстановки n-ой степени. Определение определителя n-го порядка. Свойства определителей. Миноры и алгебраические дополнения. Теорема о разложении определителя по элементам строки или столбца. Следствие из неё
Перестановкой чисел 1, 2, ..., n называется любое расположение этих чисел в определенном порядке. Число всех перестановок, которые можно образовать из n чисел, равно 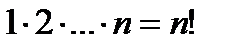 .
.
Если в некоторой перестановке мы поменяем местами какие-либо два символа, а все остальные символы оставим на месте, то мы получим новую перестановку. Это преобразование перестановки называется транспозицией. Инверсию образуют два числа в перестановке, когда меньшее из них расположено правее большего.
Каждой перестановке можно сопоставить число инверсий в ней, которое подсчитывается следующим образом: для каждого из чисел определяют количество стоящих правее его меньших чисел, и полученные результаты складываются.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Произвольное взаимно-однозначное отображение множества первых 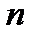 натуральных чисел на себя называется подстановкой
натуральных чисел на себя называется подстановкой 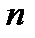 -го порядка. Подстановка может быть записана с помощью двух перестановок.
-го порядка. Подстановка может быть записана с помощью двух перестановок.
Пример перестановки: (1 2 3 4) 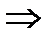 (2 4 1 3);
(2 4 1 3);
Пример транспозиции: (12 3 4) 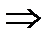 (4 2 3 1);
(4 2 3 1);
Пример инверсии: перестановка (2 4 1 3) содержит три инверсии элементов 2 и 1, 4 и 1, 4 и 3.
Задачи для решения
1 Указать транспозиции, с помощью которых можно
а) от перестановки (10 1 2 8 7 4 3 6 9 5) перейти к перестановке (8 9 5 1 10 7 2 3 6 4)
б) от перестановки (9 5 1 8 3 7 4 6 2) перейти к перестановке (9 8 7 6 5 4 3 2 1)
в) от перестановки (2 4 6 … 2n 1 3 5… 2n-1) перейти к перестановке (2n 2n-1…. 4 3 2 1).
2 Найти число инверсий в следующих перестановках
а)( 8 1 5 9 7 4 3 6 2);
б) (10 5 3 8 4 7 2 6 1 9);
в) музыка, если в качестве исходной принимается перестановка букв (а з к м у ы).
Определителем n-го порядканазывается алгебраическая сумма n! членов, составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причем член берется с плюсом, если его индексы составляют четную подстановку, и со знаком минус - в противоположном случае.
Пусть дана квадратная матрица А второго порядка 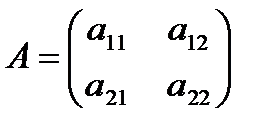 .
.
Определитель квадратной матрицы А второго порядка равен числу  . Диагональ
. Диагональ 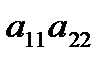 – главная,
– главная, 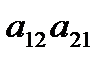 – побочная.
– побочная.
Пусть дана квадратная матрица А третьего порядка 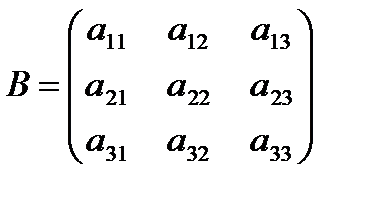 .
.
Определителем квадратной матрицы А третьего порядка называется число, равное
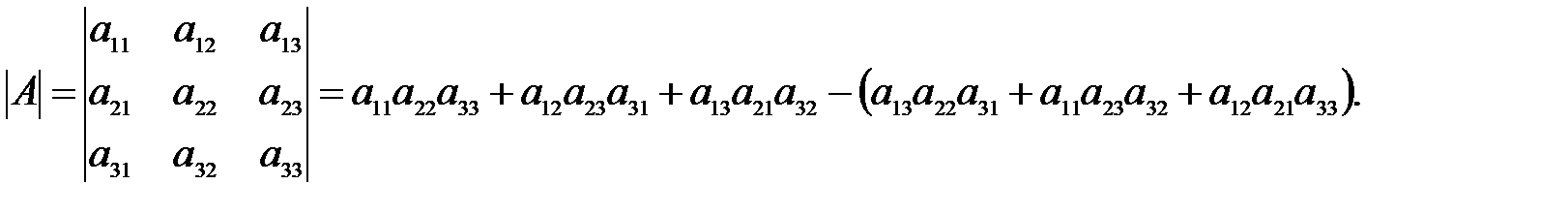
Минором 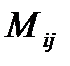 называется определитель, полученный из исходного вычеркиванием
называется определитель, полученный из исходного вычеркиванием 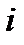 -ой строки и
-ой строки и 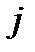 -го столбца.
-го столбца.
Число 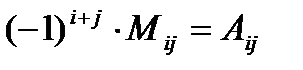 называется алгебраическим дополнением к элементу aij.
называется алгебраическим дополнением к элементу aij.
Теорема 1 (разложение определителя по строке или столбцу):
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения.
Теорема 2:Сумма произведений элементов некоторой строки квадратной матрицы А на алгебраические дополнения соответствующих элементов другой строки равна нулю.
Теорема 100: Определитель, в котором все элементы одной из строк (столбцов), кроме одного, равны нулю равен произведению этого ненулевого элемента на его алгебраическое дополнение.
Пример 1 Найти определитель матрицы A:
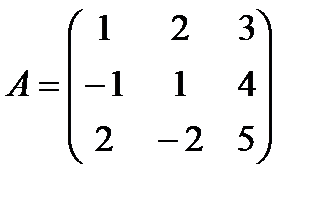
Решение:
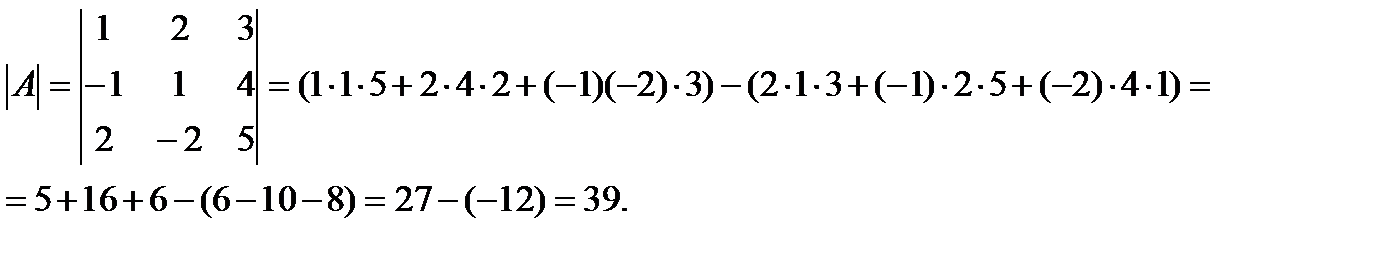
Задачи для решения
1 Найдите определитель 2-го порядка:
а) 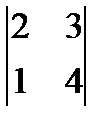 ; б)
; б) 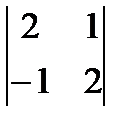 ; в)
; в) 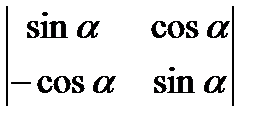 ; г)
; г) 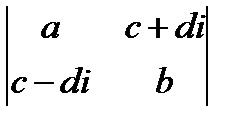 ;
;
д) 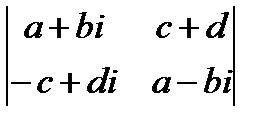 ; е)
; е) 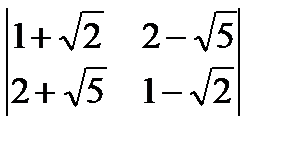 .
.
2 Найдите определитель 3-го порядка:
а) 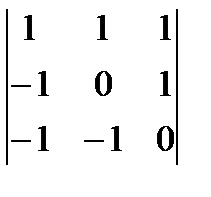 ; б)
; б) 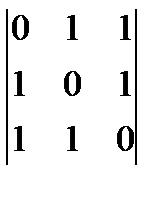 ; в)
; в) 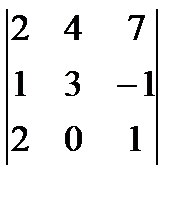 ;
;
г) 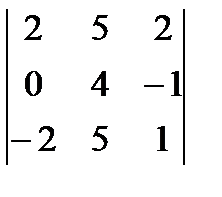 ; д)
; д) 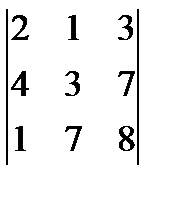 ; е)
; е) 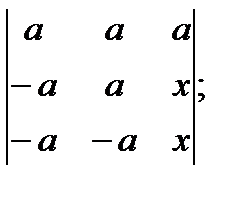
ж) 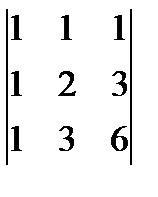 ; з)
; з) 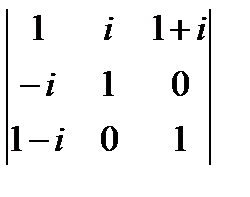 ; и)
; и) 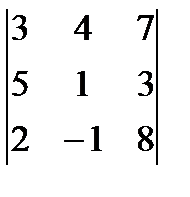 ;
;
к) 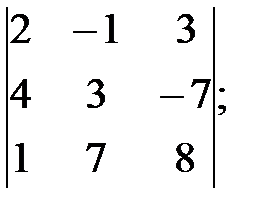 л)
л) 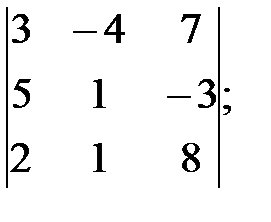 м)
м) 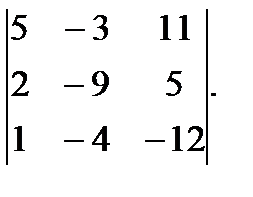
3 Найдите определитель 4-го порядка:
а) 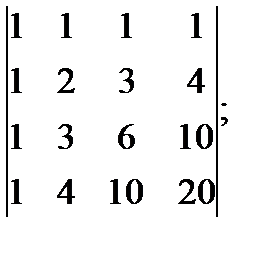 б)
б) 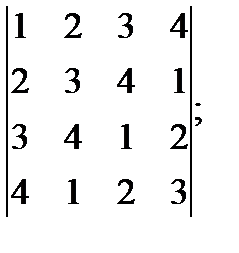 в)
в) 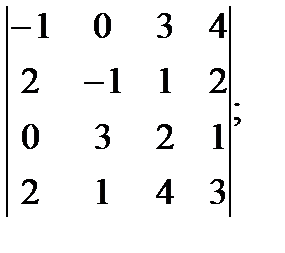 г)
г) 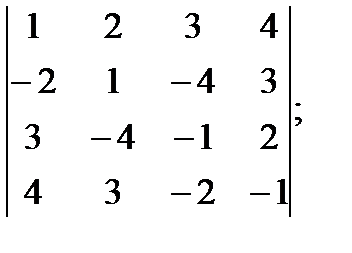
д) 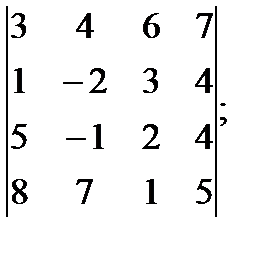 е)
е) 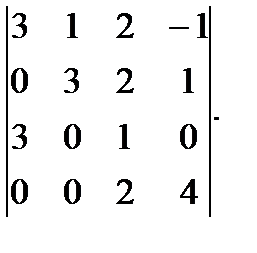
4 Найдите определитель 5-го порядка:
а)  б)
б)  в)
в) 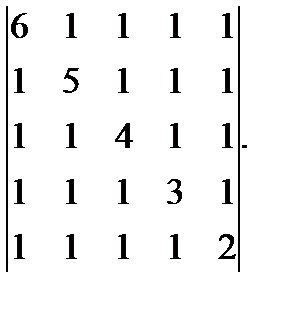
5 Решите уравнения, пользуясь соответствующими свойствами определителя (не применяя правило Саррюса):
а) 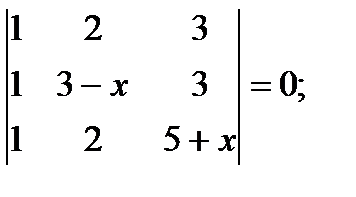 б)
б) 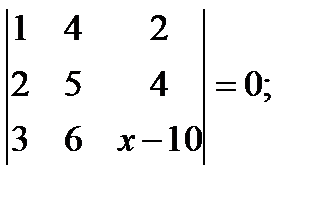 в)
в) 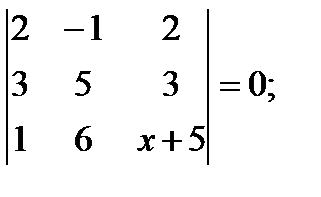
г) 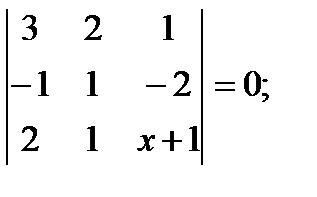 д)
д) 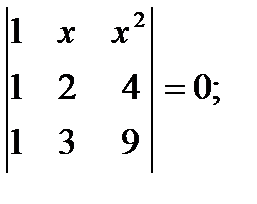 е)
е) 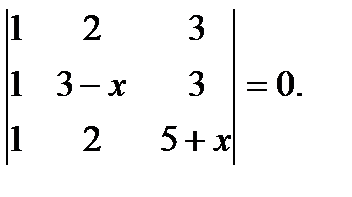
6 Вычислить определители, разложив их по элементам строки (столбца), содержащей буквы:
а) 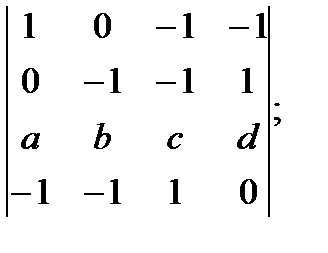 б)
б) 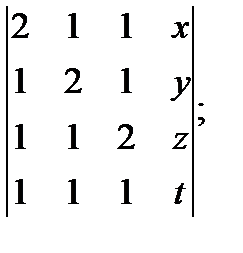 в)
в) 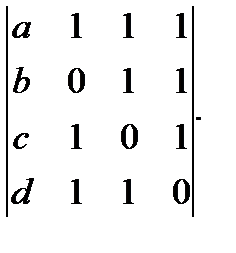
7 Путем разложения по элементам третьей строки вычислить:
а) 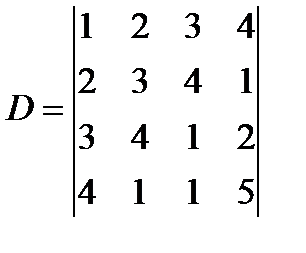 ; б)
; б) 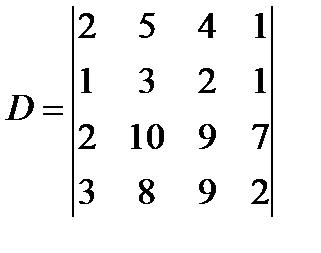 ; в)
; в)