Геометрическое решение задачи

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению расчетно-графической работы по курсу «САПР строительства»
для студентов и магистрантов строительных специальностей

Решение оптимизационных задач строительного производства
методами линейного программирования

Брянск – 2011

Составитель: доцент кафедры Механика Швачко С.Н.

Рецензент: профессор кафедры СП Кожухар В.М.

Рекомендованы учебно-методической комиссией строительного факультета

Протокол № 7 от 12.02.11

Содержание

Содержание. 3

1. Задача о выпуске продукции при ограниченных ресурсах. 4

1.1. Основные понятия. 4

1.2. Условие задачи. 5

1.3. Геометрическое решение задачи. 5

1.4. Решение задачи симплексным методом. 7

1.5. Решение задачи с помощью MS Excel 8

1.6. Решение задачи в системе MathCAD.. 10

2. Транспортная задача. 11

2.1. Основные понятия. 11

2.2. Условие задачи. 12

2.3. Решения задачи методом потенциалов. 12

2.4. Решение задачи с помощью MS Excel 15

2.5. Решения задачи в системе MathCAD.. 16

Литература. 18

Задача о выпуске продукции при ограниченных ресурсах

Основные понятия

Математическое программирование занимается изучением экстремальных задач и методов их решения. В общем случае постановка задачи математического программирования состоит в нахождении экстремального (наибольшего или наименьшего) значения функции целевой функции F(x₁, x₂, … x_n), при системе ограничений g_j(x₁, x₂, … x_n) ≤ b_j , j = 1, 2, … m.

Если F и g_i – линейные функции, то соответствующая задача математического программирования называется задачей линейного программирования (ЗЛП).

Основная задача линейного программирования – нахождение неотрицательного решения системы m уравнений с n неизвестными (система ограничений)

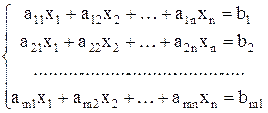
при котором целевая функция F = c₁x₁ + c₂x₂ … + c_nx_n принимает экстремальное (максимальное или минимальное) значение.

Если ранг этой системы r = n, то система имеет единственное решение, которое является оптимальным. Если r < n, то система имеет бесчисленное множество решений. В этом случае r – n неизвестных объявляют свободными (им присваивают произвольные значения), а остальные r неизвестных выражают через свободные.

Любое неотрицательное решение системы ограничений называется допустимым решением или допустимым планом. План, при котором целевая функция F принимает максимальное значение, называется оптимальным планом.

Переменные входящие только в одно уравнение системы с единичным коэффициентом называется базисным. Допустимое решение X при котором свободные переменные равны нулю, а базисные переменные неотрицательны, называется опорным базисным решением.

Множество решений задачи линейного программирования является выпуклым множеством, то есть образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план.

Условие задачи

Бригада рабочих выполняет ремонт квартир и офисов. В состав бригады входят рабочие трех специальностей: плиточники, штукатуры, маляры. Нормы времени работы каждого рабочего в час, необходимые для выполнения ремонта каждого помещения, а также ресурсы рабочего времени для каждого рабочего каждой специальности известны и при­ведены в таблице.

Помещение	рабочие	Прибыль, у.е.
плиточники	штукатуры	маляры
Квартира
Офис
Ресурс времени, чел-дн

Бригада получает прибыль от выполнения одного ремонта квартиры в размере 30 у.е. и одного офиса – в размере 40 у.е. Требуется определить план работ каждого вида, при котором время работы рабочих не превышало бы допустимого ресурса и была получена наибольшая общая прибыль.

Геометрическое решение задачи

Математическая модель задачи звучит следующим образом: среди всех неотрицательных решений системы линейных неравенств

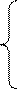12x₁ + 4х₂ ≤ 300,

4х₁ + 4х₂ ≤ 120,

3х₁ + 12х₂ ≤ 252,

x₁, х₂ ≥ 0.

требуется найти такое, при котором функ­ция F = 30x₁ + 40х₂ принимает максимальное значение.

Построим область допустимых решений. Для этого, заменяя знаки неравенств в системе ограничений на знаки равенств, строим соответствующие прямые.

Для построения каждой прямой достаточно найти положение двух точек.

12x₁ + 4х₂ = 300; x₁ = 0, x₂ = 75; x₂ = 0, x₁ = 25.

4х₁ + 4х₂ = 120; x₁ = 0, x₂ = 30; x₂ = 0, x₁ = 30.

3х₁ + 12х₂ = 252; x₁ = 0, x₂ = 21; x₂ = 0, x₁ = 84.

Каждая прямая разбивает плоскость на две полуплоскости. Чтобы определить знак неравенства для полуплоскости, из нее берется какая-то контрольная точка и ее координаты подставляем в соответствующее неравенство. Например, возьмем точку О (0; 0) и подставим ее координаты в неравенство 12x₁ + 4х₂ ≤ 300. Получим 0 < 300, неравенство справедливо и, следовательно, полуплоскость определяемая этим неравенством содержит точку О (0; 0). Отметим эту полуплоскость. Аналогично находим области решения второго и третьего неравенств. Объединяя области решений неравенств, видим, что областью допустимых решений является многоугольник OABCD.

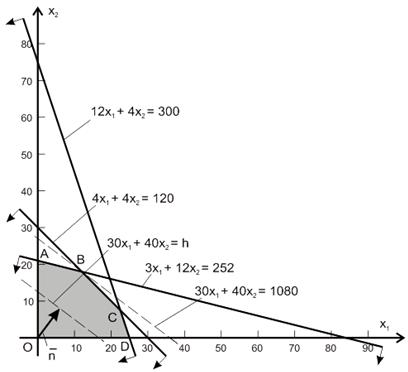
Рисунок 1.1 – Графическое решение задачи линейного программирования

Из начала координат построим вектор grad F = 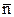= {30, 40}, указывающий направление наискорейшего возрастания функции F.

Построим линии уровня целевой функции F = 30x₁ + 40х₂ = h. Положим h = 500. Соответствующая линия уровня будет: 30x₁ + 40х₂ = 500. Пусть x₁ = 0, x₂ = 12,5; x₂ = 0, x₁ = 16,67.

Передвигая линии уровня целевой функции в направлении вектора 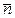, видим, что максимальное значение функция F принимает в точке B.

Решения систему уравнений:

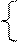4х₁ + 4x₂ = 120,

3x₁ + 12x₂ = 252,

получим х₁^* = 12, x₂^* = 18. Сле­довательно, если бригада выполнит ремонт 12 квартир и 18 офисов, то получит максимальную прибыль, рав­ную F_max = 30∙12 + 40∙18 = 1080 у.е.